병합적 군집분석 (AgglomerativeClustering)의 linkage 옵션은 다음과 같다.
| Linkage | 이상치 민감도 | 특징 |
| Single | 낮음 | 길게 연결된 클러스터 |
| Complete | 낮음 | 조밀한 클러스터, 멀리 떨어진 점 고려 |
| Average | 중간 | 균형 잡힌 처리 |
| Ward | 높음 | SSE 최소화, 조밀한 클러스터 |

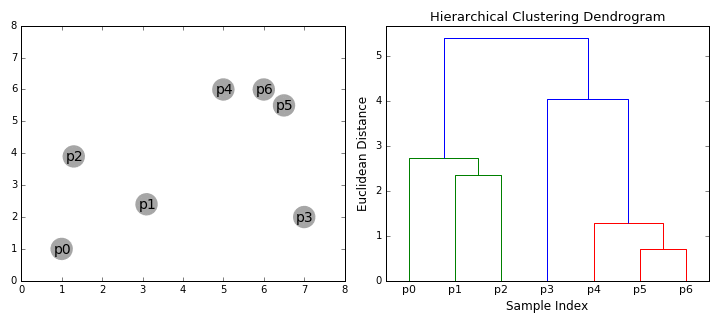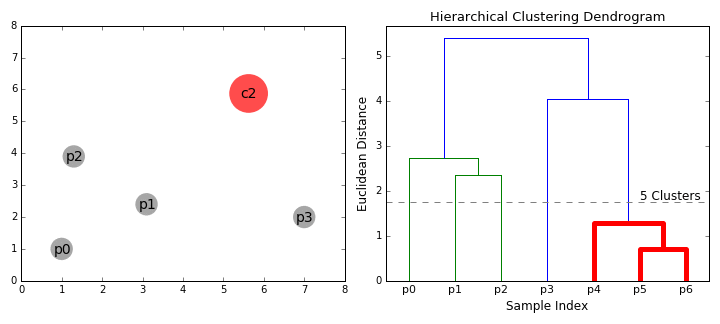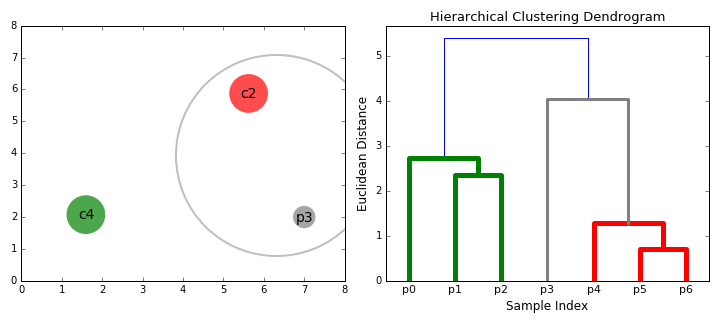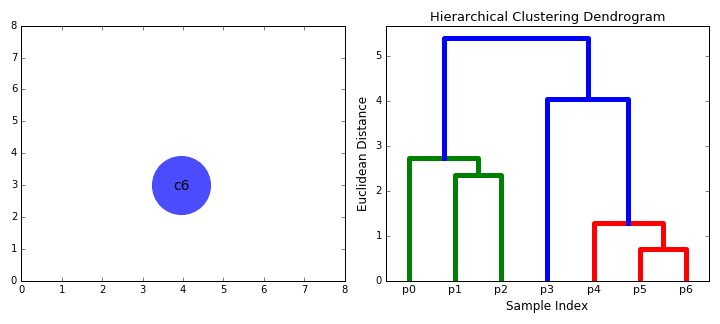
Single linkage (최단거리)
- 두 클러스터 사이의 가장 가까운 두 점의 거리를 클러스터 간 거리로 사용
- 군집 간의 연결을 비교적 좁은 범위에서 연결
장점
- 이상치나 노이즈가 클러스터에 큰 영향을 덜 받음
- 체인 모양(clusters forming chains) 구조를 잘 잡음
단점
- 체인 효과(chain effect): 길게 늘어진 형태의 클러스터가 생김
- 구 모양의 클러스터에는 부적합
적합한 데이터
- 점들이 선형 또는 연결된 형태로 퍼져 있는 경우
Complete linkage (최장거리)
- 두 클러스터 사이의 가장 먼 두 점의 거리를 클러스터 간 거리로 사용
장점
- 구 모양의 조밀한(cluster compact) 클러스터 형성
- 이상치에 덜 민감
단점
- 이상치가 있으면 클러스터 합치기가 지연될 수 있음
- 체인 구조 데이터를 잘 못 잡음
적합한 데이터
- 서로 멀리 떨어진, 조밀한 구형 클러스터를 찾고 싶을 때
Average linkage (UPGMA)
- 두 클러스터 간 모든 점 쌍의 평균 거리를 사용
장점
- 완전 / 단일 linkage의 극단적 문제를 완화
- 구형 / 연결형 데이터 모두 어느 정도 처리 가능
- 이상치 영향을 상대적으로 적게 받음
단점
- 계산 비용이 조금 높음
- 극단값(아웃라이어)에 민감할 수 있음
적합한 데이터
- 클러스터 모양이 불규칙적일 때 균형 잡힌 결과
Ward linkage
- 클러스터 내 제곱합(SSE, sum of squared errors, 분산의 증가량)을 최소화하는 방향으로 병합
장점
- 가장 조밀한 구형 클러스터 생성
- 이상치가 적은 데이터에서 좋은 성능
단점
- 이상치에 민감
- 비구형 데이터에는 부적합
적합한 데이터
- 클러스터 크기가 비슷하고 구형 형태인 경우
다음과 같은 distance_matrix에 대해 군집분석을 적용해 보자.
[0, 1, 4, 6, 8],
[1, 0, 5, 7, 9],
[4, 5, 0, 2, 3],
[6, 7, 2, 0, 1],
[8, 9, 3, 1, 0]Single linkage (최단거리)
- 두 클러스터 간 최소 거리 기준
단계별 병합
- 가장 작은 거리: 0–1 = 1 → merge C0 & C1 → C01 = {0,1}
- 가장 작은 거리: 3–4 = 1 → merge C3 & C4 → C34 = {3,4}
- 가장 작은 거리: C2–C34 = min(2–3=2, 2–4=3) → 2–3=2 → merge C2 & C34 → C234 = {2,3,4}
- C01–C234 = min(0–2=4,0–3=6,0–4=8,1–2=5,1–3=7,1–4=9) → 4 → merge C01 & C234 → {0,1,2,3,4}
Complete linkage (최장거리)
- 두 클러스터 간 최대 거리 기준
단계별 병합
- 가장 작은 최대 거리: 3–4 = 1 → merge C3 & C4 → C34 = {3,4}
- 다음 최소 최대 거리: 0–1 = 1 → merge C0 & C1 → C01 = {0,1}
- 다음 최소 최대 거리: C2–C34 = max(2–3=2,2–4=3) → 3 → merge C2 & C34 → C234 = {2,3,4}
- C01–C234 = max(0–2=4,0–3=6,0–4=8,1–2=5,1–3=7,1–4=9) → 9 → merge C01 & C234 → {0,1,2,3,4}
Average linkage
- 두 클러스터 간 모든 쌍의 평균 거리 기준
단계별 병합 계산
- 초기 거리 평균 = 원래 행렬 사용
- 가장 작은 평균 거리: 0–1 = 1 → C01 = {0,1}
- 가장 작은 평균 거리: 3–4 = 1 → C34 = {3,4}
- C2–C34 평균 거리 = (2–3 + 2–4)/2 = (2+3)/2 = 2.5 → merge C2 & C34 → C234 = {2,3,4}
- C01–C234 평균 거리
= (0–2+0–3+0–4+1–2+1–3+1–4)/6 = (4+6+8+5+7+9)/6 = 39/6 = 6.5 → merge → {0,1,2,3,4}
Ward linkage
- SSE(제곱합) 증가 최소 기준 → 병합 시 cluster 내 분산 증가 최소
단계별 병합
Ward는 구체적인 SSE 계산이 필요하지만, 일반적으로 거리 기반 대략적 단계는 Average linkage와 비슷하게 병합
- 0–1, 3–4 먼저 병합 (거리/분산 최소)
- 그 다음 C2–C34 병합
- 마지막 C01–C234 병합
import numpy as np
import matplotlib.pyplot as plt
from scipy.cluster.hierarchy import linkage, dendrogram
from scipy.spatial.distance import squareform
# 주어진 distance matrix
dist_matrix = np.array([
[0, 1, 4, 6, 8],
[1, 0, 5, 7, 9],
[4, 5, 0, 2, 3],
[6, 7, 2, 0, 1],
[8, 9, 3, 1, 0]
])
# condensed form (linkage 함수에 넣을 수 있는 1차원 거리 벡터)
condensed = squareform(dist_matrix)
labels = ["A", "B", "C", "D", "E"]
methods = ["single", "complete", "average", "ward"]
plt.figure(figsize=(12, 8))
for i, method in enumerate(methods, 1):
plt.subplot(2, 2, i)
Z = linkage(condensed, method=method)
dendrogram(Z, labels=labels)
plt.title(f"Linkage: {method}")
plt.tight_layout()
plt.show()
'개발 > Python' 카테고리의 다른 글
| DecisionTree Hyper Parameters and Attributes (0) | 2025.09.08 |
|---|---|
| 검정 통계량 T, 평균의 차이와 신뢰구간 (0) | 2025.09.08 |
| XGBoost Hyper Parameters and Attributes (0) | 2025.09.08 |
| 군집화 비교 (0) | 2025.09.08 |
| MAE / MAPE / MSE / RMSE / MSLE / R2 (0) | 2025.09.08 |



댓글