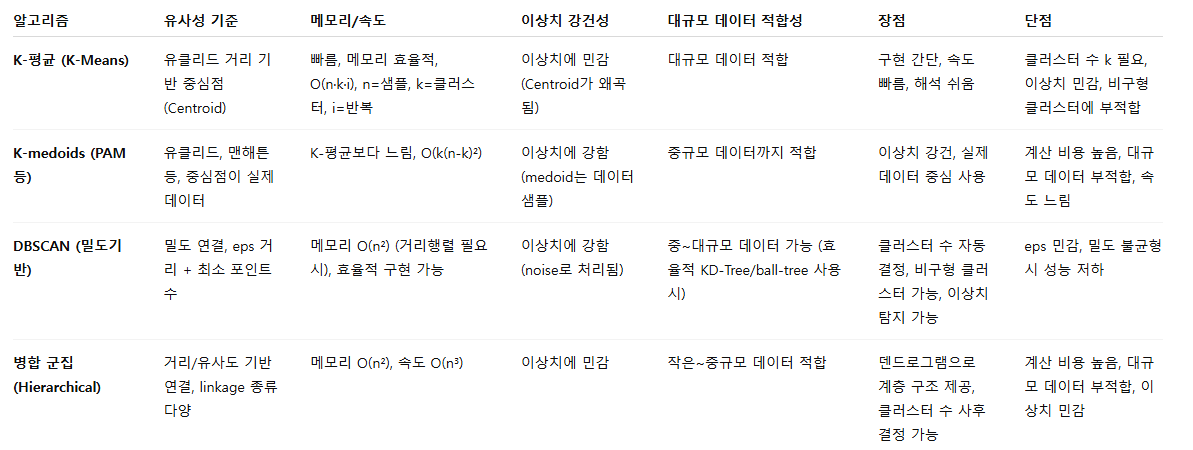
N = 데이터의 수, M = Feature의 수, K = 클러스터 수

실루엣 계수
- 각 데이터 포인트의 군짐 내 응집도와 군집 간 분리도를 기반으로 계산
- 내가 속한 군집 안에서는 얼마나 가깝고, 다른 군집과는 얼마나 멀리 떨어져 있나?
- [-1, 1], 1에 가까울수록 잘 분리, -1이면 잘못된 군집
- 군집이 비구형(non-convex)일 때 성능 나쁨

Dunn Index
- 군집 내 거리의 최소값을 분자, 군집 간 거리의 최대값을 분모로 계산
- 가장 가까운 두 군집은 얼마나 멀고, 가장 넓은 군집은 얼마나 좁은가?
- 값이 클수록 좋음
- 분자(군집 간 최소 거리)는 커야 하고 분모(군집 내부 최대 거리)는 작아야 함
- 이상치에 민감하고 계산이 불안정

Calinski–Harabasz Index (Variance Ratio Criterion)
- 군집 간 분산 대비 군집 내 분산 비율
- 비율이 클수록 품질이 높다.
- ANOVA(분산분석) 개념과 매우 유사
- 보통 최적 K 찾기에 많이 사용 (K-means에서 자주 사용)

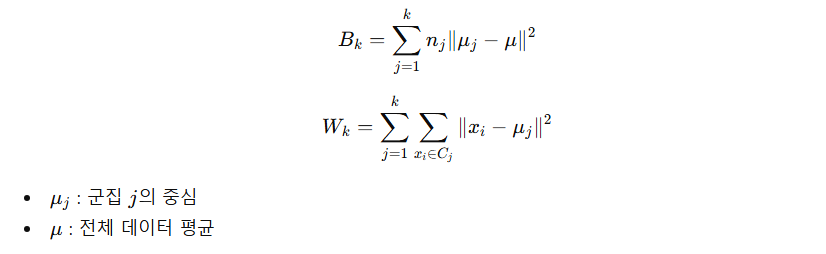
Davies–Bouldin Index (DB Index)
- 군집들이 서로 얼마나 겹치는가?
- 값이 작을수록 좋음
- 군집 간 거리는 커야 하고 군집 내부 산포는 작아야 함
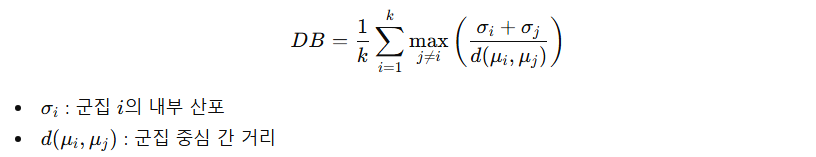
Gap Statistic
- 최적 k 찾기
- 우리 데이터의 군집 구조가 무작위 데이터보다 얼마나 강한가?
- Gap이 가장 커지는 k를 선택

Elbow Method
- WCSS가 급격히 줄어들다 완만해지는 지점 = 최적 k

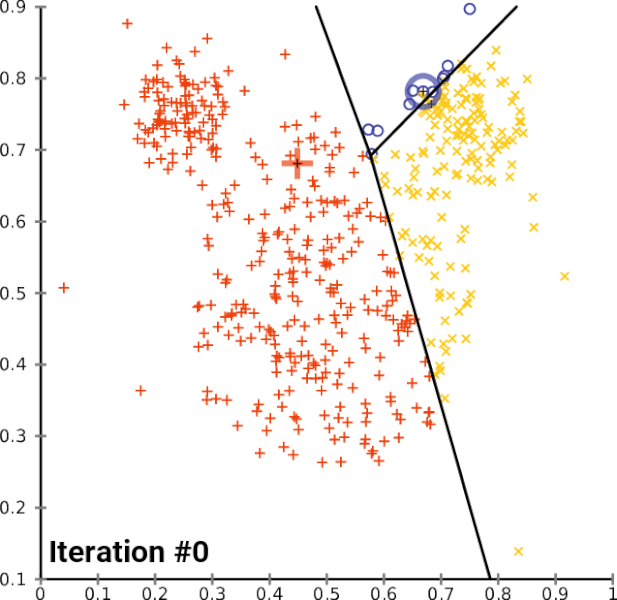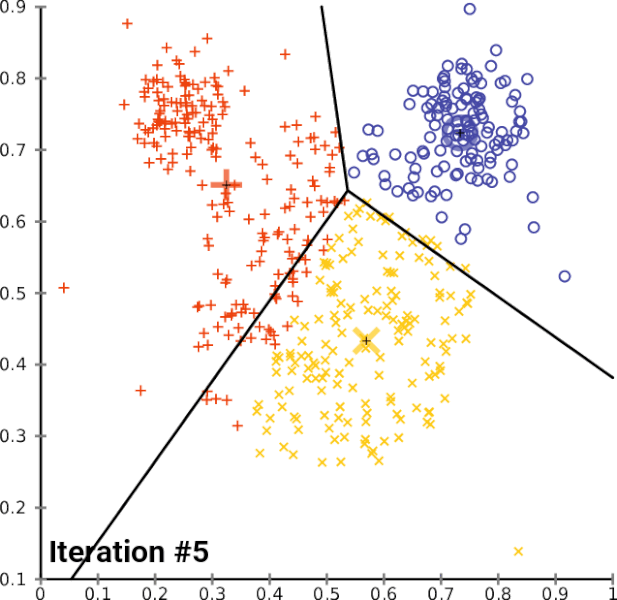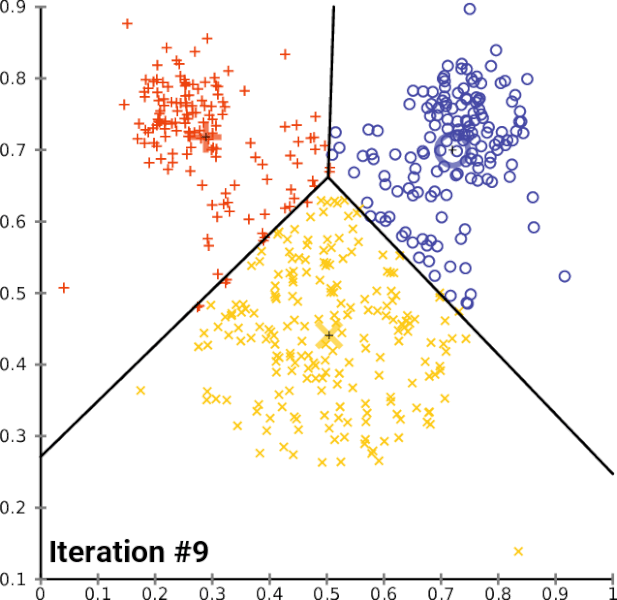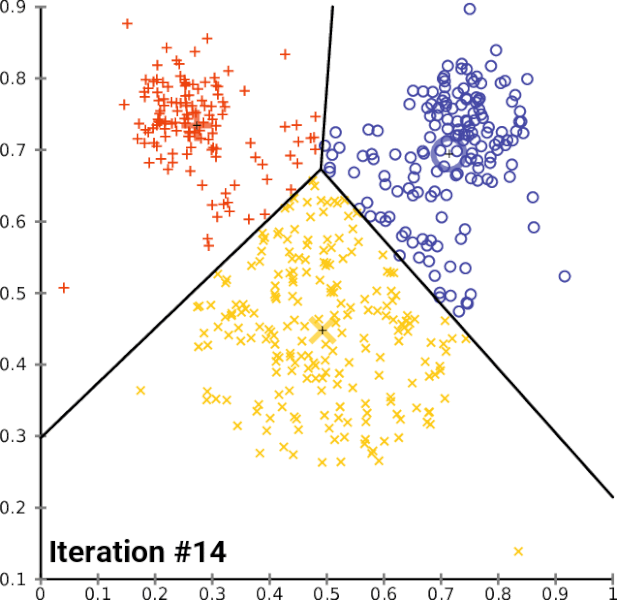
K-Means
- 최적 솔루션을 위해 여러 번 알고리즘을 실행해야 한다. (최초 시작은 random)
- 클러스터 개수 설정이 필요, 스케일링 필요
- distortion function(데이터 포인트와 중심점 간의 거리 제곱 합)을 줄이는 방향으로 갱신
- 이상치에 민감, 데이터간 밀도차가 존재하는 경우 결과가 잘 나오지 않는다. (+ 적절하지 못한 초기치)
- 속성의 개수가 많을 경우 군집화 정확도 감소 (PCA 보완)
- 원형이 아니거나 밀집도가 서로 다른 데이터에서는 잘 작동하지 않는다.
ㄴ 타원형 클러스터는 K-Means보다 가우스 혼합 모델이 적합
PAM (Partitioning Around Medoids)
- 중심 대신 실제 데이터 포인트(메도이드)를 대표점으로 사용하는 기법
- K-Means가 이상치에 민감한 단점을 보완

DBSCAN
- ε 내에 샘플이 최소 min_samples 이상 존재한다면 핵심 샘플로 간주
- 핵심 샘플의 이웃에 있는 모든 샘플은 동일한 클러스터
- 이웃에 다른 핵심 샘플이 있는 경우 추가로 클러스터를 형성
- 핵심도 아니고 이웃도 아닌 샘플은 이상치
- 새로운 샘플에 대해 클러스터를 예측할 수 없음
- 클러스터 간의 밀집도가 크게 다르거나 저밀도 영역이 적은 경우 성능 저하
- 대규모 데이터 셋에 비적합

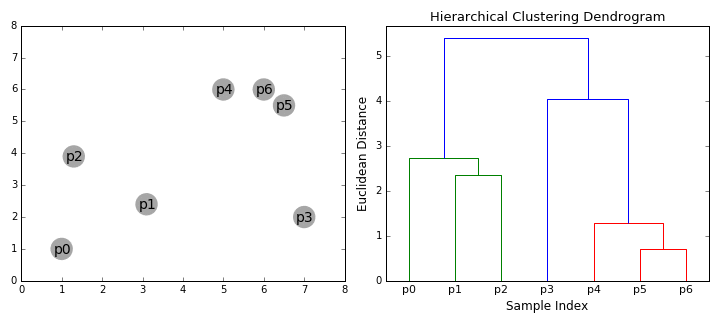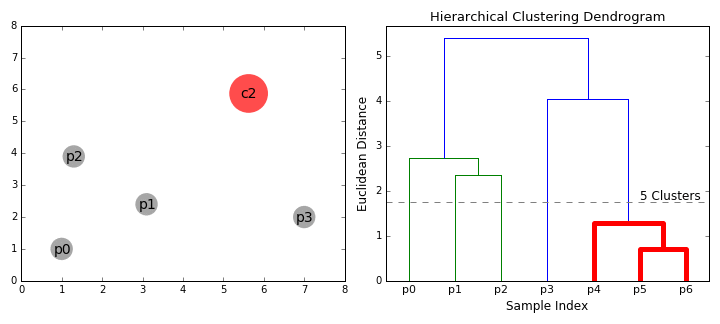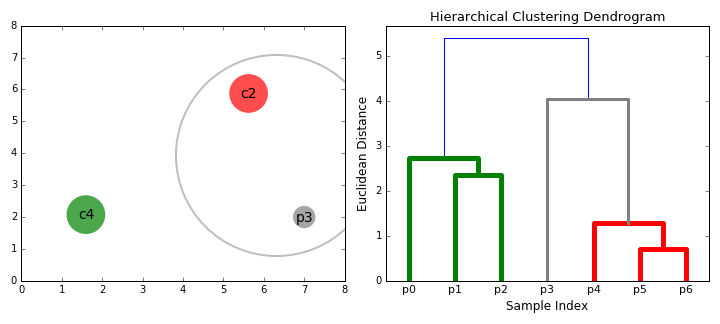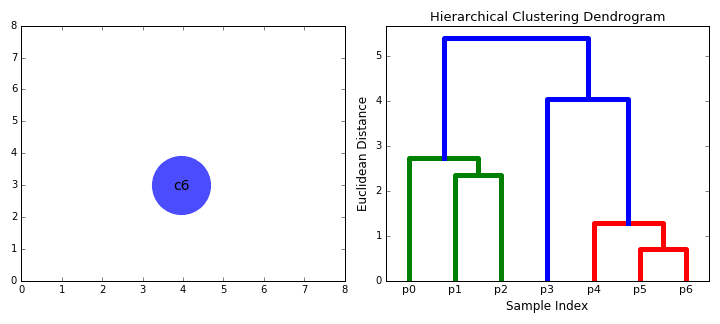
병합 군집 (Agglomerative Clustering)
- 대규모 데이터 셋에 적용 가능
- 연산량이 다른 모델에 비해 큰 편
- 병합 과정 완료 후, 군집의 수를 설정할 수 있음
- 동일한 결과 보장
BIRCH
- Balanced Iterative Reducing and Clustering using Hierarchies
- 대규모 데이터 셋을 위한 알고리즘
- 특성 개수가 많지 않은 경우 K-Means보다 빠름
- 훈련 과정에서 새로운 샘플을 클러스터에 할당하는 트리 구조를 만듬

Mean Shift (평균 이동)
- 각 샘플을 중심으로 원을 그린 후, 원 안에 포함된 샘플의 평균을 구해서 중심을 이동
- 중심이 이동하지 않을 때까지 반복
- 내부 밀집도가 불균형할 때 클러스터를 여러 개로 나눔
- 데이터 분포도를 이용해 군집 중심점을 찾음 (확률 밀도 함수 이용)
- KDE (Kernel Density Estimation)을 이용해서 확률 밀도 함수를 찾음
- 대규모 데이터 셋에 비적합
- 대역폭 크기에 따라 군집화 성능이 달라짐

KDE
- 커널 함수를 통해 어떤 변수의 확률 밀도 함수를 추정하는 방법
- 대역폭 = h이 좁으면 뾰족한 KDE를 가지고 과적합하기 쉬움 (작을수록 세분화돼어 군집화, 라벨의 종류가 많아진다.)
- 대역폭이 크면 평활화된 KDE를 가지고 과소적합하기 쉬움

가우스 혼합 모델 (GMM, Gaussian Mixture Model)
- GMM은 데이터가 여러 개의 가우시안 분포(정규분포)가 섞여서 만들어졌다고 가정
- 군집화를 적용하고자 하는 데이터가 여러 개의 가우시안 분포를 가진 데이터 집합들이 섞여서 생성된 것이라고 가정
- 데이터가 유한한 개수의 타원 모양 클러스터로 그룹되어 있다고 가정 → 샘플이 어느 클러스터에 속한지는 모름
- 즉, 데이터 전체 분포 = 여러 개의 (평균과 분산이 다른) 가우시안 분포들의 가중 합(Mixture).
- AIC, BIC로 적절한 클러스터 개수를 선택


모수 추정
- 개별 정규 분포의 평균과 분산
- 각 데이터가 어떤 정규 분포에 해당되는지의 확률
- GMM은 K-Means와 달리 군집의 중심 좌표를 구할 수 없다. (확률적 중심 좌표 제공)
- KMeans보다 유연한 데이터 세트에 적용 가능, 수행 시간이 오래 걸림
K-Means와의 차이
- K-Means : 각 점이 특정 클러스터에 하드 할당됨 → "너는 클러스터 2!"
- GMM : 각 점이 클러스터에 소프트 할당됨 → "너는 클러스터 1일 확률 0.7, 클러스터 2일 확률 0.3"
→ 확률 기반 클러스터링이라 더 유연하고 현실적
EM 알고리즘 (Expectation–Maximization)
- 데이터에 관찰되지 않는 숨겨진 변수(Z) 가 있어서, 직접적으로 우도(likelihood)를 최대화하기 어려움
- 그래서 "관찰된 데이터(X)" + "잠재 변수(Z)" 를 모두 고려한 완전 데이터(complete data) likelihood 를 정의
- 직접 계산이 어렵기 때문에 E-step과 M-step 을 번갈아 수행하면서 점진적으로 수렴
- 가우스 혼합 모델의 매개변수를 학습하기 위해 EM(Expectation-Maximization) 알고리즘을 사용
- 초기화
평균, 분산, 가중치를 적당히 설정 (예: K-평균 결과 활용) - E-step (Expectation)
현재 파라미터로 각 데이터가 클러스터 kk에 속할 사후확률(responsibility)을 계산 - M-step (Maximization)
이 사후확률을 기반으로 를 업데이트. - 수렴할 때까지 반복.
- 잠재 변수(Latent Variable)가 있는 확률 모델에서 최대우도추정을 구하는 방법
- 기대값에서는 현재 모수로 정의된 잠재 변수의 확률 분포에서 다음 단계 모수에 대한 로그 우도에 대한 기대값을 계산
- GMM의 잠재 변수에는 혼합 모델의 가우시안 분포들 중에서
각 관측값들이 어느 분포에서 생성된 것인지를 나타내는 변수가 존재
장점
- K-평균보다 유연 (공분산을 통해 타원형 클러스터 가능).
- 클러스터에 속할 확률을 제공 → 불확실성 평가 가능.
- 데이터의 잠재적 분포를 잘 설명할 수 있음.
- 밀도가 낮은 지역을 이상치로 탐지
단점
- 클러스터 수 KK를 미리 정해야 함.
- 초기값에 따라 결과가 달라질 수 있음.
- 고차원 데이터에서는 공분산 행렬 추정이 어려워질 수 있음.
이너셔
- 군집이 얼마나 잘 뭉쳐 있는지를 나타내는 척도 (kmeans.inertia_, -kmeans.score(X))
- 각 데이터 포인트와 자신이 속한 클러스터 중심 간의 거리 제곱을 모두 합한 값
- 작을수록 좋은 값이지만, 일반적으로 K가 증가하면 이너셔가 작아진다.

실루엣 계수
- (-1) ~ (+1), +1에 가까울수록 좋은 지표, -1에 가까우면 잘못된 클러스터에 할당

from sklearn.metrics import silhouette_samples, silhouette_score
import numpy as np
# 데이터 정의
X = np.array([
[1, 0],
[1, 1],
[3, 3],
[3, 2]
])
# 클러스터 레이블 정의
# (0,0)과 (0,1)은 클러스터 0, (3,4)와 (5,12)는 클러스터 1
labels = np.array([0, 0, 1, 1])
# 각 샘플의 실루엣 계수 계산
silhouette_vals = silhouette_samples(X, labels, metric='manhattan')
# (0,0)의 실루엣 계수는 인덱스 0
silhouette_vals # array([0.77777778, 0.71428571, 0.77777778, 0.71428571])
# (0.746031746031746, 0.746031746031746)
silhouette_score(X, labels, metric='manhattan'), silhouette_vals.mean()'개발 > Python' 카테고리의 다른 글
| 병합적 군집분석 계산 방법 비교 (linkage) (0) | 2025.09.08 |
|---|---|
| XGBoost Hyper Parameters and Attributes (0) | 2025.09.08 |
| MAE / MAPE / MSE / RMSE / MSLE / R2 (0) | 2025.09.08 |
| Threshold 조정에 따른 Precision과 Recall 결과 (0) | 2025.09.08 |
| 다항회귀모형 (PolynomialFeatures) (1) | 2025.08.21 |


댓글