MAE (Mean Absolute Error, 평균 절대 오차)
- 예측값과 실제값의 절대적 차이의 평균

특징
- 단순하고 직관적 (평균적으로 얼마나 벗어났는지)
- MSE 대비 이상치에 덜 민감
- 단위가 원래 데이터와 같음
전략
- 전반적으로 오차를 줄이는 모델 사용
- Median과 비슷한 성질 → L1 기반 모델(라쏘 회귀 등)과 잘 맞음
MAPE (Mean Absolute Percentage Error, 평균 절대 백분율 오차)
- 오차를 실제값에 대한 비율(%)로 환산한 값

특징
- 해석이 쉽다 : "평균적으로 몇 % 틀렸다"
- 실제값이 0 근처면 불안정 (0으로 나눔 문제)
- 값이 작은 샘플에 매우 민감
전략
- 실제값이 작은 데이터를 제거/보정 (0에 가깝지 않도록 전처리)
- 로그 변환을 통해 비율 오차 안정화
- 상대적 오차를 줄이는 방향으로 모델 학습 (log-loss 최적화)
MSE (Mean Squared Error, 평균 제곱 오차)
- 오차 제곱의 평균

특징
- 큰 오차(이상치)에 매우 민감
- 미분이 가능해서 경사하강법에 적합
- 단위가 원래 데이터의 제곱
전략
- 모델이 이상치에 과적합되지 않도록 Robust 모델 적용
- 정규화 / 스케일링을 통해 안정화
RMSE (Root Mean Squared Error, 평균 제곱근 오차)
- MSE의 제곱근

특징
- MSE와 달리 단위가 원래 데이터와 같음 → 해석이 쉽다
- 여전히 이상치에 민감
- MSE보다 직관적인 오차 척도
전략
- 이상치 처리 (클리핑, 로그 변환)
- 모델 정규화
- Gradient Boosting, Feature Scaling
MSLE (Mean Squared Logarithmic Error, 평균 제곱 로그 오차)
- 실제값과 예측값을 로그 변환한 뒤 제곱 평균

특징
- 상대적 오차를 줄여줌 (비율 차이를 강조)
- 큰 값보다는 작은 값 예측 정확도에 더 민감
- 0 또는 음수값 입력 불가
- 과소예측(under-prediction)에 관대, 과대예측에는 민감
전략
- 로그 스케일에서 잘 맞도록 모델 설계
- 큰 값보다 작은 값을 잘 예측하도록 튜닝
R² (Coefficient of Determination, 결정계수)
- 모델이 전체 변동을 얼마나 설명하는가
- 분자 : 예측 오차(잔차 제곱합, RSS)
- 분모 : 전체 변동(총제곱합, TSS)
- 독립변수가 1개라면 표본상관계수의 제곱과 같다.
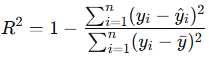
특징
- 1에 가까울수록 성능 좋음
- 0이면 단순 평균으로 예측한 것과 동일
- 음수가 나올 수도 있음 (평균보다 못한 모델)
전략
- 더 많은 특징 사용 (단, 과적합 주의)
- 비선형 관계 반영 (다항식 회귀, 트리 모델)
- 데이터 전처리 (정규화, 이상치 제거 등)
- 불필요한 피처 제거 + 중요한 피처 강화
- 데이터 스케일링, 차원 축소로 잡음 제거
Adjusted R² (수정된 결정계수)
- 결정계수는 특징 개수를 늘리면 증가하는 경향 → 쓸모없는 피처를 추가하면 성능이 감소해야 함.
- 결정계수에 패널티를 추가
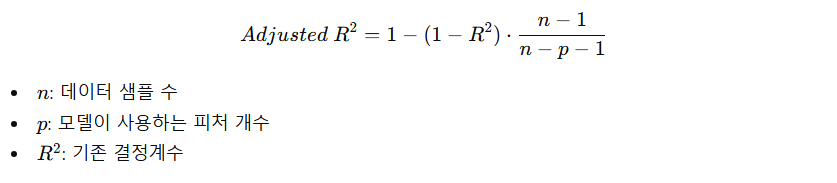
특징
- 특징 수 증가에 패널티 부여 → 쓸데없이 피처가 많아도 점수가 올라가지 않음
- 모델의 진짜 설명력 평가 → 단순 R²보다 모델 품질을 더 정확하게 나타냄
- 다중 회귀 모델에 유리 → 피처가 많은 고차원 데이터에서 특히 유용
- R²에 비해 비교 가능한 척도→ 서로 다른 피처 수의 모델 비교 가능
import numpy as np
from sklearn.metrics import (
mean_absolute_error,
mean_absolute_percentage_error,
mean_squared_error,
mean_squared_log_error,
r2_score
)
# ===== 예시 데이터 =====
y_true = np.array([10, 12, 15, 14, 18])
y_pred = np.array([9, 11, 16, 13, 17])
# ===== 지표 계산 =====
mae = mean_absolute_error(y_true, y_pred)
mape = mean_absolute_percentage_error(y_true, y_pred)
mse = mean_squared_error(y_true, y_pred)
rmse = np.sqrt(mse)
msle = mean_squared_log_error(y_true, y_pred)
r2 = r2_score(y_true, y_pred)
# ===== 결과 출력 =====
print(f"MAE : {mae:.4f}")
print(f"MAPE : {mape:.4f}")
print(f"MSE : {mse:.4f}")
print(f"RMSE : {rmse:.4f}")
print(f"MSLE : {msle:.6f}")
print(f"R2 : {r2:.4f}")
MAE : 1.0000
MAPE : 0.0700 (≈ 7%)
MSE : 1.0000
RMSE : 1.0000
MSLE : 0.0035
R2 : 0.9286'개발 > Python' 카테고리의 다른 글
| XGBoost Hyper Parameters and Attributes (0) | 2025.09.08 |
|---|---|
| 군집화 비교 (0) | 2025.09.08 |
| Threshold 조정에 따른 Precision과 Recall 결과 (0) | 2025.09.08 |
| 다항회귀모형 (PolynomialFeatures) (1) | 2025.08.21 |
| F-검정 통계량 문제 예시 (0) | 2025.08.21 |


댓글