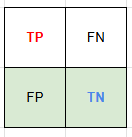
Confusion Matrix
| Positive (예측) | Negative (예측) | ||
| Positive (실제) | TP | FN | TP + FN = 실제 양성인 데이터 TP / (TP + FN) = Recall → TPR ---------------------------------- FN / (TP + FN) → 제 2종 오류 β |
| Negative (실제) | FP | TN | FP + TN = 실제 음성인 데이터 TN / (FP + TN) = Specificity ---------------------------------- FP / (FP + TN) = FPR → 제1종 오류 α |
| TP + FP = 양성으로 예측한 데이터 TP / (TP + FP) = Precision |
TP : 예측을 True / 실제도 True
FN : 예측을 False / 실제는 True
FP : 예측을 True / 실제는 False
TN : 예측을 False / 실제도 False
정밀도 - 예측이 Positive인 것 중 실제 Positive 비율

재현율 - 실제 Positive 중 올바르게 예측한 비율 (민감도, Sensitivity, TPR = 참 긍정률)

특이도 - 실제 Negative 중 올바르게 예측한 비율 (TNR)
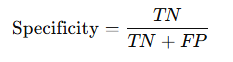

거짓 긍정률 - 실제 Negative 중 잘못 Positive로 예측한 비율 (FPR)
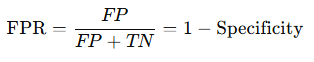

제1종 오류 확률 α : 유의수준, False Positive의 가능성
→ FP / (FP + TN)
→ FPR
→ 1 - 특이도
→ 실제 Negative를 Positive로 잘못 예측한 비율
제2종 오류 확률 β : False Negative 가능성
→ FN / (TP + FN)
→ FNR
→ 1 - 재현율
→ 실제 Positive를 Negative로 잘못 예측한 비율
1 - α : TN / (FP + TN) → 특이도
1 - β : 검정력 (Power) = 올바르게 H0를 기각할 확률 → TP / (TP + FN) → Recall (민감도)
제1종 오류 → 기존 주장이 무너지는 것이므로 더 큰 문제가 발생할 수 있음.
아래 데이터에 대해 로지스틱 회귀 결과를 확인해 보자.
import pandas as pd
import numpy as np
np.random.seed(1234)
n_samples = 300
X1 = np.random.normal(0, 1, n_samples)
X2 = np.random.normal(1, 2, n_samples)
# 로지스틱 회귀를 위한 이진 타겟 생성
y = (X1 + X2 + np.random.normal(0, 1, n_samples) > 1).astype(int)
df = pd.DataFrame({
"X1": X1,
"X2": X2,
"y": y
})
df
먼저 데이터를 분리한다.
from sklearn.model_selection import train_test_split
X = df[["X1", "X2"]]
y = df["y"]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=1234)
train으로 학습한 후, test 데이터에 대해 precision과 recall을 출력하면 다음과 같다.
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import precision_score, recall_score
model = LogisticRegression(solver='liblinear')
model.fit(X_train, y_train)
y_true = y_test
y_pred = model.predict(X_test)
precision_score(y_true, y_pred), recall_score(y_true, y_pred)
로지스틱 회귀는 predict_proba로 각 클래스 별 확률을 구할 수 있다.
위의 결과 predict는 확률이 50% 이상인 경우 1로 분류하고, 그렇지 않으면 0으로 분류한 결과다.
predict_proba에서 클래스 1일 확률만 얻은 후, 0.5보다 큰 값을 1이라고 한 것과 결과가 같은 것을 알 수 있다.
y_true = y_test
y_proba = model.predict_proba(X_test)[:, 1] # 클래스 1일 확률
y_pred = (y_proba > 0.5) * 1 # 50% 이상인 경우만 클래스 1로 판단
precision_score(y_true, y_pred), recall_score(y_true, y_pred)
기준이되는 확률(= threshold)을 50%보다 더 높이거나 낮추면 precision과 recall의 값이 조정된다.
precision이 중요한 상황
- False Positive(FP, 음성을 양성으로 잘못 분류)를 최소화해야 하는 상황
- 양성이라고 판정할 때, 정말 맞아야 하는 상황
- 법적/사법적 시스템: 범죄자 탐지, 부정 행위 적발 → 무고한 사람을 잘못 잡으면 큰 문제.
- 추천 시스템: 고객에게 상품 추천 → 쓸데없는 걸 추천하면 사용자 불만이 커짐.
- 광고 클릭 예측: 클릭 안 할 사람에게 광고를 계속 보여주면 비용 낭비.
- 채용 자동화 시스템: 적합하지 않은 사람을 합격시키는 것보다, 적합한 사람을 걸러내는 게 낫다고 판단될 때.
→ threshold를 높여서 더 확실한 경우에만 양성으로 판단한다.
recall이 중요한 상황
- False Negative(FN, 양성을 음성으로 잘못 분류)를 최소화해야 하는 상황
- 놓치면 안 되는 양성을 최대한 잡아내는 게 중요한 상황
- 의료 진단: 암, 전염병, 희귀병 같은 경우 → 환자를 놓치면 치명적임. (위양성은 추가 검사로 걸러낼 수 있음)
- 보안/위험 탐지: 폭발물 탐지, 스팸/피싱 탐지, 불법 거래 탐지 → 위험한 걸 놓치면 큰 피해.
- 재난 경보 시스템: 지진, 화재, 침수 등 위험 감지 → 놓치면 사람 목숨에 직결.
→ threshold를 낮춰서 양성일 가능성이 조금이라도 있으면 양성으로 판단한다.
→ 모두 Positive로 예측하면 FN이 0이 된다.
실제로 threshold를 0부터 0.9까지 바꿔보면 precision은 증가하고, recall은 감소하는 것을 알 수 있다.
for i in range(0, 10):
y_pred = (y_proba > (i / 10)) * 1
a = precision_score(y_true, y_pred)
b = recall_score(y_true, y_pred)
print(f"threshold : {i / 10}", f"precision : {a:.6f}", f"recall : {b:.6f}")
Threshold를 높이면 → FP 감소 → Precision ↑, TP도 줄어들 수 있음 → Recall ↓
Threshold를 낮추면 → TP ↑ → Recall ↑, FP도 늘어날 수 있음 → Precision ↓
위의 결과를 바탕으로 캐글에서 각 점수를 높이는 전략을 각각 세울 수 있다.
Precision (정밀도)
- 모델이 Positive라고 예측한 것 중 실제로 맞은 비율

- Threshold 높이기 : 0.7, 0.8 같은 임계값 적용 → 확실히 Positive일 때만 Positive로 분류
- Feature selection : 잡음(노이즈) 피처 제거 → FP 줄이기
- 이상치 제거 : 잘못된 라벨, 애매한 데이터 정리
- 앙상블에서 precision 높은 모델 가중치↑
- 데이터 불균형 문제 해결 : FP 줄이는 방향으로 학습 (예: hard negative mining)
Recall (재현율)
- 실제 정답(Positive) 중에서 모델이 맞게 찾아낸 비율
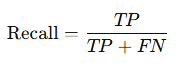
- Threshold 낮추기 : 0.5보다 작은 임계값을 적용하면 더 많은 데이터를 Positive로 분류 → FN 줄고 Recall ↑
- 클래스 가중치 조정 : class_weight="balanced" 같은 옵션 사용 → 소수 클래스 잘 잡음
- 데이터 증강/오버샘플링 : SMOTE 같은 기법으로 소수 클래스 샘플 늘리기
- 언더샘플링 : 다수 클래스 줄여서 소수 클래스 놓치지 않게 하기
- 앙상블에서 소수 클래스 민감 모델 가중치↑ : recall이 높은 모델을 여러 개 합쳐서 boost
F1 Score (조화평균)
- Precision과 Recall의 균형

- Threshold 튜닝 (Precision-Recall trade-off 최적점 찾기)
→ PR Curve에서 F1이 최대가 되는 지점 선택 - 데이터 증강 + Feature engineering : Recall과 Precision을 동시에 개선
- 앙상블 기법 (Voting/Stacking) : 서로 다른 모델의 장점을 결합
- Cross-validation 기반 hyperparameter tuning : overfitting 방지 + 균형 성능 유지
Macro F1 Score (클래스 불균형 고려)
- 각 클래스별 F1 Score를 계산한 후 평균낸 값 (클래스별 가중치 동일)

- 클래스 불균형 해소 : 소수 클래스 oversampling, 데이터 증강
- 클래스 가중치 부여 : class_weight 조정
- 다중 클래스 분류기 튜닝 : 각 클래스에서 고르게 성능 나오게 만들기
- One-vs-Rest 학습 : 각 클래스에 대해 개별적으로 최적화
- Threshold per class : 클래스별 decision threshold 조정
'개발 > Python' 카테고리의 다른 글
| 군집화 비교 (0) | 2025.09.08 |
|---|---|
| MAE / MAPE / MSE / RMSE / MSLE / R2 (0) | 2025.09.08 |
| 다항회귀모형 (PolynomialFeatures) (1) | 2025.08.21 |
| F-검정 통계량 문제 예시 (0) | 2025.08.21 |
| 포아송 분포 문제 예시 (0) | 2025.08.21 |

댓글