반응형
X, y의 관계가 비선형일 때, X의 거듭제곱 항을 추가해서 모델링을 할 수 있다.
아래 데이터에 대해 PolynomialFeatures를 이용하여 다항회귀모형을 만들어 보자.
import pandas as pd
df = pd.DataFrame({
'X1': [1, 2, 3, 4, 5],
'X2': [2, 3, 4, 5, 6],
'X3': [3, 4, 5, 6, 7],
'y': [10, 20, 30, 40, 50]
})
df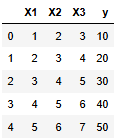
PolynomialFeatures에서 degree 옵션과 include_bias 옵션을 이용하면 다항식을 만들 수 있다.
get_feature_names를 이용하여 새로 만들어진 데이터를 쉽게 확인할 수 있다.
from sklearn.preprocessing import PolynomialFeatures
# 독립변수(X)와 종속변수(y) 분리
X = df[['X1', 'X2', 'X3']]
y = df['y']
# degree=2 다항 특성 변환
poly = PolynomialFeatures(degree=2, include_bias=False)
X_poly = poly.fit_transform(X)
# 변환된 데이터를 새로운 DataFrame으로 표시
df_poly = pd.DataFrame(X_poly, columns=poly.get_feature_names(['X1', 'X2', 'X3']))
df_poly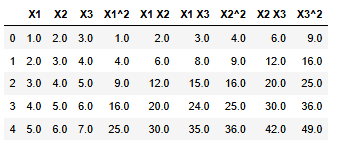
* 참고 : 이름에 공백을 제거하고 싶다면 str.replace를 사용
df_poly.columns.str.replace(" ", "_")
# Index(['X1', 'X2', 'X3', 'X1^2', 'X1_X2', 'X1_X3', 'X2^2', 'X2_X3', 'X3^2'], dtype='object')
interaction_only=True로 할 경우 교차항만 생성된다.
from sklearn.preprocessing import PolynomialFeatures
# 독립변수(X)와 종속변수(y) 분리
X = df[['X1', 'X2', 'X3']]
y = df['y']
# degree=2 다항 특성 변환
poly = PolynomialFeatures(degree=2, include_bias=False, interaction_only=True)
X_poly = poly.fit_transform(X)
# 변환된 데이터를 새로운 DataFrame으로 표시
df_poly = pd.DataFrame(X_poly, columns=poly.get_feature_names(['X1', 'X2', 'X3']))
df_poly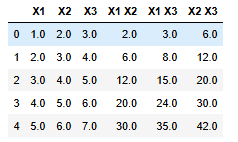
이후 선형회귀와 마찬가지로 모형을 만들면 된다.
from sklearn.linear_model import LinearRegression
model = LinearRegression()
model.fit(X_poly, y)
y_pred = model.predict(X_poly)
df_poly['y_actual'] = y
df_poly['y_predicted'] = y_pred
df_poly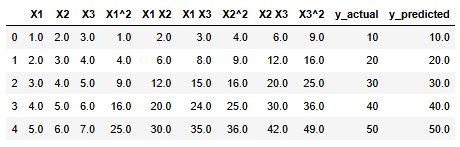
반응형
'개발 > Python' 카테고리의 다른 글
| MAE / MAPE / MSE / RMSE / MSLE / R2 (0) | 2025.09.08 |
|---|---|
| Threshold 조정에 따른 Precision과 Recall 결과 (0) | 2025.09.08 |
| F-검정 통계량 문제 예시 (0) | 2025.08.21 |
| 포아송 분포 문제 예시 (0) | 2025.08.21 |
| ROC 커브의 AUC 계산 (0) | 2025.08.19 |
댓글