정규성 검정
- Shapiro-Wilk Test : 통계량을 계산하여 정규성을 검정하는 기법, 데이터의 수가 많지 않을 때 사용
- Kolmogorov-Smirnov : 경험적 분포와 이론 분포의 최대 차이를 이용 (누적분포 비교)
- Lilliefors : K-S 검정의 변형, 정규분포의 모수를 데이터로 추정할 때 사용
- Anderson-Darling : K-S보다 꼬리 부분에 민감
- Jarque-Bera Test : 왜도와 첨도가 정규분포 (0, 3)와 같은지 비교, 샘플 수가 적을 때 검정력이 낮음.
- Cramer-von Mises
- Q-Q Plot : 분위수를 활용한 시각적 평가 (p-value 미제공)
- 정규화된 차이 비교
귀무가설 : 데이터는 정규분포를 따른다.
대립가설 : 데이터는 정규분포를 따르지 않는다.
Q-Q Plot
import numpy as np
import scipy.stats as stats
import matplotlib.pyplot as plt
def plot_all_distributions():
distributions = {
"Normal Distribution": np.random.normal(0, 1, 1000),
"Right-Skewed Distribution": stats.skewnorm.rvs(a=10, loc=0, scale=1, size=1000),
"Left-Skewed Distribution": stats.skewnorm.rvs(a=-10, loc=0, scale=1, size=1000),
"Exponential Distribution (Right-skewed)": np.random.exponential(scale=1, size=1000),
"Binomial Distribution": np.random.binomial(n=10, p=0.3, size=1000),
"Uniform Distribution": np.random.uniform(-2, 2, 1000)
}
fig, axes = plt.subplots(len(distributions), 2, figsize=(12, len(distributions) * 3))
for i, (title, data) in enumerate(distributions.items()):
# 히스토그램
axes[i, 0].hist(data, bins=30, color='skyblue', edgecolor='black')
axes[i, 0].set_title(f"{title} - Histogram")
# Q-Q plot
stats.probplot(data, dist="norm", plot=axes[i, 1])
axes[i, 1].set_title(f"{title} - Q-Q Plot")
plt.tight_layout()
plt.show()
plot_all_distributions()

정규화된 차이 비교
다음 데이터에서 변수별로 백분위수 (5, 10, ..., 95)를 구하고
변수의 평균과 표준 편차를 따르는 정규분포의 백분위수(5, 10, ..., 95)와 비교하라.
(대응되는 값의 차이의 제곱의 합의 평균을 구하라)
import pandas as pd
import numpy as np
np.random.seed(1234)
df = pd.DataFrame(
np.random.randn(100, 5),
columns=[f'X{i+1}' for i in range(5)]
)
# X1: 지수분포 (비대칭, 양수만)
df['X1'] = np.random.exponential(scale=1.0, size=100)
# X3: 균등분포 (-3 ~ 3 범위)
df['X3'] = np.random.uniform(-3, 3, size=100)
df
위에서 제시한대로 데이터의 백분위 수와 정규분포의 백분위 수(ppf)의 차이를 구하는 함수는 다음과 같이 구할 수 있다.
from scipy.stats import norm
def diff(srs):
a = []
b = []
mean = srs.mean()
std = srs.std()
n = norm(loc=mean, scale=std)
for p in range(5, 100, 5):
a.append(n.ppf(p / 100))
b.append(srs.quantile(p / 100))
return ((np.array(a) - np.array(b)) ** 2).mean()
변수별로 결과를 출력하면 다음과 같다.
X1과 X3가 정규분포가 아니기 때문에 값이 상대적으로 큰 것을 알 수 있다.
for col in df.columns.tolist():
print(diff(df[col]))
shapiro 검정을 해봐도 X1과 X3는 정규분포를 따르지 않는다는 것을 알 수 있다.
from scipy.stats import shapiro
alpha = 0.05
for col in df.columns.tolist():
stat, pval = shapiro(df[col])
print(stat, pval)
if pval > alpha:
print("귀무가설 채택 → 정규분포를 따른다")
else:
print("귀무가설 기각 → 정규분포를 따르지 않는다")
참고
PDF (Probability Density Function)
- 정규 분포의 높이를 보여주는 함수
- 분포의 모양(대칭성, 꼬리, 첨도)을 알고 싶을 때 사용

즉, (0, 1)을 따르는 정규분포에 f(x) = pdf(x)가 된다.
norm.pdf(0), 1 / np.sqrt(2 * np.pi) * np.exp(0)

정규분포 확률 밀도 함수(PDF) 계산
from scipy.stats import norm
import numpy as np
import matplotlib.pyplot as plt
# 평균 0, 표준편차 1 정규분포
mu = 0
sigma = 1
x = np.linspace(-4, 4, 100)
pdf = norm.pdf(x, loc=mu, scale=sigma)
plt.plot(x, pdf, label='Normal PDF')
plt.title('Standard Normal Distribution')
plt.xlabel('x')
plt.ylabel('Probability Density')
plt.legend()
plt.show()
CDF (Cumulative Distribution Function)
- 누적확률 = F(x) = P(X<=x)
- p-value 계산시 사용
예를 들어 cdf(0)은 정규분포의 절반이므로 0.5가 나온다.
norm.cdf(0) # 0.5
평균 100, 표준편차 15일 때 X > 130일 확률
p = 1 - norm.cdf(130, loc=100, scale=15)
print("P(X > 130) =", p)PPF (Percent Point Function) = Quantile = CDF의 역함수
- 분위수 기반 기준선을 구할 때 사용
- 확률 → 값으로 변경 시 사용
cdf의 역함수이므로 ppf(0.5)는 0이 나오게 된다. (cdf(0) = 0.5)
norm.ppf(0.5) # 0.0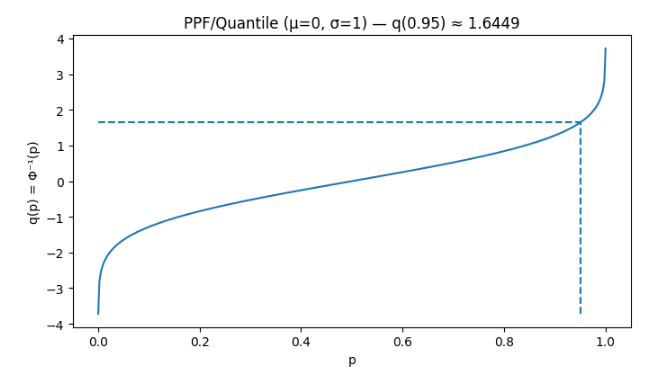
상위 2.5% 지점 (신뢰구간 계산 시)
q = norm.ppf(0.975, loc=0, scale=1)
print("97.5% 분위수 =", q) # 1.959963984540054랜덤 샘플 생성
samples = norm.rvs(loc=0, scale=1, size=10)
print("Random samples:", samples)
# Random samples: [ 2.1221562 1.03246526 -1.51936997 -0.48423407 1.26691115 -0.70766947
# 0.44381943 0.77463405 -0.92693047 -0.05952536]'개발 > Python' 카테고리의 다른 글
| 일원분산분석 비교 (f_oneway vs anova_lm) (2) | 2025.08.15 |
|---|---|
| 데이터 범주화, 구간화 (1) | 2025.08.15 |
| SVM Hyper Parameters and Attributes (1) | 2025.08.14 |
| 선형회귀모형의 변수 선택 (후진제거법, 전진선택법) (1) | 2025.08.14 |
| 병합적 군집분석 결과를 다른 데이터 샘플에 적용하기 (3) | 2025.08.13 |




댓글