가정
독립성 - 관측값은 서로 독립이어야 한다.
정규성 - 정규분포를 따른다고 가정 (Shapiro-Wilk, 콜모고로프-스미르노프 검정)
등분산성 - 모든 그룹의 분산이 동일하다고 가정 (Bartlett, 레빈 검정, 브라운-포사이트 검정)
scipy.stats.f_oneway
- 단순히 그룹 간 평균 차이를 검증
- 그룹별 데이터 배열을 입력
statsmodels.stats.anova.anova_lm
- 선형모델(OLS) 기반의 ANOVA 테이블 생성
- ols()로 만든 모델 객체를 입력
일원분산분석의 가정
독립성 : 각 집단 내 표본들은 서로 독립적이어야 한다. 즉, 한 표본의 값이 다른 표본의 값에 영향을 미치지 않아야 한다.
정규성 : 각 집단의 데이터가 정규분포를 따라야 한다. 특히, 각 집단 내 잔차(residual)가 정규성을 만족하는지 확인한다.
등분산성 : 모든 집단의 분산이 서로 동일하거나 거의 비슷해야 한다. 즉, 각 집단의 데이터가 같은 분산을 가져야 한다.
귀무가설 : 모든 그룹의 모평균이 같다.
대립가설 : 적어도 하나의 그룹의 평균이 다르다.
정규성이나 등분산성이 안 맞는 경우엔 Kruskal-Wallis 등의 비모수 검정 사용
귀무가설 : 모든 그룹의 중앙값이 같다.
대립가설 : 적어도 하나의 그룹의 중앙값은 다르다.
from scipy.stats import kruskal
...
statistic, p_value = kruskal(group1, group2, group3)"과목"에 따른 "점수" 변수의 평균에 유의미한 차이가 존재하는지 검정하라.
import pandas as pd
import numpy as np
np.random.seed(1234)
num_students = 10
data = {
'국어': np.random.randint(50, 101, size=num_students),
'영어': np.random.randint(50, 101, size=num_students),
'수학': np.random.randint(50, 101, size=num_students)
}
df = pd.DataFrame(data)
df
과목에 따라 점수가 나뉘어져 있으므로 f_oneway로 검증할 수 있다.
from scipy.stats import f_oneway
f_oneway(df['국어'], df['영어'], df['수학'])
anova_lm을 사용하기 위해서는 입력데이터가 데이터프레임 + 모델 형태가 되어야 한다.
melt()를 이용해 다음과 같이 데이터를 수정할 수 있다.
df_long = pd.melt(df, value_vars=['국어', '영어', '수학'], var_name='과목', value_name='점수')
df_long = df_long.reset_index(drop=True)
df_long
ols로 모델을 만든 후 anova_lm의 결과를 출력하면 분산분석표를 얻을 수 있다.
from statsmodels.formula.api import ols
from statsmodels.stats.anova import anova_lm
# ols 모델 생성: (종속변수 ~ 독립변수) -> 점수 ~ C(과목)
model = ols('점수 ~ C(과목)', data=df_long).fit()
result = anova_lm(model)
result
# C(group)는 그룹 간 차이에 대한 효과
# sum_sq : 제곱합
# mean_sq : 평균 제곱합, sum_sq / df
# df : 자유도
# F : F 통계량, 그룹 간 변동이 그룹 내 변동보다 얼마나 큰지 비교 (F가 크면 통계적으로 유의)
# PR(>F): p-value (0.05보다 작으면 그룹 간 평균 차이가 유의함)
f_oneway의 stat과 pvalue와 같은 값임을 알 수 있다.
result['F'][0], result['PR(>F)'][0]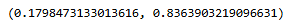
참고
일원분산분석 검정에서, 표본의 평균이 같으면 처리제곱합이 0이다.

import numpy as np
# 그룹별 데이터 (평균이 모두 같음)
group1 = np.array([4, 5, 6])
group2 = np.array([5, 5, 5])
group3 = np.array([2, 5, 8])
# 각 그룹 평균
mean1 = np.mean(group1)
mean2 = np.mean(group2)
mean3 = np.mean(group3)
# 전체 데이터 합치기
all_data = np.concatenate([group1, group2, group3])
overall_mean = np.mean(all_data)
# 그룹별 표본 수
n1 = len(group1)
n2 = len(group2)
n3 = len(group3)
# 처리 제곱합 계산 (SS_between)
SS_between = n1 * (mean1 - overall_mean)**2 + n2 * (mean2 - overall_mean)**2 + n3 * (mean3 - overall_mean)**2
print(f"그룹1 평균: {mean1}, 그룹2 평균: {mean2}, 그룹3 평균: {mean3}") # 5.0
print(f"전체 평균: {overall_mean}") # 5.0
print(f"처리 제곱합 (SS_between): {SS_between}") # 0.0anova_lm typ
Type I (typ=1) : 순차형 ANOVA
- 변수를 모델에 입력한 순서대로 기여도를 평가.
- ex. model = ols("y ~ X1 + X2 + X3").fit() 이라면,
- X1 → X1이 제일 먼저 기여도 평가
- X2 → X1이 들어간 모델에 추가되어 기여도 평가
- X3 → (X1+X2) 이후 기여도 평가
- 변수 순서 변경 시 결과가 달라짐
- 실험 디자인에서 잘 사용되지 않음
Type II (typ=2) : 부분형 / 계층형 ANOVA
- 한 변수를 평가할 때, 다른 주효과(main effect)들은 모두 고려.
- 하지만 상호작용(interaction)을 포함하면 부정확할 수 있음
- 상호작용이 없는 모델(예: 다중회귀, 요인 독립)에서 사용
- 상호작용이 있을 경우 적절하지 않음
Type III (typ=3) : 완전형 / 부분형 ANOVA
- 각 변수를 평가할 때, 다른 모든 주효과 + 상호작용까지 고려.
- 실험 계획법(실험데이터)에서 가장 많이 사용.
- 상호작용 포함 모델에서 권장
- 변수 순서와 무관
- 절편(intercept) 반드시 필요
import numpy as np
import pandas as pd
import statsmodels.api as sm
from statsmodels.formula.api import ols
from statsmodels.stats.anova import anova_lm
# --------------------
# 1) 데이터 생성
# --------------------
np.random.seed(0)
n = 40
X1 = np.random.choice(['A', 'B'], size=n) # 범주형 변수 1
X2 = np.random.choice(['C', 'D'], size=n) # 범주형 변수 2
# 실제 데이터에 상호작용을 넣자
Y = (
3 + # 절편
(X1 == 'B') * 2 + # X1 효과
(X2 == 'D') * 4 + # X2 효과
( (X1 == 'B') & (X2 == 'D') ) * 5 + # 상호작용 효과
np.random.normal(0, 1, size=n) # 잡음
)
df = pd.DataFrame({'Y': Y, 'X1': X1, 'X2': X2})
# --------------------
# 2) OLS 모델 적합
# --------------------
model = ols("Y ~ C(X1) * C(X2)", data=df).fit()
# --------------------
# 3) ANOVA Type I / II / III 비교
# --------------------
print("\n=== Type I (순차적) ===")
print(anova_lm(model, typ=1))
print("\n=== Type II (상호작용 고려하지 않음) ===")
print(anova_lm(model, typ=2))
print("\n=== Type III (상호작용 포함 완전형 분석) ===")
print(anova_lm(model, typ=3))
'개발 > Python' 카테고리의 다른 글
| statsmodels ols 결과 출력하기 (1) | 2025.08.15 |
|---|---|
| 결정 트리 (분기 전후의 지니 불순도 감소량) (1) | 2025.08.15 |
| 데이터 범주화, 구간화 (1) | 2025.08.15 |
| 정규성 검정 (2) | 2025.08.15 |
| SVM Hyper Parameters and Attributes (1) | 2025.08.14 |




댓글