변수선택법
필터 방법 (Filter Methods)
- 데이터의 통계적 특성을 이용해 변수의 중요도를 미리 평가한 뒤 선택하는 방법.
- 변수 간의 상호작용을 고려하기 어려움.
- 상관계수 (Correlation) : 종속 변수와의 상관관계가 큰 변수 선택
- 카이제곱 검정 (Chi-square test) : 범주형 독립변수와 범주형 종속변수의 독립성 확인
- ANOVA / F-test : 범주형 독립변수와 연속형 종속변수의 관련성 확인
- 정보 이득 (Information Gain), 엔트로피, Gini Index
- 분산 기준 (Variance Threshold) : 분산이 작은 변수 제거
래퍼 방법 (Wrapper Methods)
- 실제로 모델을 학습시키고 성능 기준으로 변수를 선택하는 방법.
- 필터 방법보다 연산량이 많음.
- 변수 간의 상호작용을 고려
- 전진 선택법 (Forward Selection)
- 아무 변수도 없는 상태에서 시작해서, 성능이 개선되지 않을 때까지 변수를 선택
- 후진 제거법 (Backward Elimination)
- 많은 독립변수(feature) 중에서 불필요한 변수를 제거해서 모델을 단순화하는 방법
- 모든 변수를 포함해서 학습하고, 특정 성능 지표(AIC, BIC 등)를 기준으로 가장 기여도가 낮은 변수를 제거
- 단계적 선택법 (Stepwise Selection) : 전진 + 후진을 혼합 (변수 추가/제거 반복)
- Best Subset Selection : 가능한 모든 변수 조합 비교 (계산량 많음)
임베디드 방법 (Embedded Methods)
- 모델 학습 과정에서 변수 선택이 동시에 이루어지는 방법.
- Lasso 회귀 (L1 정규화) : 중요하지 않은 변수 계수를 0으로 만듦 → 변수 선택 효과
- Ridge 회귀 (L2 정규화) : 변수 선택보다는 계수 축소(regularization)에 유용
- Elastic Net : L1 + L2 혼합 → 변수 선택과 안정성 동시에 확보
- 의사결정나무 기반 중요도 (Random Forest, XGBoost feature importance)
차원 축소 기반 방법
- 직접적으로 "변수 선택"은 아니지만, 변수 수를 줄이는 데 활용됨. (변수 축소 효과)
- PCA (주성분 분석) : 기존 변수들을 선형 결합해 새로운 변수 생성
- LDA (선형판별분석) : 클래스 분리를 잘하는 축으로 차원 축소
- t-SNE, UMAP : 비선형 차원 축소
후진제거법
다음과 같이 15개의 독립변수에서 절편을 제외하여 학습하면서 불필요한 변수를 제거해보자. (대상 지표 : AIC)
import pandas as pd
import numpy as np
np.random.seed(1234)
# 100행 × 15개 독립변수 생성
X = pd.DataFrame(
np.random.randn(100, 15),
columns=[f'X{i+1}' for i in range(15)]
)
# 3의 배수 컬럼 선택
cols_3_multiple = [col for col in X.columns if int(col[1:]) % 3 == 0]
# 랜덤 가중치 생성
weights = np.random.uniform(1, 5, size=len(cols_3_multiple))
# 선형 결합으로 y 생성
y = X[cols_3_multiple].dot(weights) + np.random.randn(100) * 0.5 # 약간의 노이즈 추가
# DataFrame 결합
df = X.copy()
df['y'] = y
df
독립변수를 cols에 저장하고 join을 이용해 수식을 만든다.
cols = df.columns.tolist()
cols.remove('y')
X = " + ".join(cols)
X
statsmodels의 ols를 이용해서 선형모델을 만들 수 있다.
절편을 제외하기 위해 수식에 " + 0 "을 추가하였다.
from statsmodels.formula.api import ols
# 절편 제외 + 0
model = ols(f"y ~ {X} + 0", df).fit()
model.aic
이제 후진제거법을 실행하면 된다.
후진제거법은 변수를 제거하는 방법이기 때문에 많아야 전체 독립변수의 개수만큼만 실행할 수 있다.
변수를 하나씩 제거하면서 aic를 계산하고, 이때 가장 작은 aic와 모든 변수로 학습한 aic를 비교한다.
더 작은 aic가 존재한다면 그 값을 갱신해나가면서 aic가 더 이상 작아지지 않을 때 까지 반복하면 된다.
아래 코드를 실행하고 last_col을 출력하면 후진제거법에 의해 남아있는 변수만 출력된다.
step = len(cols) # 후진제거법 최대 횟수 = 전체 독립변수의 개수
target = cols.copy() # 대상 독립변수
start_aic = model.aic # 기준이 되는 aic
for _ in range(step):
list_aic = []
for col in target:
selected = [i for i in target if i is not col] # 하나의 변수를 제외하고
X = " + ".join(selected)
model = ols(f"y ~ {X} + 0", df).fit() # 다시 모델을 만들어서
list_aic.append(model.aic) # aic를 계산
min_aic = min(list_aic) # aic 중 가장 작은 값
min_col = target[np.array(list_aic).argmin()] # aic를 가장 작게 만든 독립변수
last_col = target.copy() # 최종 target 변수를 확인하기 위한 변수
if start_aic <= min_aic : break # 현재까지 최소의 aic와 비교
print(start_aic, min_aic, " deleted :", min_col)
target.remove(min_col) # 대상 독립변수에서 삭제
start_aic = min_aic # aic 갱신
last_col
전진선택법
위의 데이터에 대해 전진선택법으로 colB까지 변수를 선택했다고 가정하자.
colA에서 aic를 기준으로 4개의 변수를 더 선택하라.
colA = ['X1', 'X2', 'X3', 'X4', 'X5', 'X6', 'X7']
colB = ['X8', 'X9', 'X10', 'X11', 'X12', 'X13', 'X14', 'X15']대상 변수에서 하나씩 검토하는 것은 후진제거법과 같다.
다만 전진선택법은 aic를 작게 만드는 변수를 추가하도록 코드를 수정하였다.
from statsmodels.formula.api import ols
for _ in range(4): # 변수 선택 4번
aic = []
for col in colA: # colA에서
cols = [col] + colB # colB에 변수 하나를 추가
X = " + ".join(cols)
model = ols(f"y ~ {X} + 0", df).fit() # 모델 학습
aic.append(model.aic)
selected = colA[np.array(aic).argmin()] # aic를 가장 작게 만드는 변수 선택
colA.remove(selected) # colA에서 제거
colB = [selected] + colB # colB에 추가
print(colB)
AIC vs BIC
- 값이 작을수록 좋은 모델로 판단
- 최대우도값을 이용해서 점수 계산
- BIC는 데이터의 개수 (n)에 의한 패널티 증가가 존재
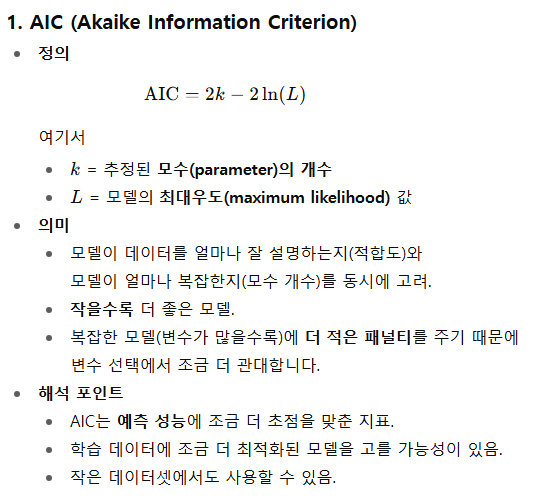


AIC
- 정확도와 간명성 사이의 상충을 조절하려는 방법, 많은 독립 변수를 갖는 모형에 패널티
- 데이터에 더 잘 맞추는 모델을 선호, 모델 예측 성능 중요 (조금 더 유연하게 변수 포함, 보편화)
BIC
- 불필요하게 복잡하지 않은 모델을 선호, 모델 분석 중요 (변수를 더 과감히 줄임)
- AIC보다 더 강한 패널티를 부여, 독립변수의 개수 x log(관측치의 개수)의 패널티를 부여
* 모형선택의 일치성
- 통계 모델을 선택하는 절차가 샘플 수가 무한히 커질 때(true 모델을) 정확히 찾아낼 확률이 1로 수렴하는 성질
- AIC : 작은 샘플에서는 좋은 성능, 하지만 일치성은 보장되지 않음. → 과적합 경향
- BIC : 일치성 → 표본 수 ↑ 진짜 모형 선택 확률 → BIC는 데이터가 많아질수록 진짜 모형을 선택할 확률이 1로 수렴
그 외 RIC, CIC, DIC가 존재
RIC (Risk Inflation Criterion)
- 회귀모형에서 불필요한 변수 포함 시 위험(risk) 증가를 조정
- 변수 선택 시, 포함되는 변수 수가 늘어날수록 예측오차가 증가하는 것을 벌점(penalty)으로 반영
- 큰 표본에서는 일치성(consistency)을 갖도록 설계 가능
- 주로 고차원 회귀(high-dimensional regression)에서 변수 선택에 사용
- AIC보다 변수 선택에 더 보수적
- 과적합(overfitting) 방지에 도움
CIC (Criterion for Information Complexity)
- 모델의 예측 정확도와 복잡도를 동시에 고려
- 모델의 자유도(free parameters)와 정보 손실을 동시에 고려
- AIC처럼 예측 오차를 최소화하면서, 모델의 복잡도를 반영하여 과적합 방지
- 통계 모델뿐 아니라, 정보이론 기반 모형 선택에 적합
- 상대적으로 복잡한 모형 선택 기준
- 샘플이 작아도 어느 정도 안정적
DIC (Deviance Information Criterion)
- 베이지안 모델 선택(Bayesian Model Selection)
- DIC = 평균 deviance + penalty for effective number of parameters
- deviance = -2 * log-likelihood
- 모형 적합도 측정 → deviance 평균
- 모형 복잡도 측정 → effective number of parameters
- MCMC 기반 Bayesian 모델에서 주로 사용
- 값이 작을수록 좋은 모델
- 일반적인 AIC/BIC와 달리 Bayesian posterior 분포를 사용
- 복잡한 hierarchical 모델에도 적용 가능
'개발 > Python' 카테고리의 다른 글
| 정규성 검정 (2) | 2025.08.15 |
|---|---|
| SVM Hyper Parameters and Attributes (1) | 2025.08.14 |
| 병합적 군집분석 결과를 다른 데이터 샘플에 적용하기 (3) | 2025.08.13 |
| Pandas 전처리 - 이상치 탐지 (4) | 2025.08.12 |
| 그룹 별 변수들의 차이 비교 (일원분산분석 vs Kruskal-Wallis 검정) (4) | 2025.08.10 |




댓글