과소적합
- 모델이 데이터의 패턴을 충분히 배우지 못한 상태
- 학습 데이터와 테스트 데이터 모두에서 성능이 낮음
- 학습 데이터가 불충분, 중요한 특성을 사용하지 않은 상태
과대적합
- 학습 데이터의 성능이 높고, 평가 데이터의 성능은 낮은 상태 (노이즈까지 학습한 상태)
- 학습 데이터의 패턴을 지나치게 학습하여 편향이 낮아진 상태
- 데이터의 작은 변화에도 민감하게 반응 → 분산이 높은 상태
선형 회귀
→ Ridge / Lasso 규제 추가
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression, Ridge, Lasso
from sklearn.preprocessing import PolynomialFeatures
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
# 1. 데이터 생성
np.random.seed(0)
X = np.linspace(0, 1, 50)[:, np.newaxis] # 0~1 사이 50개
y = np.sin(2 * np.pi * X).ravel() + np.random.randn(50) * 0.3 # 노이즈 포함
# 2. 다항특성 생성 (과대적합 유발)
poly = PolynomialFeatures(degree=15) # 15차 다항식 -> 과대적합
X_poly = poly.fit_transform(X)
# 3. 학습/테스트 데이터 분리
X_train, X_test, y_train, y_test = train_test_split(X_poly, y, test_size=0.2, random_state=42)
# 4. 모델 학습
# 4-1. Linear Regression (과대적합)
lr = LinearRegression()
lr.fit(X_train, y_train)
y_train_pred = lr.predict(X_train)
y_test_pred = lr.predict(X_test)
# 4-2. Ridge Regression
ridge = Ridge(alpha=1.0)
ridge.fit(X_train, y_train)
y_ridge_pred = ridge.predict(X_test)
# 4-3. Lasso Regression
lasso = Lasso(alpha=0.01, max_iter=10000)
lasso.fit(X_train, y_train)
y_lasso_pred = lasso.predict(X_test)
# 5. 결과 확인
print("Linear Regression MSE (train/test):", mean_squared_error(y_train, y_train_pred), "/", mean_squared_error(y_test, y_test_pred))
print("Ridge MSE (test):", mean_squared_error(y_test, y_ridge_pred))
print("Lasso MSE (test):", mean_squared_error(y_test, y_lasso_pred))
# 6. 시각화
plt.figure(figsize=(12,6))
plt.scatter(X, y, color='black', label='data')
plt.plot(X, lr.predict(X_poly), label='Linear Regression', color='red')
plt.plot(X, ridge.predict(X_poly), label='Ridge', color='blue')
plt.plot(X, lasso.predict(X_poly), label='Lasso', color='green')
plt.legend()
plt.show()
Ridge / Lasso
- λ (또는 α) ↑ (크게)
- 규제 강도를 높이면 가중치가 작아져 모델 단순화
import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import Ridge, Lasso
from sklearn.model_selection import train_test_split
# 1. 데이터 생성
np.random.seed(0)
X = np.linspace(0, 1, 30)[:, np.newaxis]
y = np.sin(2 * np.pi * X).ravel() + np.random.randn(30) * 0.3
# 2. 다항특성 생성 (10차 다항식)
poly = PolynomialFeatures(degree=10)
X_poly = poly.fit_transform(X)
# 3. 학습/테스트 분리
X_train, X_test, y_train, y_test = train_test_split(X_poly, y, test_size=0.3, random_state=42)
# 4. α 값 리스트
alphas = [10, 1, 0.1, 0.01, 0.0001]
# 5. 시각화
plt.figure(figsize=(14,6))
for i, alpha in enumerate(alphas):
# Ridge
ridge = Ridge(alpha=alpha)
ridge.fit(X_train, y_train)
y_ridge_pred = ridge.predict(X_poly)
# Lasso
lasso = Lasso(alpha=alpha, max_iter=10000)
lasso.fit(X_train, y_train)
y_lasso_pred = lasso.predict(X_poly)
# Plot Ridge
plt.subplot(2, len(alphas), i+1)
plt.scatter(X, y, color='black')
plt.plot(X, y_ridge_pred, color='blue')
plt.title(f'Ridge α={alpha}')
# Plot Lasso
plt.subplot(2, len(alphas), i+1+len(alphas))
plt.scatter(X, y, color='black')
plt.plot(X, y_lasso_pred, color='green')
plt.title(f'Lasso α={alpha}')
plt.tight_layout()
plt.show()

Logistic Regression
- C ↓ : 규제 강도의 역수, 작아지면 규제가 강해지고 → 과대적합 완화
- 규제 L1, L2 추가
SVM
- C (규제 강도), gamma (커널 영향 범위) 를 감소
SVC
import numpy as np
import matplotlib.pyplot as plt
from sklearn.svm import SVC
from sklearn.datasets import make_moons
# 2차원 분류 데이터 생성
X, y = make_moons(n_samples=200, noise=0.2, random_state=42)
# C와 gamma 후보
C_values = [0.1, 1, 10]
gamma_values = [0.1, 1, 10]
plt.figure(figsize=(12, 12))
# 3x3 그리드로 그리기
for i, C in enumerate(C_values):
for j, gamma in enumerate(gamma_values):
svc = SVC(C=C, gamma=gamma)
svc.fit(X, y)
# 결정 경계 그리기
x_min, x_max = X[:, 0].min() - 0.5, X[:, 0].max() + 0.5
y_min, y_max = X[:, 1].min() - 0.5, X[:, 1].max() + 0.5
xx, yy = np.meshgrid(np.linspace(x_min, x_max, 200),
np.linspace(y_min, y_max, 200))
Z = svc.predict(np.c_[xx.ravel(), yy.ravel()]).reshape(xx.shape)
plt.subplot(3, 3, i*3 + j + 1)
plt.contourf(xx, yy, Z, alpha=0.3, cmap=plt.cm.coolwarm)
plt.scatter(X[:, 0], X[:, 1], c=y, s=30, cmap=plt.cm.coolwarm, edgecolors='k')
plt.title(f"C={C}, gamma={gamma}")
plt.xlim(xx.min(), xx.max())
plt.ylim(yy.min(), yy.max())
plt.tight_layout()
plt.show()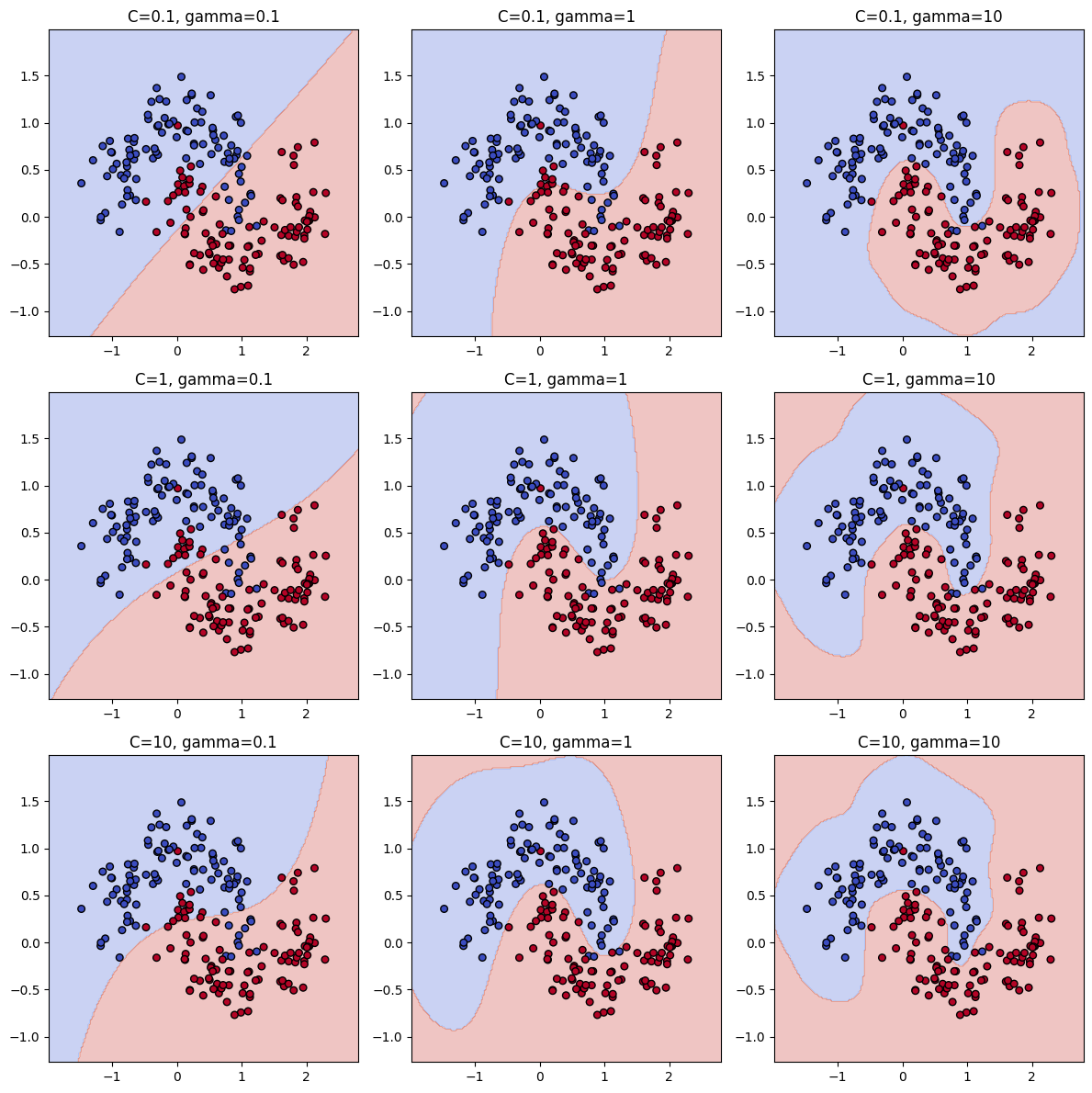
SVR
import numpy as np
import matplotlib.pyplot as plt
from sklearn.svm import SVR
# 샘플 데이터 생성
X = np.sort(5 * np.random.rand(100, 1), axis=0)
y = np.sin(X).ravel() + 0.2 * np.random.randn(100)
# C와 gamma 후보
C_values = [0.1, 1, 10]
gamma_values = [0.1, 1, 10]
plt.figure(figsize=(12, 12))
X_plot = np.linspace(0, 5, 100).reshape(-1, 1)
# 3x3 그리드로 그리기
for i, C in enumerate(C_values):
for j, gamma in enumerate(gamma_values):
svr = SVR(C=C, gamma=gamma)
svr.fit(X, y)
y_pred = svr.predict(X_plot)
plt.subplot(3, 3, i*3 + j + 1)
plt.scatter(X, y, color='darkorange', label='data')
plt.plot(X_plot, y_pred, color='navy', lw=2, label='SVR fit')
plt.title(f"C={C}, gamma={gamma}")
plt.ylim(-2, 2)
if i == 2 and j == 0:
plt.legend()
plt.tight_layout()
plt.show()
K-NN
- k ↑ (이웃 수 늘리기) → 분산 감소, 이웃이 많을수록 모델이 덜 민감
- 거리 가중 평균 사용
import numpy as np
from sklearn.datasets import make_moons
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import accuracy_score
import matplotlib.pyplot as plt
# 1. 데이터 생성
X, y = make_moons(n_samples=300, noise=0.25, random_state=42)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
# 2. 과대적합 K-NN (k=1)
knn_overfit = KNeighborsClassifier(n_neighbors=1)
knn_overfit.fit(X_train, y_train)
y_pred_overfit = knn_overfit.predict(X_test)
print("과대적합 K-NN (k=1) 정확도:", accuracy_score(y_test, y_pred_overfit))
# 3. 과대적합 해소 K-NN (k=15, 거리 가중치)
knn_regularized = KNeighborsClassifier(n_neighbors=15, weights='distance')
knn_regularized.fit(X_train, y_train)
y_pred_regularized = knn_regularized.predict(X_test)
print("과대적합 해소 K-NN (k=15, 거리 가중치) 정확도:", accuracy_score(y_test, y_pred_regularized))
# 4. 시각화 (가로로 비교)
def plot_knn_comparison(knn1, knn2, X, y, title1, title2):
fig, axes = plt.subplots(1, 2, figsize=(12,5)) # 가로 2개
x_min, x_max = X[:,0].min()-0.5, X[:,0].max()+0.5
y_min, y_max = X[:,1].min()-0.5, X[:,1].max()+0.5
xx, yy = np.meshgrid(np.linspace(x_min, x_max, 200),
np.linspace(y_min, y_max, 200))
for ax, knn, title in zip(axes, [knn1, knn2], [title1, title2]):
Z = knn.predict(np.c_[xx.ravel(), yy.ravel()]).reshape(xx.shape)
ax.contourf(xx, yy, Z, alpha=0.3, cmap=plt.cm.coolwarm)
ax.scatter(X[:,0], X[:,1], c=y, cmap=plt.cm.coolwarm, edgecolors='k')
ax.set_title(title)
plt.show()
plot_knn_comparison(
knn_overfit, knn_regularized, X, y,
"K-NN (k=1)", "K-NN (k=15)"
)
Decision Tree
- max_depth ↓ : 트리가 너무 깊어지면 학습 데이터에만 맞춤
- max_features ↓ : 일부 특징만 보고 분할하면 트리가 덜 복잡해짐
- max_leaf_nodes ↓ : 리프가 많으면 학습 데이터에 지나치게 맞춤
- min_samples_split ↑ : 너무 작은 수치로 나누면 트리가 깊어짐
- min_samples_leaf ↑ : 작은 노드가 생기는 걸 방지
- min_weight_fraction_leaf ↑ : 노드가 너무 작아지는 걸 방지
- min_impurity_decrease ↑ : 불순도 감소가 충분하지 않으면 분할하지 않음
- ccp_alpha ↑ : 트리 가지치기 강화
Random Forest
- n_estimators ↑ : 과적합 감소, 일반화 안정화
AdaBoost
- n_estimators ↓ : 이전 학습기의 오류를 다음 학습기가 학습 (모델이 학습 데이터에 과도하게 맞춰져 과대적합 발생)
- learning_rate ↓ : 너무 크면 한 학습기가 결과에 큰 영향을 주어 빠르게 학습 → 과대적합 위험이 증가
Gradient Boosting
- n_estimators ↓ : 이전 트리의 오류를 다음 트리가 학습 → 트리가 많을수록 과대적합 발생
- learning_rate ↓ : 너무 크면 한 학습기가 결과에 큰 영향을 주어 빠르게 학습
- subsample ↓ : 전체 데이터를 사용하지 않고 일부만 학습 → 모델의 분산 줄이고 과대적합 완화
- alpha ↓ : 이상치로 인한 과도한 학습 억제
- validation_fraction ↑ : 검증용 데이터가 충분히 있어야 학습 조기 종료 가능
XGBoost
- learning_rate ↓ : 낮출수록 트리가 조금씩 학습 → 과대적합 완화
- n_estimators ↓ : 부스팅 → 트리가 많을수록 과대적합 발생
- gamma ↑ : 노드를 분할하기 위해 필요한 최소 손실 감소량, 값이 크면 노드 분할 제한 → 과대적합 완화
- min_child_weight ↑ : 값이 작으면 노드가 쉽게 분할 → 과대적합
- subsample ↓ : 각 트리를 학습할 때 데이터 일부만 사용 → 분산 감소, 과대적합 완화
- colsample_bytree ↓ : 각 트리를 학습할 때 데이터 일부만 사용 → 분산 감소, 과대적합 완화
- colsample_bylevel ↓ : 각 레벨의 분할에서 컬럼 샘플링 비율 → 분산 감소, 과대적합 완화
- reg_alpha ↑ : 모델 복잡도를 낮추고, 작은 가중치를 0으로 만든다. (L1)
- reg_lambda ↑ : 트리의 리프(weight)를 학습할 때, 값이 너무 커지지 않도록 패널티 부여
심층신경망
- 네트워크 복잡도 제어
- 드롭아웃 : 학습 과정에서 일부 뉴런을 제거, 평가 단계에서는 모든 뉴런 활성화 → 훈련 속도만 감소
- 배치 정규화 : 각 층의 입력 분포가 변경되지 않도록 정규화
- 규제 강화 : 모델의 가중치를 규제, 손실 함수에 페널티 추가
- Early Stopping : 학습 중 성능이 개선되지 않으면 학습을 중지
나이브 베이즈
- alpha ↑ : alpha가 커질수록 모델이 더 평균적인 확률을 쓰게 되어 과대적합 완화
군집 모델 (Kmeans, 병합 군집)
- n_clusters ↓ : 너무 많이 잡아서 데이터에 너무 정확히 맞추는 경우 → 과대적합
차원축소
- PCA, AutoEncoder의 차원 수 감소 (더 적은 차원으로 표현해야 단순한 모델)
Gaussian Mixture Model (GMM)
- 복잡한 분포를 단순화
- 컴포넌트 수 ↓
- 공분산 형태 제한
베이지안 회귀 (Bayesian Regression)
- 사전 확률로 가중치 범위 제한
- Prior 분포를 강하게 설정
'개발 > Python' 카테고리의 다른 글
| 불균형 데이터 처리 (0) | 2025.10.08 |
|---|---|
| Batch Normalization vs Layer Normalization (0) | 2025.10.08 |
| 이미지 생성형 AI 모델 (0) | 2025.10.06 |
| 주요 합성곱 신경망 (0) | 2025.10.06 |
| 경사 하강법, 옵티마이저 (0) | 2025.10.06 |




댓글