적합도 검정 (Goodness of Fit Test)
목적 : 하나의 범주형 변수가 특정 분포(예: 균일분포, 정해진 비율 등)를 따르는지 확인
가정 : 기대도수가 충분히 커야 함(일반적으로 5 이상)
예시 : 주사위를 60번 던졌을 때 [8, 10, 9, 12, 11, 10] 번 나왔다면 → 이 주사위가 공정한지?
귀무가설(H₀) : 관측된 분포가 기대(이론) 분포와 동일하다.
대립가설(H₁) : 관측된 분포가 기대(이론) 분포와 다르다.
import numpy as np
from scipy.stats import chisquare
# 관측값 (주사위 결과)
observed = np.array([8, 10, 9, 12, 11, 10])
# 기대값 (공정한 주사위 -> 60번 던지면 각 면 10번 기대, 스케일 일치 필요)
expected = np.array([10, 10, 10, 10, 10, 10])
chi2, p = chisquare(f_obs=observed, f_exp=expected)
print("카이제곱 통계량:", chi2) # 1.0
print("p-value:", p) # 0.9625657732472964독립성 검정 (Test of Independence)
목적 : 두 범주형 변수 간에 독립인지 / 연관성이 있는지 확인
데이터 형태 : 교차표 (contingency table)
예시 : 성별(남/여)과 흡연 여부(흡연/비흡연) 사이에 연관성이 있는지 확인
귀무가설(H₀) : 두 변수는 서로 독립이다 (관계가 없다)
대립가설(H₁) : 두 변수는 서로 독립이 아니다 (관계가 있다)
import pandas as pd
from scipy.stats import chi2_contingency
# 성별(행) vs 흡연여부(열) 교차표
data = pd.DataFrame([
[40, 10], # 남자 (흡연, 비흡연)
[30, 20] # 여자
], columns=["흡연", "비흡연"], index=["남자", "여자"])
chi2, p, dof, expected = chi2_contingency(data)
print("카이제곱 통계량:", chi2)
print("p-value:", p)
print("자유도:", dof)
print("기대도수:\n", expected)
correction
- 기본값 True
- 자유도가 1일 때 Yates 연속성 보정을 적용함 (2×2 분할표, 카이제곱 독립성 검정에만 사용)
- 이 보정은 관측값을 기대값 쪽으로 0.5 만큼 이동하여 계산
- 2×2 표는 표본 수가 작으면 결과가 실제보다 더 민감하게(과대하게) 나올 수 있음 → 이를 완화하기 위한 보정
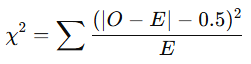
동질성 검정 (Test of Homogeneity)
목적 : 여러 집단의 분포가 동일한지 비교
독립성 검정과 차이 : 수학적으로는 같은 방식(교차표 + 카이제곱), 연구 목적이 다름
- 독립성 검정 → "두 변수 간 관계가 있는가?"
- 동질성 검정 → "여러 집단의 분포가 동일한가?"
예시: 지역별(서울, 부산, 대구)로 선호하는 과일(사과, 바나나, 포도)의 분포가 같은지?
귀무가설(H₀) : 모든 집단의 분포가 동일하다.
대립가설(H₁) : 적어도 한 집단의 분포가 다르다.
import pandas as pd
from scipy.stats import chi2_contingency
# 지역별 과일 선호도
data = pd.DataFrame([
[30, 10, 10], # 서울
[20, 20, 10], # 부산
[25, 15, 10] # 대구
], columns=["사과", "바나나", "포도"], index=["서울", "부산", "대구"])
chi2, p, dof, expected = chi2_contingency(data)
print("카이제곱 통계량:", chi2)
print("p-value:", p)
print("자유도:", dof)
print("기대도수:\n", expected)

실제 관측값과 기대값의 차이(잔차)가 커질수록 카이제곱 값이 커진다.
- χ² 값이 작다
→ 관측값과 기대값이 비슷하다
→ 귀무가설(H₀: 분포가 같다, 독립이다, 동질하다)을 기각하기 어렵다 - χ² 값이 크다
→ 관측값과 기대값이 많이 다르다
→ 귀무가설을 기각할 가능성이 크다 → "차이가 있다 / 관계가 있다 / 분포가 다르다"라고 해석.
'개발 > Python' 카테고리의 다른 글
| datetime (0) | 2025.09.14 |
|---|---|
| LogisticRegression Hyper Parameters and Attributes (0) | 2025.09.14 |
| DecisionTree Hyper Parameters and Attributes (0) | 2025.09.08 |
| 검정 통계량 T, 평균의 차이와 신뢰구간 (0) | 2025.09.08 |
| 병합적 군집분석 계산 방법 비교 (linkage) (0) | 2025.09.08 |


댓글