N = 데이터의 수, M = Feature의 수
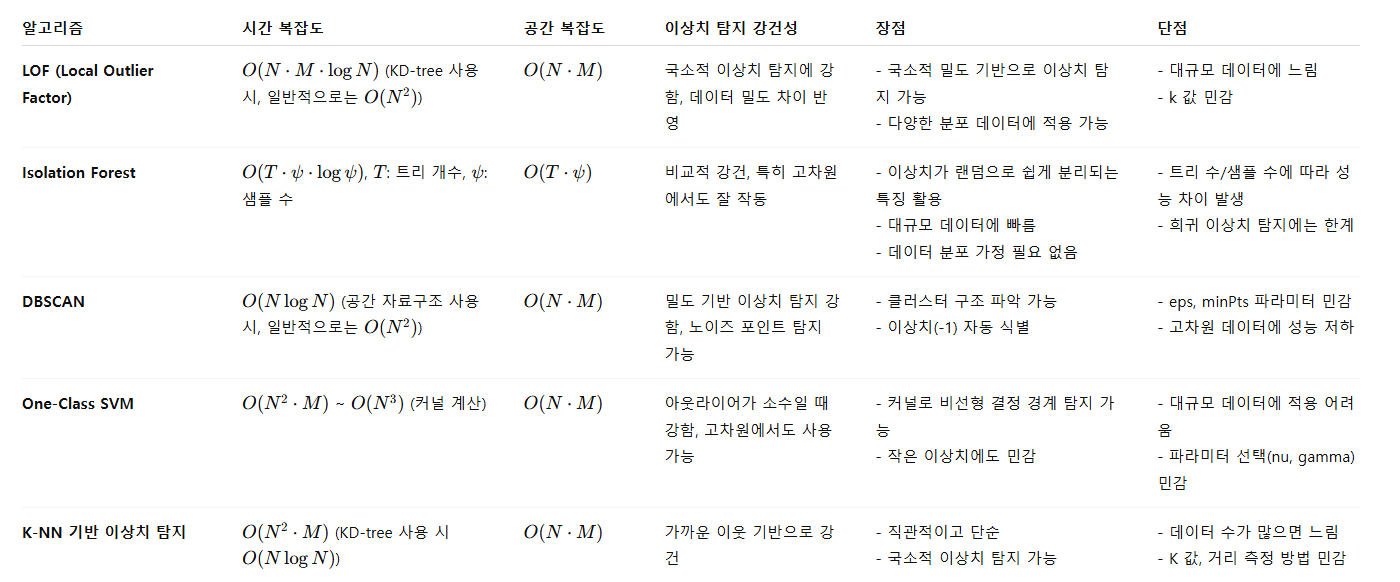
LOF (Local Outlier Factor)
- 이웃의 평균 밀도 대비 자기 자신이 얼마나 밀도가 낮은지 측정함으로써 이상치를 판단
- 거리 기반 방법의 단점 보완
- 고차원 데이터(M이 큰 경우)에서는 차원 축소(PCA), 특징 선택 등을 선행
- 모든 데이터를 고려하지 않고, 해당 포인트의 주변 데이터만 이용하여 이상치 탐지
원리
1. k-최근접 이웃(k-NN)으로 지역 밀도 추정
- 각 데이터 포인트 p에 대해 거리 기반으로 가까운 k개 이웃을 탐색
- 이를 기반으로 샘플의 밀도가 이웃들보다 현저히 낮은 경우 해당 샘플을 이상치(outlier)로 간주.
2. 도달 거리(Reachability Distance) 계산
- 근접 이웃 하나 o에 대해 너무 가까운 이웃이 있는 경우 과도한 이상치 판정을 막기 위해 거리 값을 보정

3. 지역 밀도(Local Reachability Density, LRD) 계산
의 주변 밀도는 이웃까지의 도달 거리 평균의 역수로 정의

4. 주변 이웃과의 밀도 비율 계산 → LOF 점수
- 각 샘플의 이상 점수는 Local Outlier Factor라고 불리며, 해당 샘플의 주변 밀도와의 지역적 편차를 측정
- 이 점수는 지역적(local) 특성을 갖고 있어, 객체가 그 주변 이웃에 비해 얼마나 고립되어 있는지를 나타냄
- 이웃의 평균 밀도 대비 자기 자신이 얼마나 밀도가 낮은지 측정함으로써 이상치를 판단

- LOF ≈ 1 : 정상 데이터
- LOF > 1 : 이상치 가능성 → 1.5 이상부터 강한 이상치로 보는 경우 많음
- LOF < 1 : 이웃보다 더 밀도 높은 구역 (test data가 cluster 내부에 깊게 위치)
시간 복잡도
- O(N2 * M)
- KD-Tree 사용, 저차원 (M << N) : O(N * logN * M)
공간 복잡도
- KD-Tree를 사용하면 : O(N * M)
- 모든 거리를 미리 계산하면 : O(N2)
장점
- 데이터 분포나 밀도에 대한 가정 불필요 비모수적 비지도 학습 → 정규분포 / 가우시안 가정 불필요
- 지역 기반(local) 이상치 탐지에 강함 전체가 아닌 주변 이웃과 직접 비교 → 군집마다 밀도가 다른 경우 특히 유리
- 군집형 데이터에서도 성능 우수 다양한 밀도(cluster) 구조를 가진 데이터에서 글로벌 threshold 기반 방법보다 정확
- 이상치 정도를 수치화(연속 점수) 단순 이진 판단이 아니라 LOF 점수로 이상치의 강도 측정 가능
- 잡음(edge case)에도 민감하게 대응, 고립된 포인트를 잘 탐지
단점
- 거리 기반 → 차원의 저주에 취약 고차원에서 거리 분리도가 떨어져 성능 하락
- k 선택에 민감, 너무 작으면 local noise에 취약, 너무 크면 global화되어 이상치 누락
- 시간 복잡도 높음 k-NN 탐색 필요 → 일반적으로, 데이터가 크면 성능 저하
- 밀도가 균일한 데이터에서 부정확 지역 밀도 차이가 없다면 LOF 점수도 1 근처에 모임
- 파라미터 조정 필요 (contamination, k, metric → 신뢰도에 영향)
- 이상치가 클러스터를 형성하면 탐지 어려움 (주변 밀도와 유사하면 이상치로 판단하지 못함)

Isolation Forest
- 랜덤 분할로 데이터를 고립시키며, 고립되는 데 걸리는 깊이로 이상치를 판단하는 앙상블 기반 알고리즘
- 단일 Tree의 결과가 불안정(편향/분산)하여 Bagging을 응용하여 이상치 여부를 나타내는 점수의 신뢰성을 높임.
- 특이치 탐지보다 이상치 탐지에 적합
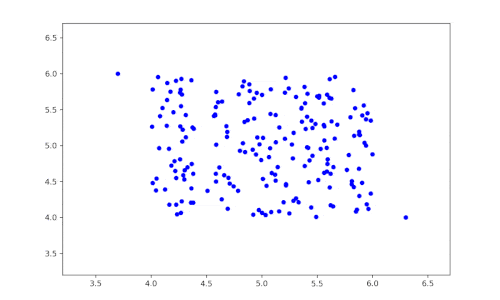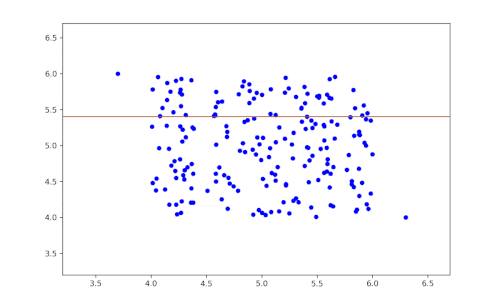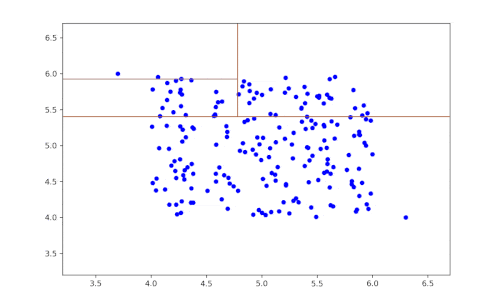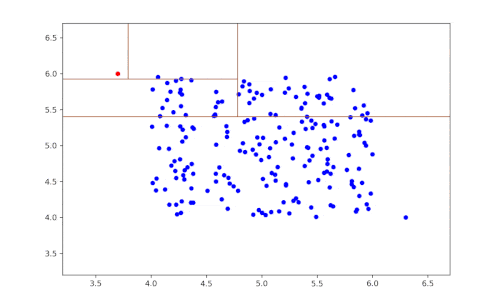
원리
- 이상치는 정상 데이터보다 쉽게 고립된다. → 고립되는 데 필요한 분기 수(트리 깊이)가 작다.
- 즉, 데이터 공간을 무작위로 분할하면서 특정 데이터 포인트가 얼마나 빨리 고립되는지 측정
1. 무작위 분할 기반 Tree(Isolation Tree, iTree) 생성
- 데이터의 특정 Feature 하나를 랜덤 선택
- 해당 Feature에서 임의의 값으로 분할
- 계속 분할하면서 Leaf Node에 한 개의 데이터만 남을 때까지 진행
- 이 과정에서 이상치는 다른 점들과 멀리 떨어져 있으므로 몇 번 나누지 않아도 혼자 분리됨
→ 얕은 깊이에서 고립 = 이상치
- 정상치는 많은 점들과 섞여 있어 여러 번 분할되어야 떨어져 나옴
→ 깊은 노드에 위치 = 정상
2. 여러 iTree를 만든다 (앙상블)
- 개별 트리만으로는 랜덤성 때문에 불안정
- n_estimators 개 트리를 만들고 평균 깊이를 사용
3. 고립 난이도 평균값으로 Score 계산
- 평균 깊이 E(h(x)) 를 이용해 이상치 점수(Anomaly Score)를 계산
- 점수가 1에 가까울수록 → 이상치
- 점수가 0에 가까울수록 → 정상
시간 복잡도
- O(T * M * N * logN), T = 트리의 개수
공간 복잡도
- 최대 깊이가 ψ인 이진트리의 공간복잡도 = O(ψ)
장점
- 데이터의 분포나 밀도에 대한 가정을 하지 않음 (다양한 데이터 유형 적용, 비지도 학습)
- 거리 기반 알고리즘(LOF, k-NN)보다 고차원 데이터에서 성능 저하가 상대적으로 적고 효율적인 알고리즘
- 빠른 속도 시간 복잡도 O(n log n), 데이터가 커도 스케일링 잘 됨
- 앙상블 기반으로 안정성 확보, 랜덤 트리 여러 개로 결과 신뢰성 향상
- 이상치 점수 제공 이진 판단뿐 아니라 "이상치 정도" 평가 가능
단점
- 군집형(Local) 이상치 탐지에 약함 → 군집 내부의 미묘한 이상치 탐지가 어려움
- 랜덤성에 의한 결과 편차 트리 개수가 적으면 불안정
- 카테고리 데이터 처리 약함, 수치형 기준으로 설계됨 → 전처리 필요
- 복잡한 비선형 경계 탐지 한계, SVM 등보다 경계가 단순하게 형성됨
- 초기 파라미터 설정 영향 큼 → max_samples, contamination 설정에 민감


DBSCAN
- 두 가지 주요 파라미터인 epsilon ε (주변 반경)과 min_samples (최소 샘플 수)를 설정하여 군집을 형성
- 데이터의 지역적인 구조(지역적인 밀집 정도)를 이용
- 주변 데이터에서 멀어지는 데이터의 특징을 찾아서 분류하여 특이점을 발견
- 밀도가 낮은 지역의 데이터 포인트를 이상치로 간주

원리
- ε : 주변 반경
- min_samples : 핵심 포인트(Core Point) 판정 기준
ㄴ 최소 이웃의 수에 자기 자신을 포함한다.
ㄴ ex. 최소 이웃 수에 자기 자신을 포함하지 않고 코어 포인트가 되기 위한 이웃의 수가 9라면 10을 설정해야 한다.
1. 모든 포인트에 대해 ε 반경 안에 이웃이 몇 개 있는지 확인
2. 각 포인트를 3가지 유형으로 분류
| 유형 | 조건 | 역할 |
| Core Point | 주변 영역 내에 최소 데이터 개수 이상의 타 데이터를 가지고 있을 경우 이웃 수 ≥ min_samples |
군집의 중심 → 군집 확장 가능 |
| Border Point | 주변 영역 내에 최소 개수 이상의 이웃 포인터를 가지고 있지 않지만 핵심 포인트를 이웃으로 가짐 ε 반경 내 이웃 수 < min_samples |
군집의 경계, 확장 불가능 군집의 외곽을 형성 |
| Noise Point | 최소 데이터 개수 이상의 이웃 포인터를 가지고 있지 않으며, 핵심 포인트도 이웃 포인트로 가지고 있지 않음 어떤 Core Point의 이웃도 아님 |
군집에 속하지 않음 label = -1인 데이터 |
* Neighbor Point : 주변 영역 내에 위치한 타 데이터
- 군집 확장은 Core Point들 간의 연결성 으로 이루어짐
- Border Point는 군집에 속하지만 다른 Border Point와 직접 연결되어 군집을 만들 수 없음
3. Core Point에서 시작하여 직접 도달(Directly Reachable) 가능한 Core Point들을 계속 연결
→ 하나의 군집 형성
4. 연결이 끝나면 Core에 접한 Border Point를 해당 군집에 포함
시간 복잡도
- O(N2 * M)
- KD-Tree, Ball-Tree 사용, 저차원 (M << N) : O(N * logN)
공간 복잡도
- 원본 데이터 저장 : O(N * M)
- 거리 행렬 사용 시 : O(N2)
장점
- 군집 개수를 지정할 필요 없음
- 비선형/복잡한 형태 군집 탐지 가능 (원형, 반달 모양, 직선 경계가 아닌 데이터)
- 이상치 (Outlier = 군집에 속하지 않는 Noise Point) 탐지 가능
- 밀도 기반 군집화 → 서로 다른 밀도를 가진 군집도 어느 정도 탐지 가능
- 간단한 알고리즘 구조 → ε, min_samples 두 개 파라미터만 설정
단점
- 파라미터 민감성, 데이터 분포에 따라 최적 값 찾기가 어려움
- 데이터의 특성을 파악하여 군집 밀도, 최소 데이터 수 등 파라미터를 직접 조정
- 고차원 데이터에서 성능 저하 (KD-Tree, Ball-Tree 같은 공간 자료구조 효율 ↓)
- 대규모 데이터셋 취약
- 새로운 데이터 예측 불가 (fit → predict 미지원)
- 새로운 포인트를 기존 군집에 할당하기 어려움
- 밀도가 매우 다른 군집 처리 어려움 (ε와 min_samples는 전역 기준 → 밀도 차이가 큰 군집에는 부적합)

One-Class SVM
- 정상 데이터만 보고 학습해서, 새로운 데이터가 정상 범위에 속하는지 판단하는 비지도 이상치 탐지
- 데이터 공간에 존재하는 경계를 표현 → 가장 큰 마진으로 갖는 경계를 찾음
- 샘플을 고차원에 매핑 → 클래스 분리 → 원본 공간의 영역에 존재하지 않는다면 이상치
- 이상치 탐지보다는 특이치 탐지에 더 잘 맞음

원리
1. 데이터를 고차원 특징 공간으로 매핑
- 커널 트릭을 사용해 데이터를 고차원으로 변환
- 선형적으로 분리 가능한 형태로 바꿈
2. 정상 데이터를 감싸는 경계 결정
- 데이터 포인트들을 원본 공간에서 영역으로 감싸는 초평면(hyperplane)을 찾음
- 마진(Margin)을 최대화하여, 가능한 넓은 영역을 정상 데이터로 포함
3. 새로운 샘플 평가
- 결정 함수(Decision function)로 경계 내부/외부 판단
- 내부 → 정상, 외부 → 이상치
시간 복잡도
- O(N3)
- 커널 행렬 사용 : O(N2 * M)
공간 복잡도
- 커널 행렬 저장: O(N²)
- 데이터 저장: O(N * M)
- 전체 공간 복잡도 = O(N² + N * M)
장점
- 비지도 학습 기반
- 고차원 공간에서도 데이터 영역을 정의할 수 있음.
- 커널 트릭(Kernel Trick)을 사용하면 비선형 경계 학습 가능
- 데이터 분포 가정 불필요 → 특정 분포(정규분포 등)에 의존하지 않고, 데이터의 경계만 학습.
- 이상치와 정상치 구분 명확
- 오류 데이터에 대한 영향이 적음
- 정규화된 이상치 점수 제공: 결정 함수 값이 0보다 작으면 이상치
단점
- 대규모 데이터에 부적합 → 학습 시 커널 행렬과 QP 최적화 때문에 계산 비용과 메모리 사용량이 급증
- 하이퍼파라미터 민감 → nu, gamma, kernel 등의 설정에 따라 결과가 크게 달라짐.
- 희소하거나 복잡한 데이터에 약함 → 데이터 밀도가 낮거나 구조가 복잡하면 결정 경계가 부정확해짐.
- 이상치 점수 해석이 상대적 → 확률적 의미가 명확하지 않고, 이상치 여부가 상대적임.
- 학습 속도가 느리고, 해석이 까다로움.
그 외
- PCA의 일정 수준이상의 성분을 선택한 후, 다시 역변환 했을 때 원래 데이터의 차이가 큰 데이터 포인트가 이상치
- 사분위 범위 기반 이상치 탐지
- 코사인 거리를 활용한 이상치 탐지
예제 1
다음 데이터에 대해 LOF를 이용하여 Noise 행을 판별하라.
import pandas as pd
import numpy as np
np.random.seed(1234)
# 정상 데이터 100개 (2차원)
normal_data = np.random.normal(loc=0, scale=1, size=(100, 2))
# 이상치 데이터 5개 (멀리 떨어진 위치)
outlier_data = np.random.normal(loc=8, scale=0.5, size=(5, 2))
# 합치기
data = np.vstack([normal_data, outlier_data])
# DataFrame 생성
df = pd.DataFrame(data, columns=['feature1', 'feature2'])
# data shuffle
df = df.sample(frac=1).reset_index(drop=True)
df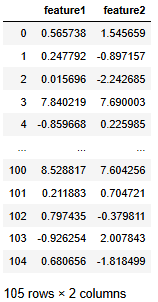
시각화하면 다음과 같다.
import matplotlib.pyplot as plt
# 시각화
plt.figure(figsize=(8, 6))
# 정상 데이터
plt.scatter(df.loc[:, 'feature1'],
df.loc[:, 'feature2'],
c='blue', label='Normal', alpha=0.6)
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.title('All Data')
plt.legend()
plt.grid(True)
plt.show()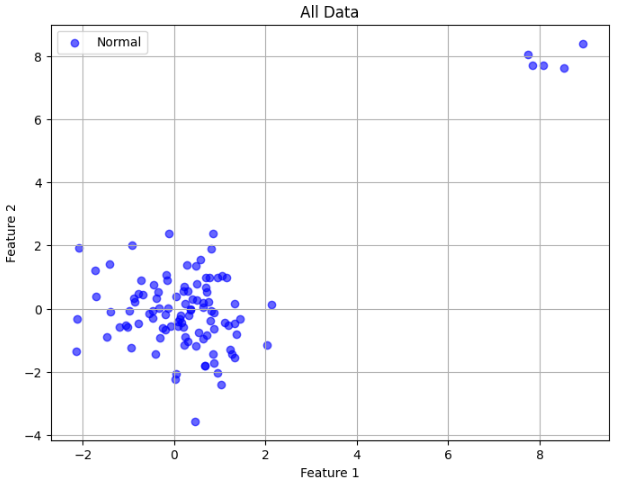
LocalOutlierFactor를 이용해서 -1인 경우를 이상치로 분류할 수 있다.
n_neighbors - 최근접 이웃 개수. 만약 이 값이 샘플 수보다 크면 전체 샘플이 사용된다.
contamination - 데이터셋에 존재하는 이상치 비율. fit() 시 decision 함수 임계값 설정에 사용 ('auto' = 자동 설정)
novelty=False (default)인 경우, 완전한 비지도 학습, fit 시 사용한 데이터에 대해서만 이상치 점수를 계산한다.
from sklearn.neighbors import LocalOutlierFactor
lof = LocalOutlierFactor(n_neighbors=20, contamination=0.05, novelty=False)
y_pred = lof.fit_predict(df) # -1: 이상치
df['outlier'] = y_pred
novelty=True인 경우 학습 시 정상 패턴을 학습하고, 이후 추가된 새로운 샘플이 정상 범위에 있는지 여부를 예측한다.
from sklearn.neighbors import LocalOutlierFactor
lof = LocalOutlierFactor(n_neighbors=20, contamination=0.05, novelty=True)
y_pred = lof.fit(df).predict(df) # -1: 이상치
df['outlier'] = y_pred
이상치로 분류된 데이터를 그려면 다음과 같다.
import matplotlib.pyplot as plt
# 시각화
plt.figure(figsize=(8, 6))
# 정상 데이터
plt.scatter(df.loc[df['outlier'] == 1, 'feature1'],
df.loc[df['outlier'] == 1, 'feature2'],
c='blue', label='Normal', alpha=0.6)
# 이상치 데이터
plt.scatter(df.loc[df['outlier'] == -1, 'feature1'],
df.loc[df['outlier'] == -1, 'feature2'],
c='red', label='Outlier', marker='x', s=100)
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.title('Local Outlier Factor (LOF) - Outlier Detection')
plt.legend()
plt.grid(True)
plt.show()
6개의 이상치 중 임의로 만든 5개의 이상치가 포함되어 있는 것을 알 수 있다.
그리고 이상치로 판단되는 행은 아래와 같은 방법으로 제거할 수 있다.
normal = df[df['outlier'] != -1].copy()예제 2
다음 데이터에 대해 데이터의 중심과 코사인 거리를 이용하여 이상치를 제거하라
(이상치 = 코사인 거리 < q1 - 1.5 * iqr 또는 코사인 거리 > q3 + 1.5 * iqr)

import pandas as pd
import numpy as np
np.random.seed(1234)
data = np.random.rand(100, 3)
columns = ['feature1', 'feature2', 'feature3']
df = pd.DataFrame(data, columns=columns)
df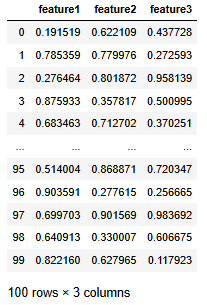
먼저 데이터의 중심을 구한다.
center = np.array(df.mean(axis=0))
center
그러면 데이터의 중심의 norm은 다음과 같이 구할 수 있다.
c_norm = np.sqrt(np.sum(center ** 2))
c_norm
이제 코사인 거리 공식에 해당되는 값을 대입하면 된다.
child = (center[0] * df['feature1'] + center[1] * df['feature2'] + center[2] * df['feature3'])
parent = (c_norm * np.sqrt(df['feature1'] ** 2 + df['feature2'] ** 2 + df['feature3'] ** 2))
cos_distances = 1 - (child / parent)
cos_distances
코사인 거리를 데이터 프레임에 추가하고 주어진 이상치 판단 공식에 대입하면 2개의 이상치를 제거할 수 있다.
df['cos_dist'] = cos_distances
q1 = df['cos_dist'].quantile(0.25)
q3 = df['cos_dist'].quantile(0.75)
iqr = q3 - q1
df_del = df[(df['cos_dist'] >= q1 - 1.5 * iqr) & (df['cos_dist'] <= q3 + 1.5 * iqr)].copy()
df_del
sklearn.metrics.pairwise의 cosine_distances로 코사인 거리를 구할 수도 있다.
from sklearn.metrics.pairwise import cosine_distances
center = df.mean().values.reshape(1, -1)
cos_distances = cosine_distances(df.values, center).flatten()
cos_distances
예제 3
다음 데이터에 대해 분산 중 80% 이상을 설명할 수 있는 최소 차원의 수로 사영한 후, 데이터를 다시 복원하라
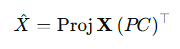
이후 원본 데이터와 복원된 데이터의 유클리드 거리의 제곱을 구해서 3.5보다 큰 값을 이상치로 판단하고 제거하라.
import pandas as pd
import numpy as np
np.random.seed(1234)
data = np.random.rand(100, 10)
columns = ['X1', 'X2', 'X3', 'X4', 'X5', 'X6', 'X7', 'X8', 'X9', 'X10']
df = pd.DataFrame(data, columns=columns)
df
80% 이상을 설명하는 주성분을 찾기 위해 n_components를 0.8로 설정하였다.
from sklearn.decomposition import PCA
pca = PCA(svd_solver='full', n_components=0.8)
pca.fit(df)
해당 차원으로 사영된 데이터는 fit_transform으로 구할 수 있다.
shape를 확인해보면 80% 이상을 설명하는 주성분은 8개(차원 = M)임을 알 수 있다.
proj = pca.fit_transform(df)
proj.shape
(PC)^T, 주성분 행렬의 전치 행렬은 components_에서 얻을 수 있다. (M = 8)
pc_t = pca.components_
pc_t.shape
numpy의 matmul을 이용해 x_hat을 계산하면 된다. → (100, 8) x (8, 10)
x_hat = np.matmul(proj, pc_t)
x_hat = pd.DataFrame(x_hat, columns=df.columns)
x_hat
df['dist'] = ((df - x_hat) ** 2).sum(axis=1)
df
2개의 이상치가 제거된 것을 알 수 있다.
df_del = df[df['dist'] <= 3.5].copy()
df_del.shape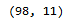
예제 4
IQR을 활용한 이상치 대치
import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split
# -------------------------------
# 1. 예시 DataFrame 만들기
# -------------------------------
np.random.seed(42)
# 정상 분포 데이터 100개 + 이상치 몇 개 추가
data = {
"value": np.concatenate([
np.random.normal(50, 10, 100),
np.array([5, 150]) # 명확한 이상치
])
}
df = pd.DataFrame(data)
print("원본 데이터 요약:")
print(df.describe())
# -------------------------------
# 2. train / test 분리
# -------------------------------
train_df, test_df = train_test_split(df, test_size=0.2, random_state=42)
print("\nTrain 크기:", train_df.shape)
print("Test 크기:", test_df.shape)
# -------------------------------
# 3. Train에서만 IQR 계산
# -------------------------------
Q1 = train_df["value"].quantile(0.25)
Q3 = train_df["value"].quantile(0.75)
IQR = Q3 - Q1
lower = Q1 - 1.5 * IQR
upper = Q3 + 1.5 * IQR
print("\nIQR lower:", lower)
print("IQR upper:", upper)
# -------------------------------
# 4. train/test 모두 clip (Train에서 계산한 값 사용)
# -------------------------------
train_df["value_clipped"] = train_df["value"].clip(lower, upper)
test_df["value_clipped"] = test_df["value"].clip(lower, upper)
# -------------------------------
# 5. 결과 확인
# -------------------------------
print("\n=== Train Before/After ===")
print(train_df[["value", "value_clipped"]].head())
print("\n=== Test Before/After ===")
print(test_df[["value", "value_clipped"]].head())
'개발 > Python' 카테고리의 다른 글
| 선형회귀모형의 변수 선택 (후진제거법, 전진선택법) (1) | 2025.08.14 |
|---|---|
| 병합적 군집분석 결과를 다른 데이터 샘플에 적용하기 (3) | 2025.08.13 |
| 그룹 별 변수들의 차이 비교 (일원분산분석 vs Kruskal-Wallis 검정) (4) | 2025.08.10 |
| Pandas 전처리 - 결측치 처리 (1) | 2025.08.10 |
| 빅데이터분석기사 실기 체험 문제풀이 (0) | 2025.06.06 |




댓글