사회연결망 분석 (Social Network Analysis, SNA)
- 사람, 조직, 객체 등 사회적 주체들 간의 관계(연결)를 분석해 구조적 패턴을 이해하는 방법
집합론적 방법 (Set-theoretic Approach)
- 노드 집합 V와 노드 간의 관계 집합 R ⊆ V×V로 네트워크를 정의
- 각 객체들 간의 관계를 쌍으로 표현
집합 V = {A, B, C}
관계 R = {(A, B), (A, C), (B, C)}
그래프 이론 방법 (Graph-theoretic Approach)
- 네트워크를 그래프로 모델링
- G = (V, E)
행렬 방법 (Matrix Approach)
- 1-mode data : 노드들이 동일한 종류(한 집합)일 때 만드는 네트워크 (정방 행렬)
- 2-mode data : 두 종류의 서로 다른 노드 집합을 포함 (직사각형 행렬)
- 준연결망 : semi-network, 2-mode data를 1-mode data처럼 분석할 수 있도록 변환한 형태
| | A | B | C |
| A | 0 | 1 | 0 |
| B | 1 | 0 | 1 |
| C | 0 | 1 | 0 |
| | X | Y |
| A | 1 | 0 |
| B | 1 | 1 |
| C | 0 | 1 |
A와 B는 모두 X에 참여 → 연결(1)
B와 C는 모두 Y에 참여 → 연결(1)
A와 C는 함께 참여한 모임 없음 → 0연결 중심성 (Degree Centrality)
- 한 노드가 가지고 있는 직접 연결 수를 기반으로 영향력을 판단하는 지표.
- 연결이 많을수록 중심성이 높다.
- 연결 중심성이 높다 → 네트워크 내에서 더 많은 관계를 맺는다.
- 노드 간의 거리를 고려하진 않음.
- SNS에서 "팔로워 수가 많다 = 영향력 있다"와 비슷한 개념.
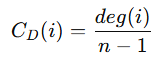
A — B — C — D
A: 1
B: 2
C: 2
D: 1
→ B와 C가 가장 중심적 노드
근접 중심성 (Closeness Centrality)
- 한 노드가 네트워크의 모든 다른 노드들과 얼마나 가까운지 측정하는 지표
- 정보를 얼마나 빠르게 퍼뜨릴 수 있는가를 나타내는 지표
- 근접 중심성이 높으면 네트워크의 중앙에 위치하게 된다.

A — B — C — D
A: (0,1,2,3) → 총 6
B: (1,0,1,2) → 총 4
C: (2,1,0,1) → 총 4
D: (3,2,1,0) → 총 6
→ 근접 중심성: B = C > A = D
→ B와 C가 네트워크 전체에 더 빨리 도달 가능
매개 중심성 (Betweenness Centrality)
- 노드가 다른 노드 쌍 사이의 최다 경로를 얼마나 많이 통과하는지를 측정하는 지표
- 연결망 내의 다른 노드들 사이의 최다 경로 위에 위치할수록 중심성이 높아진다.
- 정보 흐름의 중개자 역할
- 네트워크에서 가교 역할
- 어떤 노드를 제거하면 네트워크가 얼마나 단절되는지 판단 가능

A — B — C — D
B는 A ↔ C, A ↔ D 경로에서 반드시 거침
C도 B와 동일한 역할
A, D는 중개 역할 없음
→ 매개 중심성: B = C > A = D
위세 중심성 (Eigenvector Centrality)
- 연결이 많은 노드가 중요하다(Degree)에서 확장하여 중요한 노드와 연결되어 있으면 그 노드도 중요하다는 개념
- 위세가 높은 사람들과 관계가 많을수록 자신의 위세가 높아진다.
- 행렬 A (인접행렬)에 대해 Ax = λx를 만족하는 고유벡터 x의 값이 중심성 점수
- 단순한 연결 수보다 중요한 노드들과 얼마나 연결되어 있는가가 더 중요
- 위세가 높은 노드들과 관계가 많을수록 자신의 위세가 증가
- 보나사치 (Bonacich) 권력지수
- 구글의 PageRank
A — B — C
|
D
연결 수는 C가 가장 많지만
C는 아무도 중요한 노드와 연결되지 않음
B는 C와 연결되었고, A도 연결됨
A도 B를 통해 C와 연결됨
실제 eigenvector 중심성의 순위
B > A > C > D (네트워크 구조에 따라 다를 수 있음)

댓글