시계열 분석 (Time Series Analysis)
- 시간의 흐름에 따라 수집된 데이터를 분석해 패턴을 이해하고 미래를 예측하는 통계, 머신러닝 방법
- 일반적인 시계열 분석은 외부 변수를 다루지 않는다.
- 시계열 분석의 주 목적은 자체 시계열 내부 구조 분석 및 미래 예측
1) 추세 (Trend) - 시간이 지날수록 전체적으로 증가,감소하는 장기 변화 (인구 증가, 물가 상승)
2) 계절성 (Seasonality) - 일정 주기로 반복되는 패턴 (여름에 아이스크림 판매 증가, 월별 전기 사용량 패턴)
3) 순환(Cycle) - 경제/사회적 요인 등으로 길고 불규칙하게 반복되는 패턴 (경기 침체 → 회복 → 호황)
4) 불규칙(Noise) - 예측 불가능한 random 변동
시계열 자료
- 시간의 흐름에 따라 관찰된 값
- 시계열 분석으로 미래의 값 예측, 경향, 주기 계절성 파악
정상성 (stationarity)
- 시계열 데이터의 통계적 특성이 시간에 따라 변하지 않는 성질
- 정상성을 보이는 시계열은 추세나 계절성이 없다.
정상 시계열 (Stationary Time Series)
- 시간에 따라 통계적 성질이 변하지 않는 시계열
- 어떤 시점에서 평균과 분산이 동일
- 특정한 시차의 길이를 갖는 자기공분산이 동일
- 항상 그 평균값으로 회귀하려는 경향이 있으며, 그 평균값 주변에서의 변동은 대체로 일정한 폭을 가진다.
1) 평균이 일정할 경우
- 모든 시점에 대해 일정한 평균
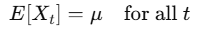
- 그렇지 않으면 차분을 통해 정상화 (차분 : 현시점 자료에서 전 시점 자료를 빼는 것)
- 평균이 일정하지 않은 경우 (추세 존재) → 차분(differencing)
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# -----------------------------
# 1. 비정상 시계열 생성 (평균 증가)
# -----------------------------
np.random.seed(42)
n = 100
time = pd.date_range(start='2025-01-01', periods=n, freq='D')
# 선형 추세 + 랜덤 노이즈
data = 0.5 * np.arange(n) + np.random.normal(scale=1.0, size=n)
ts = pd.DataFrame({'value': data}, index=time)
# -----------------------------
# 2. 시계열 시각화
# -----------------------------
plt.figure(figsize=(10,4))
plt.plot(ts, label='Original (Non-Stationary)')
plt.title("Non-Stationary Time Series")
plt.legend()
plt.show()
# -----------------------------
# 3. 차분 적용 (1차 차분)
# -----------------------------
ts_diff = ts.diff().dropna()
plt.figure(figsize=(10,4))
plt.plot(ts_diff, label='1st Difference (Stationary)')
plt.title("after")
plt.legend()
plt.show()
# -----------------------------
# 4. 평균 확인
# -----------------------------
print("원본 시계열 평균:", ts['value'].mean())
print("차분 시계열 평균:", ts_diff['value'].mean())
2) 분산이 일정
- 시점에 의존하지 않고 분산 일정

- 변환을 통해 정상화
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import boxcox
# -----------------------------
# 1. 비정상 시계열 생성 (분산 증가)
# -----------------------------
np.random.seed(42)
n = 100
time = pd.date_range(start='2025-01-01', periods=n, freq='D')
# 평균은 일정, 분산이 시간에 따라 증가
data = np.random.normal(loc=10, scale=np.linspace(1, 10, n)) # 분산 점점 증가
ts = pd.DataFrame({'value': data}, index=time)
# -----------------------------
# 2. 원본 시계열 시각화
# -----------------------------
plt.figure(figsize=(10,4))
plt.plot(ts, label='Original (Non-Stationary Variance)')
plt.title("Non-Stationary Time Series")
plt.legend()
plt.show()
# -----------------------------
# 3. 로그 변환으로 분산 안정화
# -----------------------------
ts['log_value'] = np.log(ts['value'] - ts['value'].min() + 1) # 음수 방지
plt.figure(figsize=(10,4))
plt.plot(ts['log_value'], label='Log Transformed')
plt.title("log transformation")
plt.legend()
plt.show()
# -----------------------------
# 4. 차분 적용 (1차 차분) -> 평균도 일정하게
# -----------------------------
ts['log_diff'] = ts['log_value'].diff().dropna()
plt.figure(figsize=(10,4))
plt.plot(ts['log_diff'], label='1st Difference (Stationary)')
plt.title("log transformation + diff")
plt.legend()
plt.show()
# -----------------------------
# 5. 평균, 분산 확인
# -----------------------------
print("원본 시계열 분산:", ts['value'].var())
print("로그 변환 후 분산:", ts['log_value'].var())
print("차분 + 로그 변환 후 분산:", ts['log_diff'].var())
3) 공분산
- 자기공분산이 시간에 따라 변하지 않는다.
- 시차(lag)에만 의존, 실제 특정 시점 t, s에는 의존하지 않는다.
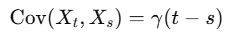
t: 1 2 3 4 5
X: 2, 3, 2, 3, 2
- 자기공분산(1시차, lag=1) = Cov(X_2,X_1), Cov(X_3,X_2), Cov(X_4,X_3), Cov(X_5,X_4)
- 값이 거의 일정 → lag=1 공분산은 시간에 관계없이 일정시계열 분석
일변량 시계열분석
- 변수가 하나일 때 사용하는 시계열 분석 (하루 매출액, 기온 변화)
- 단일 변화 패턴만 고려
- 과거 값으로 미래를 예측 (독립 변수가 없음)
- 추세, 계절성, 주기 분석
다중 시계열분석
- 여러 변수가 시간 흐름에 따라 함께 변할 때, 변수 간 상관관계까지 고려하여 분석
- 매출 예측 (광고비, 방문자 수, 가격 변화)
- 여러 시계열 간의 상호작용을 모델링
- 한 변수의 변화가 다른 변수에 미치는 영향을 분석
이동평균법 (Moving Average)
- 가장 최근 N개의 관측값을 단순 평균하여 다음 값을 예측하는 방법 (예측값 = (3일 전 + 2일 전 + 1일 전) / 3)
- 최근 N개 데이터에 동일한 가중치
- 오래된 데이터(N일 이전)는 완전히 제외
- 계절변동과 불규칙변동을 제거하고 추세변동과 순환변동만 가진 시계열로 변환하는 방법 이용
- 데이터 노이즈 감소에 좋음
- 급격한 변화에는 반응이 느림
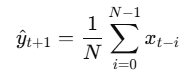
지수평활법 (Exponential Smoothing)
- 이동평균법의 단점을 개선하기 위해 최근 데이터에 더 큰 가중치, 오래된 데이터에 지수적으로 감소하는 가중치를 주는 방법
- 단기간에 발생하는 불규칙변동을 평활 (불규칙변동의 영향을 제거하는 효과)
- 자료 수가 많고 안정된 패턴일수록 예측력이 증가
- α : 평활 상수 (0~1),
- α ↑ → 최근 데이터에 민감하게 반응

AR 모델 (Auto-Regressive Model, 자기회귀 모형)
- 현재값이 과거 자기 자신의 값의 선형결합으로 설명되는 모델 (정상성을 가정)
- 백색잡음의 현재값과 자기자신의 과거값의 가중합으로 선형성을 표현하는 정상 시계열 모형
- AR(p) 모형은 계수 조건(역근조건) 을 만족해야 정상성을 보장
- 모형에 사용하는 시계열 자료의 시점에 따라 1차, 2차, ----, p차 등을 사용하나 정상 시계열 모형에서는 주로 1,2차를 사용
- 과거 값이 현재를 예측한다.
- 시계열 데이터가 자기상관(ACF·PACF) 이 있을 때 적합
- 과거에 관성이 있는 데이터, 즉 추세로 이어지는 패턴을 잘 모델링
- ACF는 빠르게 감소, PACF는 어느 시점에 절단점을 가진다.

→ 현 시점의 자료가 p시점 이전의 과거 자료로 설명될 수 있는 모형
MA 모델 (Moving Average Model, 이동평균모형)
- 현재값이 과거 오차(쇼크, 충격)의 선형결합으로 표현되는 모델
- 정상 시계열을 기반으로 한 모형, MA(q) 모형은 항상 정상 시계열을 만족
- 과거의 충격(오차)이 현재에 영향을 준다.
- 시간이 지날수록 관측치의 평균이 지속적으로 증가, 감소하는 경향을 표현한 시계열
- 현시점의 자료를 유한개의 백색잡음으로 결합 → 항상 정상성 만족
- 특정 시점의 충격이 몇 기간 동안 영향을 미칠 때 유용
- ACF가 특정 lag 이후 절단(cut-off)되는 시계열에 적합
- ACF에서 절단점을 갖고, PACF가 빠르게 감소
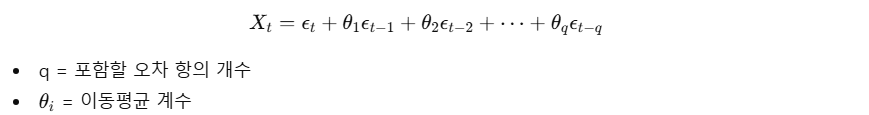
AR(p) = 과거 관측값 사용
MA(q) = 과거 오차를 사용
ARMA 모델 (Autoregressive Moving Average)
- AR(p) + MA(q)의 결합 모델
- 과거 값 + 과거 오차 모두 고려
- 정상성(stationary) 시계열에서만 사용 가능
- AR과 MA의 장점을 모두 사용하여 더 복잡한 패턴을 잡아냄
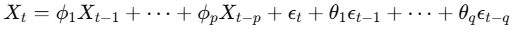
ARIMA(p, d, q) (Autoregressive Integrated Moving Average)
- ARMA 모델을 비정상(non-stationary) 시계열에도 적용할 수 있도록 차분(differencing) 을 도입한 모델
- ARIMA는 비정상 시계열 모형 → 차분, 변환 → AR, MA, ARMA 모형으로 정상화
- p = AR 차수 (과거 값 몇 개를 쓰는지)
- d = 차분(differencing) 횟수 = 추세 제거 정도
- q = MA 차수 (과거 오차를 몇 개 쓰는지)
- d번 차분한 시계열을 Yt라고 하면 (ex. 1차 차분 Yt=Xt - Xt-1)
Yt가 ARMA(p, q) 구조를 가지는 모델이 ARIMA(p,d,q)
d = 0 → ARMA(p, q) 모형, 정상성 만족
p = 0 → IMA(d, q) 모형, d번 차분하면 MA(q)
q = 0 → ARI(p, d) 모형, d번 차분한 시계열이 AR(p) 모형
- ARMA(2,0) = AR(2)
- MA(2) = ARMA(0,2)
ARIMA(p, 0, 0) 모형은 자기회귀 모형 = AR(p)
ARIMA(0, 0, q) 모형은 이동평균 모형 = MA(q)
ACF (Autocorrelation Function, 자기상관함수)
- 시계열 Xt가 k 시점(k lag) 떨어진 과거 값 Xt−k와 얼마나 상관되어 있는지 측정한 것
- 특정 시간 지점 간의 상관관계를 측정하여 시계열 데이터의 패턴과 주기를 파악하는 데 사용
- 전체 자기상관 측정
- 과거 k 시점과 현재 값이 얼마나 유사하게 움직이는가
- AR 모델은 ACF가 천천히 감소
- MA 모델은 ACF가 특정 lag에서 절단(Cut-off)
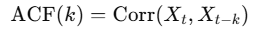
PACF (Partial Autocorrelation Function, 부분자기상관함수)
- PACF는 중간 단계의 영향을 제거한 뒤, 오직 직전 k시점과 현재값의 순수한 상관관계를 측정한 것
- 직접적인 자기상관 측정
- Lag k 시점만 직접적으로 현재값에 영향을 주는 정도
| AR | 과거 값으로 현재를 설명 현재 값 = 과거 값들의 가중합 어제랑 비슷하면 오늘도 비슷할 거야 오늘 기온은 어제 기온의 영향을 강하게 받음 → AR(1) 적합 PACF에서 p차 이후 급격히 0 |
| MA | 과거 오차(충격)로 현재를 설명 현재 값 = 과거 오차들의 가중합 며칠 전 있었던 사건의 여파 뉴스, 정책 발표, 사고, 그때의 충격이 며칠간 영향 ACF에서 q차 이후 급격히 0 |
| ARMA | AR + MA 현재 = 과거 값 + 과거 오차 정상 시계열(stationary) 전제 과거 패턴 + 뉴스 충격 혼합 |
| ARIMA | ARMA + 차분(D) 대부분 현실 데이터는 추세 있음 |
| ACF | 과거와 얼마나 닮았는지 |
| PACF | 직접적인 영향만 측정 |
'개발 > Python' 카테고리의 다른 글
| 텍스트 마이닝 (1) | 2025.12.07 |
|---|---|
| 연관분석 (Association Analysis) (0) | 2025.11.30 |
| 최우추정량 (MLE, Maximum Likelihood Estimator) (0) | 2025.11.26 |
| 지식증류 vs 전이학습 vs 파인튜닝 (0) | 2025.11.26 |
| 통계 기본 (0) | 2025.11.26 |


댓글