공분산 행렬

전체 링크

 

공분산 (Covariance)

- 두 변수 X, Y가 있을 때,

- 둘이 함께 증가하거나 감소 → 양의 공분산

- 한쪽이 증가할 때 다른 쪽이 감소 → 음의 공분산

- 서로 관련 없음 → 0에 가까움

 

공분산 행렬

- 변수가 여러 개일 때(예: X₁, X₂, X₃ …),  각 변수 쌍의 공분산을 모두 모아 만든 정사각 행렬

- 대각선 = 각 변수의 분산

- 비대각 = 변수들 사이의 공분산

- Cov(Xᵢ, Xⱼ) = Cov(Xⱼ, Xᵢ) → 대칭행렬) 

- Positive semi-definite (행렬이 어떤 방향으로도 음수가 되는 제곱 길이를 만들지 않는 성질)

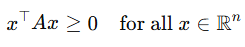
→ 모든 벡터 x에 대해 절대 음수가 되지 않는 성질

 

 

변수 3개에 대한 공분산 행렬

 

PCA

- 공분산이 큰 방향 = 데이터가 가장 퍼져 있는 축

→ 주성분을 찾음

 

LDA

- 클래스별 공분산 행렬이 동일하다고 가정

 

Gaussian Mixture Model

- 각 클러스터마다 다른 공분산 행렬을 가짐 (full, diagonal 등 옵션)

 

다변량 정규분포

- 분산 대신 공분산 행렬로 형태가 결정됨

 

* cov() 함수로 공분산을 계산할 수 있다.

import pandas as pd
import numpy as np

# 예제 데이터 생성
np.random.seed(0)
X = np.random.normal(0, 1, 100)
Y = 2*X + np.random.normal(0, 1, 100)

# 데이터프레임 구성
df = pd.DataFrame({
    'X': X,
    'Y': Y
})

# 공분산 행렬 계산
cov_matrix = df.cov()
cov_matrix

 

공분산 분포 예시

import numpy as np
import matplotlib.pyplot as plt

# Parameters for the grid
n_rows = 10
n_cols = 10
samples = 300
mean = [0, 0]
var_y = 1.0

# Var(X) values (rows): from small to large
var_x_list = np.linspace(0.2, 4.0, n_rows)

# Correlation values (cols): from negative to positive
corr_list = np.linspace(-0.9, 0.9, n_cols)

fig, axes = plt.subplots(n_rows, n_cols, figsize=(10, 10), sharex=False, sharey=False)

for i, var_x in enumerate(var_x_list):
    for j, corr in enumerate(corr_list):
        cov = corr * np.sqrt(var_x * var_y)  # ensures valid covariance
        cov_matrix = [[var_x, cov],
                      [cov, var_y]]
        data = np.random.multivariate_normal(mean, cov_matrix, samples)
        ax = axes[i, j]
        ax.scatter(data[:, 0], data[:, 1], s=8)
        # compact titles to avoid clutter
        ax.set_title(f"VarX={var_x:.2f}\nρ={corr:.2f}", fontsize=7)
        ax.tick_params(axis='both', which='major', labelsize=6)
        ax.set_xlim(-4*np.sqrt(var_x), 4*np.sqrt(var_x))
        ax.set_ylim(-4*np.sqrt(var_y), 4*np.sqrt(var_y))

plt.suptitle("10×10 grid: rows=Var(X) (small→large), cols=Corr(X,Y) (neg→pos)", fontsize=12)
plt.tight_layout(rect=[0, 0, 1, 0.96])
plt.show()