GradientBoosting
- 잔여 오차에 새로운 예측기를 학습 → 모든 학생의 실수 패턴을 분석해서 더 집중해서 가르치기
- 많은 작은 트리(약한 학습기)의 조합으로 강력한 예측 성능을 만듦
- 약한 모델(주로 결정 트리)을 순차적으로 학습해 이전 모델의 오류(gradient)를 보완
- (오류 = 실제 값 - 예측 값)
- 실제 결과를 y, 피쳐를 x1, x2, ..., xn, 피처에 기반한 예측 함수를 F(x)라고 할 때,
- 오류식 h(x) = y - F(x)가 되고 이 식을 최소화하는 방향성을 가지고 반복적으로 가중치 값을 업데이트
- 단계별로 손실 함수를 줄여 나가기 때문에 병렬 처리가 불가능
- 이전 학습기의 잔차(residual)를 새로운 학습기의 목표값으로 사용
- 잔차에 대해 예측하는 모델을 추가하여 앙상블 모델을 구성
- 잔차는 loss function의 negative gradient와 같다. (잔차 = 실제값 - 예측값 : 자체가 gradient)
- 오차를 줄이기 위해 잔차(residual)를 모델링하는 방식을 경사 하강법으로 일반화한 방식 (잔차를 학습)
- 손실 함수로 동작하며 Negative Gradient를 잔차로 사용하여 모델을 학습
- Stochastic Gradient Boosting : 랜덤 샘플링을 적용해 성능 개선과 과적합 방지
장점
- 비선형 관계에 강하고 대부분의 데이터셋에서 높은 정확도를 보임
- XGBoost · LightGBM의 원리 기반
- 다양한 손실 함수 사용 가능
- 과적합 제어 가능
- 노이즈에 상대적으로 덜 민감 (AdaBoost 대비)
- 변수 중요도(feature importance) 제공 (모델 해석 편의)
단점
- 모델을 순차적으로 학습해야 하기 때문에 병렬화가 어렵고 시간이 많이 걸림 (많은 트리 + 작은 learning rate)
- 파라미터를 적절히 설정하지 않으면 쉽게 과적합 → 트리가 깊을수록 과적합 위험
- 하이퍼 파라미터 튜닝이 어려움
하이퍼 파라미터
from sklearn.ensemble import GradientBoostingClassifier, GradientBoostingRegressor
GradientBoostingClassifier(
loss='deviance',
learning_rate=0.1,
n_estimators=100,
subsample=1.0,
criterion='friedman_mse',
min_samples_split=2,
min_samples_leaf=1,
min_weight_fraction_leaf=0.0,
max_depth=3,
min_impurity_decrease=0.0,
min_impurity_split=None,
init=None,
random_state=None,
max_features=None,
verbose=0,
max_leaf_nodes=None,
warm_start=False,
presort='auto',
validation_fraction=0.1,
n_iter_no_change=None,
tol=0.0001,
)
GradientBoostingRegressor(
loss='ls',
learning_rate=0.1,
n_estimators=100,
subsample=1.0,
criterion='friedman_mse',
min_samples_split=2,
min_samples_leaf=1,
min_weight_fraction_leaf=0.0,
max_depth=3,
min_impurity_decrease=0.0,
min_impurity_split=None,
init=None,
random_state=None,
max_features=None,
alpha=0.9, # 회귀
verbose=0,
max_leaf_nodes=None,
warm_start=False,
presort='auto',
validation_fraction=0.1,
n_iter_no_change=None,
tol=0.0001,
)결정 트리와 동일한 하이퍼 파라미터
- criterion : 분할 기준
- splitter : 노드 분할 방법
- max_depth : 트리의 최대 깊이
- min_samples_split : 노드를 분할하기 위한 최소 샘플 수
- min_samples_leaf : 리프 노드에 있어야 하는 최소 샘플 수
- min_weight_fraction_leaf : 리프 노드에 있어야 하는 가중치 샘플의 최소 비율
- max_features : 분할에 사용할 최대 feature 수
- max_leaf_nodes : 최대 리프 노드 수
- min_impurity_decrease : 분할 조건 만족 시 최소 불순물 감소량
그래디언트 부스팅 하이퍼 파라미터
loss
- 최적화할 손실 함수
- 'deviance'는 확률 출력이 가능한 로지스틱 회귀 형태의 손실 함수
- 'exponential'을 선택하면 알고리즘은 AdaBoost와 동일, 노이즈가 적고 단순한 데이터에서 강한 분류 성능
learning_rate
- 모델 학습에서 각 트리(약한 학습기)가 기여하는 정도를 조절
- 새로운 트리가 기존 모델을 얼마나 빠르게 수정할지 결정
- 작은 값 (0.01 ~ 0.1) → 학습이 느리지만, 일반적으로 과적합 감소
- 큰 값 (0.5 ~ 1) → 학습이 빠르지만, 과적합 위험 ↑
- learning_rate를 낮추면 n_estimators를 늘려야 성능 유지 가능 (trade-off)
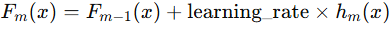
n_estimators
- 부스팅 단계 수(트리 개수)
subsample
- 각 단계에서 사용할 샘플 비율
- 1.0 미만이면 확률적(Stochastic) 부스팅 → 분산 감소 vs 편향 증가 trade-off
validation_fraction
- early stopping (validation 기반) 사용 시 검증 데이터 비율
- 학습 데이터에서 validation_fraction만큼 검증용 데이터로 분리
- 각 boosting 단계에서 검증 데이터의 loss를 계산
- 일정 횟수(n_iter_no_change) 동안 검증 loss가 개선되지 않으면 학습 종료
- 너무 작으면 검증 loss가 안정적이지 않아 조기 종료 실패, 너무 크면 학습 데이터가 줄어 덜 학습
- loss 변화량이 tol보다 작으면 개선 없다고 판단
n_iter_no_change
- early stopping, 지정된 횟수 동안 성능 개선 없으면 중단
tol
- 조기 종료 시 최소 개선 허용값
alpha
- 손실 함수(loss function) 중에서 특정 분포를 정의하는 데 사용되는 계수
- 회귀 모델에만 존재
- 값이 작으면 : 이상치 영향 ↓ → 안정적 학습
- 값이 크면 : 이상치도 반영 → 과대적합 가능 ↑
- 특수 손실 함수 (loss='huber' or 'quantile')에서
비대칭 또는 이상치(outlier)에 강한 회귀를 만들기 위해 데이터의 분포를 특정 분위수(quantile)로 나누어 최적화
분위수(quantile)를 결정하는 값이 alpha (ex. 0.5 → 중앙값 회귀)
quantile loss
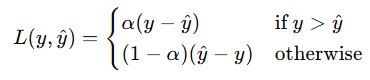
loss='huber'
- Huber 손실은 이상치에 강한 손실이며, alpha는 이상치로 간주할 범위를 결정
- alpha가 작을수록 → 이상치 처리를 더 민감하게 함 (더 많은 값이 이상치로 간주됨)
Attributes
n_estimators_ : int
The number of estimators as selected by early stopping (if
``n_iter_no_change`` is specified). Otherwise it is set to
``n_estimators``.
.. versionadded:: 0.20
feature_importances_ : array, shape (n_features,)
The feature importances (the higher, the more important the feature).
oob_improvement_ : array, shape (n_estimators,)
The improvement in loss (= deviance) on the out-of-bag samples
relative to the previous iteration.
``oob_improvement_[0]`` is the improvement in
loss of the first stage over the ``init`` estimator.
train_score_ : array, shape (n_estimators,)
The i-th score ``train_score_[i]`` is the deviance (= loss) of the
model at iteration ``i`` on the in-bag sample.
If ``subsample == 1`` this is the deviance on the training data.
loss_ : LossFunction
The concrete ``LossFunction`` object.
init_ : estimator
The estimator that provides the initial predictions.
Set via the ``init`` argument or ``loss.init_estimator``.
n_estimators_
- 조기 종료 시 선택된 최종 트리 수
feature_importances_
- 각 피처의 중요도(importance)
- 값이 클수록 해당 피처가 모델 결정에 중요함
oob_improvement_
- OOB(out-of-bag) 샘플 기준 손실 감소량.
train_score_
- 각 반복 단계에서 학습 데이터 손실 값(= deviance).
loss_
- 실제 사용된 손실 함수 객체.
init_
- 초기 예측에 사용된 estimator 객체.
estimators_
- (트리 수 × 클래스 수) 형태로 저장된 개별 트리 모델. 이진 분류면 loss_.K = 1
'개발 > Python' 카테고리의 다른 글
| AdaBoost Hyper Parameters and Attributes (0) | 2025.11.22 |
|---|---|
| 분류 모델 평가 옵션 (F1 Score) (0) | 2025.11.21 |
| K-Nearest Neighbors Hyper Parameters (0) | 2025.11.18 |
| RandomForest Hyper Parameters and Attributes (0) | 2025.11.16 |
| DBSCAN Hyper Parameters and Attributes (0) | 2025.11.15 |

댓글