불편추정량
- 평균적으로 맞는 추정량
- 기댓값이 참값(모평균)인 추정량
- 모분산의 불편추정량 = 기댓값이 모분산과 같다
- 같은 실험(표본추출)을 무한히 반복하면 θ^의 평균이 진짜 값 θ와 같아진다.
- 수학적으로 추정량 가 모수 θ에 대해 불편(unbiased)하다는 것은

를 만족
- 직관적이고 해석이 명확함 → 평균적으로 맞다.
- 통계 이론(예: MVUE, CRLB)에서 깔끔한 성질을 가짐
ㄴ 불편성은 좋은 성질이지만 분산, MSE, 일치성, 효율성 등 다른 기준들과 함께 고려해야 함
- 불편성을 강박적으로 추구하면 분산이 커져 실제 성능(MSE)이 나빠질 수 있음
- 표본이 작을 때는 불편 추정량이 실무적으로 선호되지 않을 수도 있음
편향
- 추정량이 모수에서 평균적으로 얼마나 벗어나는지를 나타내는 지표
- 불편추정량이면 bias = 0
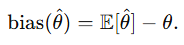
예시
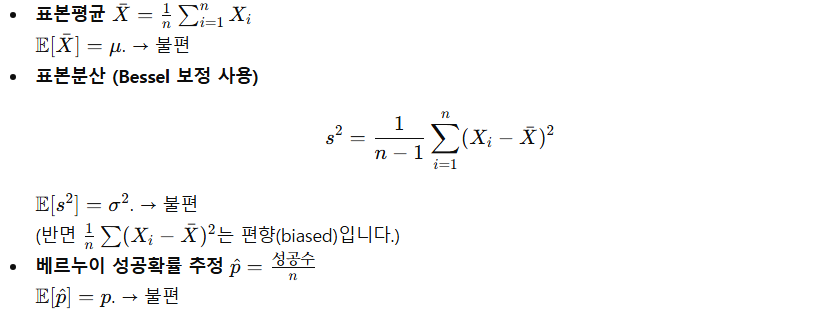
불편성과 다른 성질들의 관계
일치성(consistency)
- 큰 표본에서 확률적으로 수렴.
- 자료의 개수가 무한이면 모평균에 근접하는 추정량
- 표본이 많아질수록 추정값이 진짜 값에 확률적으로 수렴
- 불편성과는 별개 (어떤 추정량은 불편이지만 불일치할 수 있고, 편향이 있어도 일치할 수 있음)

ex.

→ 표본평균은 모평균의 일치 추정량
- 불편 추정량은 표본이 작아도 평균적으로 맞음
- 일치 추정량은 표본이 적으면 실제 값에서 멀 수 있음, 하지만 표본이 커지면 정확해짐
효율성(efficiency)
- 같은 불편추정량들 중 분산이 작은 것이 더 효율적
- Cramér–Rao 하한(CRLB) : 어떤 상황에서는 불편추정량이 이 하한을 만족하면 최적
MVUE (Minimum Variance Unbiased Estimator)
- 모든 불편추정량 가운데 분산이 최소인 추정량(특정 조건 하에 존재)
- Lehmann–Scheffé 정리 사용.
MSE(Mean Squared Error)
- MSE를 기준으로 보면 완전 불편이 꼭 최선은 아님
- 편향을 약간 도입해 분산을 크게 줄이면 MSE가 작아질 수 있음 (ex. Ridge 회귀, 편향-분산 trade-off)
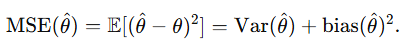
최대가능도추정량 (MLE, Maximum Likelihood Estimation)
- 모평균의 가능도함수를 최대화하는 추정량
최소분산불편추정량(MVUE, Minimum Variance Unbiased Estimator)
- 모평균의 분산을 최소화하는 추정량
예시
실제 온도가 20°C일 때, 특정 온도계가 항상 1°C 높게 나온다면? (21°C, 21.2°C, 20.9°C)
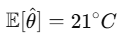
→ 해당 온도계는 biased estimator
과학실험에서 사용되는 고정밀 온도계는 20°C로 측정
→ 평균적으로 맞는 추정량 = 표본의 기댓값이 모수와 같음
→ 여러 번 측정 후 평균이 항상 진짜 목표값을 맞추려고 함 (불편성)
→ unbiased estimator
'개발 > Python' 카테고리의 다른 글
| DBSCAN Hyper Parameters and Attributes (0) | 2025.11.15 |
|---|---|
| Distance Matrix (1) | 2025.11.15 |
| Dictionary (0) | 2025.11.15 |
| shift, rolling (0) | 2025.10.26 |
| melt, stack, unstack (0) | 2025.10.26 |



댓글