Distance Matrix
- 여러 개의 점(관측치, 행) 사이의 거리를 행렬 형태로 표현한 것
- 행렬의 크기는 N x N
- D[i,j] = i번째 점과 j번째 점 사이의 거리
- 대각선 D[i,i]=0 (자기 자신과의 거리)
pdist, cdist, squareform (scipy.spatial.distance)
- pdist는 하나의 점 집합 내 모든 쌍의 거리 계산 → pdist(X)
- cdist는 집합 A의 모든 점과 집합 B의 모든 점 사이의 거리 계산 → cdist(X, Y)
- squareform → 정방 행렬로 변경
pairwise_distances (sklearn.metrics)
- 결과가 바로 정방행렬로 나옴
metric
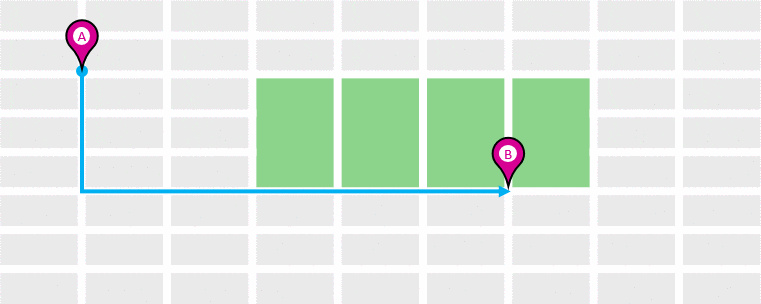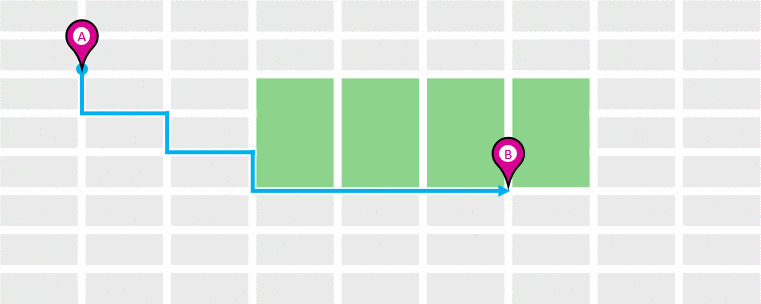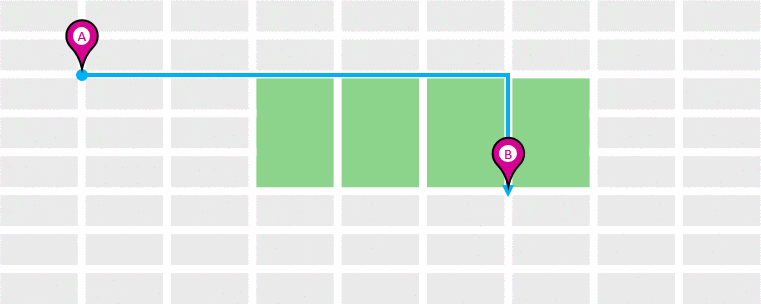
cityblock = manhattan = l1
- 좌표 차이의 절댓값 합
- 특징마다 단순한 절대 차이가 중요한 경우
- 고차원 데이터에 비교적 안정적임
- 장점 : 이상치(outlier)에 유클리드보다 덜 민감
- 단점: 축 방향 이동에만 기반 → 대각선 거리는 덜 반영됨
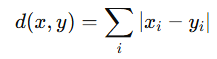
euclidean = l2
- 두 점 사이의 직선 거리
- 기하학적 거리, 군집 분석(k-means 기본 metric)
- 장점: 직관적
- 단점: 고차원에서는 거리 분포가 붕괴됨 (distance concentration)
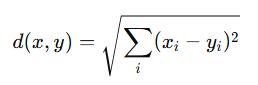
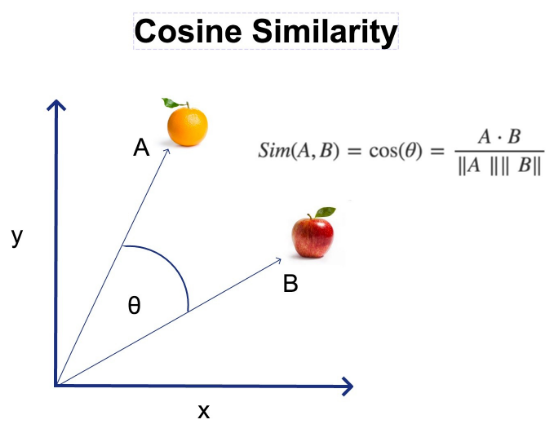
cosine
- 코사인 거리
- 두 벡터의 방향 차이를 측정
- 크기보다는 각도 차이에 의미
- cosine similarity 를 거리로 변환
- 벡터의 크기가 중요하지 않을 때 유용 (텍스트, NLP 문장 임베딩, TF-IDF 등)
- 값이 0에 가까울수록 유사, 1이면 완전 반대 방향
- 장점 : 스케일 차이에 영향 거의 없음
- 단점 : 원점 기준 방향만 보기 때문에 평행 이동에는 부정확

braycurtis
- Bray–Curtis 거리
- 두 벡터의 차이 대비 전체량 비율
- 0~1 범위
- 생태학, abundance 데이터에서 자주 사용
- 크기 차이에 민감하지만 방향 정보는 무시
- 장점 : 비율 기반 비교 가능
- 단점 : 음수 데이터에는 사용 불가
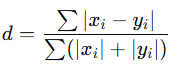
canberra
- 작은 값의 차이를 더 민감하게 반영 (ex. 경제 데이터에서 소규모 차이를 강조할 때)
- 분모가 작으면 거리 기여도가 급격히 증가
- 희소 데이터(sparse)에 적합
- 장점 : 작은 변화에 민감
- 단점 : 0이 포함되면 계산 문제 발생
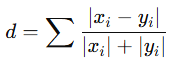
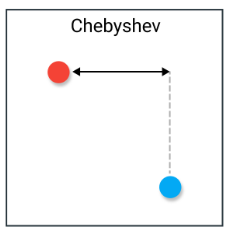
chebyshev
- 체비셰프 거리
- 각 차원별 차이 중 최댓값, 두 벡터 중 가장 큰 차이 (ex. 공정 검증에서 최대 오차값 체크)
- L∞ 노름
- 가장 멀리 떨어진 축 기준 거리
- 장점 : max-error 기반 → 빠르고 단순
- 단점 : 전체 구조는 무시됨
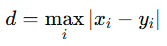
correlation
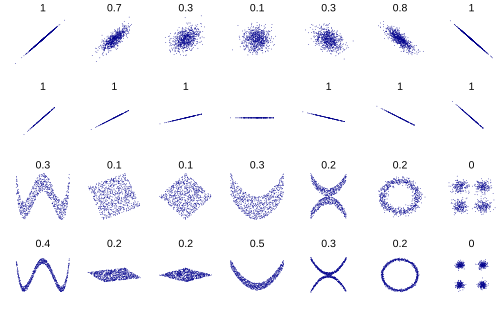
- 상관계수 기반 거리
- 벡터의 크기보다 형태(패턴) 차이가 중요할 때 사용
- 시계열, 패턴 비교, 센서 데이터 유사도에 유용
- 장점 : 평균과 스케일을 제거한 비교
- 단점 : 선형 패턴만 잡아냄

dice
- 이진 벡터에 사용
- Dice similarity 기반 거리
- 텍스트 단어 집합 비교 (set similarity)
- 이미지 분할(segmentation) 마스크 유사도
- 장점 : 교집합을 강조
- 단점 : 음수나 실수 데이터에는 부적합
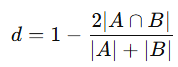
hamming
- 서로 다른 요소의 비율
- 문자열 비교, binary 벡터 비교에서 자주 사용 → 불일치 개수 계산
- n : 요소 개수
- : 조건이 참이면 1, 거짓이면 0을 반환하는 indicator function
- DNA 문자열, 해밍코드 오류 검출
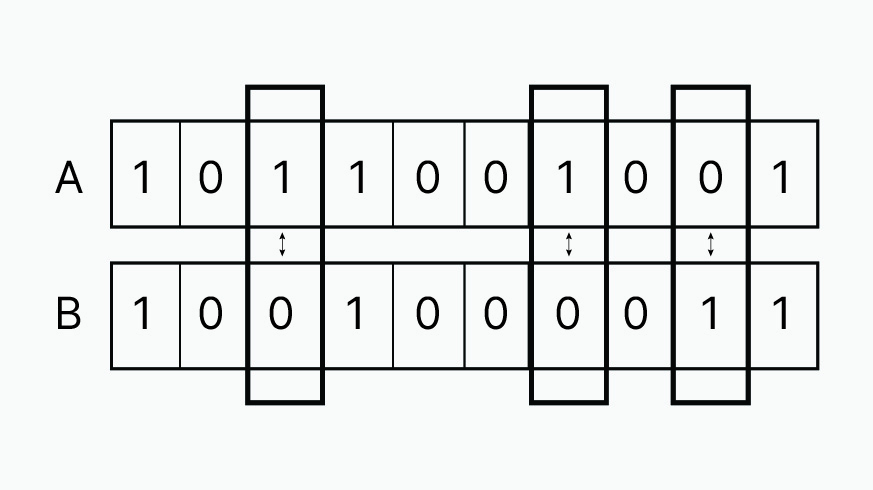
- 서로 다른 위치의 개수 / 전체 길이를 의미
- 장점 : 단순하고 이해하기 쉬움
- 단점 : 숫자 크기 차이는 반영 불가
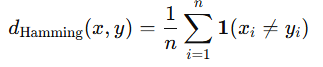
jaccard
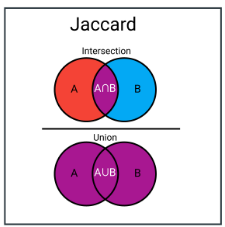
- Jaccard similarity 기반 거리
- 이진 벡터 또는 집합 비교에서 많이 사용 (집합 유사도 비교)
- 키워드 기반 문서 유사도, 추천 시스템에서 취향(좋아요 항목) 비교
- 장점 : 교집합/합집합 기반 명확한 유사도
- 단점 : 다중값(continuous)은 적합하지 않음
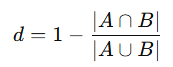
kulsinski
- 이진 데이터용
- Jaccard와 유사하지만 패널티가 다름
- 보수적인 유사도 계산(일치 항목이 적게 반영)
- 드문 경우이지만 이진 벡터 유사도 비교에 사용
- 드문 1(positive event)에 민감
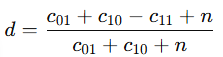
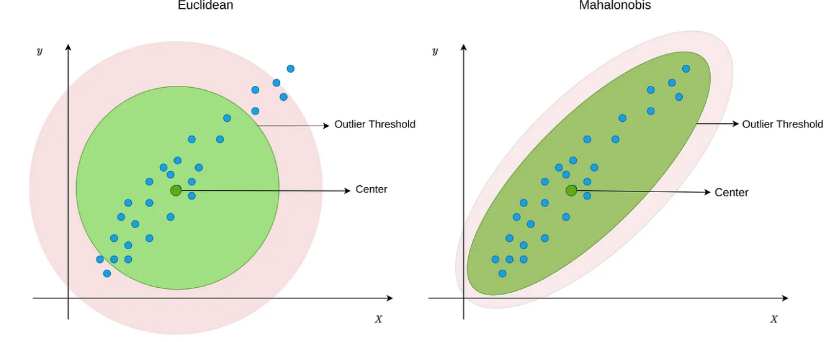
mahalanobis
- 공분산을 고려한 거리
- 서로 상관 있는 특징들에서 매우 중요
- 스케일이 다른 변수들 사이에서 유리
- 이상치 탐지 (대부분 Mahalanobis distance 사용)
- 서로 상관된 변수 있는 데이터 비교
- 장점 : 분포 구조까지 반영
- 단점 : 공분산 행렬이 필요 → 계산 비용 높음
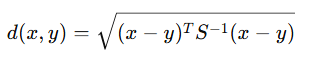
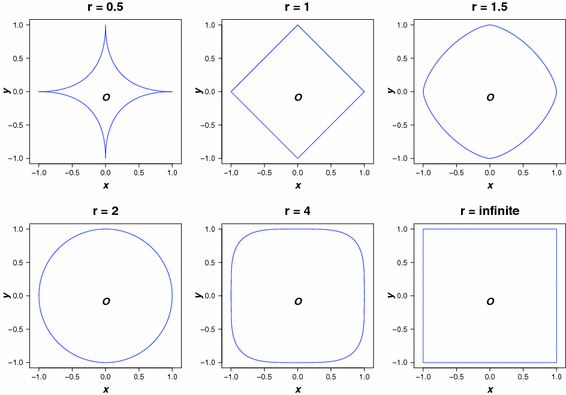
minkowski
- Lp 거리
- p=1 → L1 (Manhattan)
- p=2 → L2 (Euclidean)
- Chebyshev(p→∞)도 포함하는 일반화 거리
- p ↑ → 큰 차이를 더 강하게 강조, p가 커질수록 작은 차이는 무시, 가장 큰 차이가 대표 거리로 취급

- 최대 오차가 중요한 경우 (제품의 여러 측정 값 중 가장 큰 편차가 기준을 넘는지 확인하기)
- 이상치 확인 (특정 차원에서 값이 조금만 커져도 알람을 주고 싶을 때, 센서 모니터링)
- 특정 차원이 중요한 경우 (여러 차원 중 위험 신호를 감지해야 하는 특정 변수가 존재할 때)
- 무작정 p를 높이면 이상치에 취약해지고, 고차원에서 분별력이 약해지고, 해석력이 감소
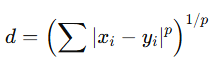
rogerstanimoto
- Rogers–Tanimoto 거리
- binary distance
- 다른 불일치 항목 c01, c10을 2배 가중
- 이진 벡터에서 0과 1의 불일치를 모두 균등하게 보고 싶을 때 사용
- Jaccard, Dice와 달리 0-0 일치도 고려됨
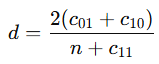
russellrao
- Russell–Rao 거리
- 두 벡터의 공통 1 값 비율 기반
- "둘 다 1인 비율"만 고려하는 특수한 거리 (ex. 두 설문에서 "Yes" 응답비율)
- 장점 : 단순
- 단점 : 0-0 일치는 완전히 무시됨
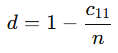
seuclidean
- Standardized Euclidean
- 각 차원을 표준편차로 정규화
- 각 feature의 단위가 다를 때 유용
- 각 변수의 분산을 고려한 거리 필요할 때 사용 (값의 스케일이 크게 다른 데이터)
- 장점 : 스케일 자동 보정
- 단점 : 분산이 0이면 계산 불가
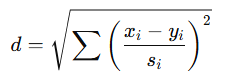
sokalmichener
- Sokal–Michener 거리
- binary data용
- 이진 데이터에서 1-1과 0-0을 동일하게 중요하게 보고 싶을 때 사용
- Rogers–Tanimoto와 유사하나 가중 방식이 다름

sokalsneath
- 이진 거리
- 일치(c11)가 있을 때 거리 감소 (이진 데이터에서 "둘 다 1"인 경우를 매우 중요하게 보고 싶을 때 사용)
- 1의 불일치를 과하게 불이익 줌
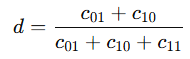
sqeuclidean
- 유클리드 거리의 제곱
- 제곱근이 없어서 계산이 더 빠름
- 기하학적 거리 대신 차이의 제곱 강조 필요
- KMeans에서 내부적으로 사용됨
- 장점 : 계산 효율 좋음
- 단점 : 큰 차이에 매우 민감

yule
- binary data용, odds ratio 기반
- 둘 다 1이거나 둘 다 0인 경우가 매우 중요 (이진 벡터에서 1-1 & 1-0 불일치에 민감하게 반응하는 metric)
- 대칭적이지만 극단적 변화에 민감
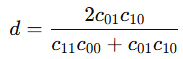
import pandas as pd
import numpy as np
# Try importing scipy
try:
from scipy.spatial import distance
except ImportError as e:
raise ImportError("scipy is not available in this environment.") from e
# Create DataFrame with rows A and B, columns x1,x2,x3
df = pd.DataFrame({
"x1": [1, 4],
"x2": [2, 5],
"x3": [3, 6],
}, index=["A", "B"])
A = df.loc["A"].values
B = df.loc["B"].values
metrics = [
'cityblock', 'cosine', 'euclidean', 'braycurtis', 'canberra', 'chebyshev',
'correlation', 'dice', 'hamming', 'jaccard', 'kulsinski', 'mahalanobis',
'minkowski', 'rogerstanimoto', 'russellrao', 'seuclidean',
'sokalmichener', 'sokalsneath', 'sqeuclidean', 'yule'
]
results = {}
for m in metrics:
try:
if m == "mahalanobis":
VI = np.linalg.inv(np.cov(df.values.T))
d = distance.mahalanobis(A, B, VI)
elif m == "minkowski":
d = distance.minkowski(A, B, 3) # p=3 example
else:
d = distance.cdist([A], [B], metric=m)[0][0]
results[m] = d
except Exception as e:
results[m] = f"ERROR: {e}"
pd.DataFrame.from_dict(results, orient="index", columns=["distance"])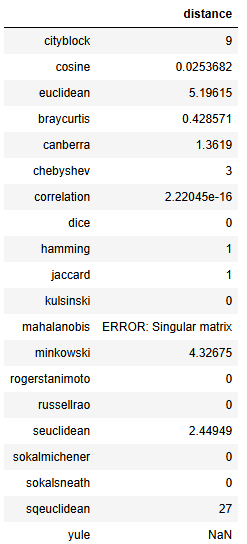
다음 데이터로 Distance Matrix를 만들어 보자
import pandas as pd
import numpy as np
np.random.seed(1234)
data = np.random.randint(0, 2, size=(20, 5))
df = pd.DataFrame(data, columns=['x1', 'x2', 'x3', 'x4', 'x5'])
df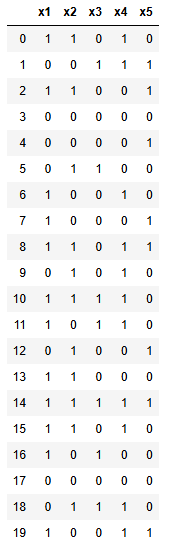
예를 들어 0번째 행과 1번째 행의 manhattan 거리는 다음과 같다.
(df.iloc[0] - df.iloc[1]).abs().sum()
# 0 - 1 1 0 1 0
# 1 - 0 0 1 1 1
# → |1| + |1| + |-1| + |0| + |-1| = 4
pdist를 이용해서 pairwise distance (쌍별 거리)를 계산한다. (manhattan = cityblock)
from scipy.spatial.distance import pdist, squareform
pdist(df.values, metric='cityblock')
이 값을 squareform에 넣으면 정방행렬로 바꿀 수 있다.
from scipy.spatial.distance import pdist, squareform
dist_matrix = squareform(pdist(df.values, metric='cityblock')) # euclidean
dist_df = pd.DataFrame(dist_matrix, columns=[f'row{i}' for i in range(20)],
index=[f'row{i}' for i in range(20)])
dist_df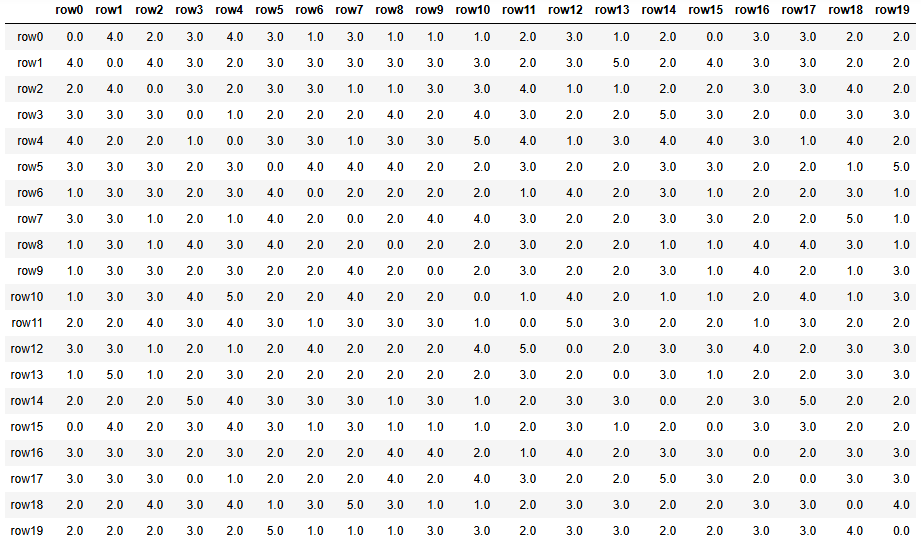
사용자 정의 함수를 이용해서 맨해튼 거리를 계산할 수도 있다.
def my_manhattan(u, v):
return np.sum(np.abs(u - v))
dist_vector = pdist(df.values, metric=my_manhattan)
dist_matrix = squareform(dist_vector)
dist_df = pd.DataFrame(dist_matrix, columns=[f'row{i}' for i in range(20)],
index=[f'row{i}' for i in range(20)])
dist_df자카드 거리
- 두 집합 또는 0/1 벡터가 얼마나 다른지를 측정하는 지표
- 두 집합 A와 B의 자카드 유사도(Jaccard similarity)
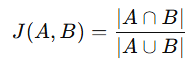
- 자카드 거리(Jaccard distance)

jaccard 옵션으로 쉽게 구할 수 있다.
from scipy.spatial.distance import pdist, squareform
dist_matrix = squareform(pdist(df.values, metric='jaccard'))
dist_df = pd.DataFrame(dist_matrix, columns=[f'row{i}' for i in range(20)],
index=[f'row{i}' for i in range(20)])
dist_df.round(2)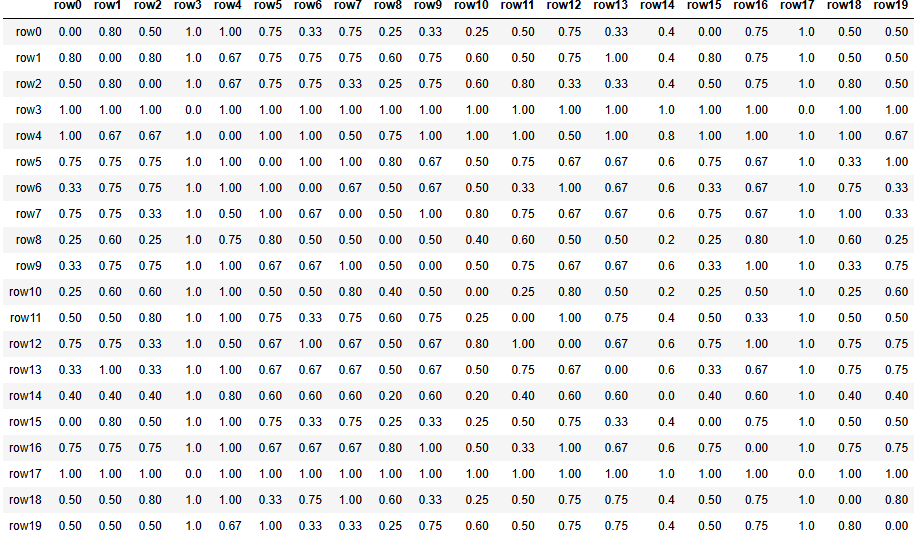
다음과 같이 사용자 정의 함수를 만들어도 같은 결과가 나온다.
def my_jaccard(u, v):
AxB = np.sum(u * v)
A = np.sum(u)
B = np.sum(v)
AUB = A + B - AxB
if AUB == 0: return 0
JAB = AxB / AUB
return 1 - JAB
또는 numpy를 이용해서 다음과 같이 사용자 함수를 만들 수 있다.
def my_jaccard(u, v):
intersection = np.sum(np.logical_and(u, v)) # 교집합
union = np.sum(np.logical_or(u, v)) # 합집합
if union == 0: # 합집합이 0이면 거리 0
return 0.0
return 1 - intersection / union
* pairwise_distances 사용 예시는 다음과 같다.
from sklearn.metrics import pairwise_distances
dist_matrix = pairwise_distances(df.values, metric=my_jaccard)
dist_df = pd.DataFrame(dist_matrix, columns=[f'row{i}' for i in range(20)],
index=[f'row{i}' for i in range(20)])
dist_df.round(2)'개발 > Python' 카테고리의 다른 글
| RandomForest Hyper Parameters and Attributes (0) | 2025.11.16 |
|---|---|
| DBSCAN Hyper Parameters and Attributes (0) | 2025.11.15 |
| 불편추정량 (Unbiased Estimator) (0) | 2025.11.15 |
| Dictionary (0) | 2025.11.15 |
| shift, rolling (0) | 2025.10.26 |




댓글