Ridge : 계수들을 작게(균등하게) 수축(shrink) → 다수의 작은 효과가 있을 때, 다중공선성에 강함.
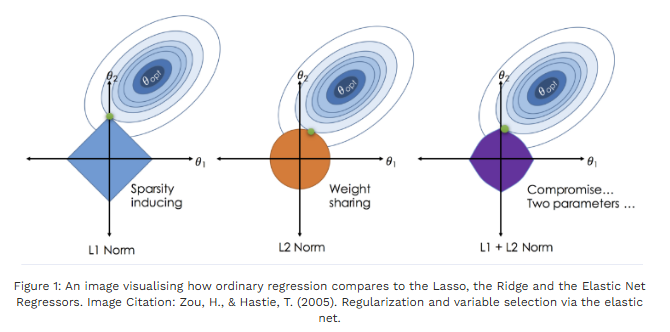
Lasso : 계수들을 제로로 만들며(특징 선택) 희소모델을 만듦 → 해석성 및 변수 선택 목적.
Elastic Net : L1(Lasso) + L2(Ridge) 혼합 → 상관된 변수들 그룹 선택 + 희소성 확보.

- λ가 아주 크면 모든 가중치가 0에 가까워져 수평선 모양(데이터 평균)이 된다. (편향 증가, 분산 감소)
- 학습 종료 후 규제가 없는 지표로 평가한다.
Ridge
- 계수들을 연속적으로(부드럽게) 0 쪽으로 수축.
- 절대값 0이 되는 경우 거의 없음 → 변수 선택을 하지 않음.
- 다중공선성 문제(상관된 컬럼들)에서 분산을 줄여 예측 안정화.
- 해가 닫힌형이라 계산이 빠름(작은 p에서 특히).
- 미분할 경우 2*alpha*W -> 가중치가 작아질수록 감소 속도도 느려져서 천천히 줄어듦
- weight decay 기법
- 변수 간 상관관계가 높은 상황에서 상대적으로 예측 성능이 우수한 것은 릿지(Ridge)
장점
- 다중공선성, 과대적합 완화
- 계산 안정적 (닫힌 해)
- 모형이 매우 불안정하지 않음 (계수 변동 적음)
단점
- 변수 선택을 하지 못해 해석성 떨어짐
- 진짜 희소(진짜 0인 변수)를 찾고자 할 때 부적합
* L2 패널티는 계수를 0으로 만들지 않기 때문에 LARS를 사용하지 않는다.
Lasso
- L1 제약의 기하학적 특성(다이아몬드 형태) 때문에 많은 계수가 정확히 0이 됨 → 변수 선택, 희소 모델
- 해석성 좋음(사용된 변수만 남음)
- 상관된 변수들 중 하나만 선택하는 경향(불안정할 수 있음)
- 최적화는 좌표하강, LARS 등으로 해결 (계수 경로, piecewise linear)
- 미분할 경우, sign(W) 형태로, 항상 일정한 힘을 줌 → W를 강하게 밀어 붙여서 정확히 0으로 만드는 효과
- 0에서 미분이 불가능 해 Gradient-Based Learning 시 주의 필요, L2 대비 효과 감소
- 모델에 Sparsity를 가함
장점
- 자동으로 변수 선택 (모델 단순화, 해석 가능).
- 특정 변수만 중요할 때 성능·해석성 좋음.
단점
- 상관된 변수들에서 임의로 하나만 선택 → 선택 불안정성
- 큰 계수는 편향이 생김 (과도한 수축)
- 해가 존재하지만 닫힌 형식 아님 (계산 복잡도↑, 특히 p 매우 클 때)
* LassoLars
- Lasso 문제를 Least Angle Regression (LARS) 알고리즘으로 해결
- LARS는 계수를 점진적으로 선택하면서 경로를 따라가며 Lasso를 풀 수 있는 효율적 알고리즘
- n ≪ p (샘플 수보다 변수 수가 많을 때) 에 강점
- LassoLars는 Lasso와 결과는 동일하지만 계산 방식이 다름
- 정규화된 데이터를 사용하면 Lasso와 거의 동일한 결과
- 잡음이 많거나 변수 상관이 높으면 결과가 불안정할 수 있음
Elastic Net
- L1의 희소성 + L2의 안정성(그룹 효과) 결합
- 상관된 변수들 그룹을 함께 선택하는 경향 (grouping effect)
- p ≫ n (변수가 샘플수보다 많은) 상황에서 Lasso보다 훨씬 안정적
- Lasso의 상관 변수 선택 불안정성을 L2가 보완 → 안정적인 변수 선택 가능
장점
- 상관변수 그룹을 함께 선택 → 안정성 ↑
- p ≫ n 혹은 변수 그룹화 상황에서 실전에서 자주 더 좋은 성능
단점
- 하이퍼파라미터(λ와 α)를 둘 다 튜닝해야 해서 복잡성 ↑
- 여전히 L1에 의해 일부 편향 발생.
한계점
스케일 의존성
- 모든 방법은 피처 스케일에 민감
- 반드시 각 변수(특히 Lasso/ElasticNet)는 표준화(평균 0, 표준편차 1)를 해야 함.
- 절편(intercept)은 일반적으로 패널티에서 제외.
하이퍼파라미터 선택(λ, α)
- 교차검증(CV)이 표준. λ의 로그 스케일 탐색(logspace) 권장
선택의 일관성(Consistency)
- Lasso는 변수 선택의 일관성을 보장하려면 데이터가 특정 조건 (ex. irrepresentable condition)을 만족해야 함.
- 현실 데이터에서는 불만족하는 경우가 많아 선택 불안정 발생
편향(Bias)
- 모든 규제는 편향을 도입 → 예측 MSE는 (편향^2 + 분산) 균형을 맞추는 것이 목적.
추론(inference)
- 규제된 계수에 대한 표준적 t-검정 등은 잘못된 결과를 냄
- 선택 이후 OLS 재적합, 또는 "debiased lasso"등 특별 기법 사용
그룹 구조
- 그룹 단위 선택이 필요하면 Group Lasso 같은 방법 고려
- 항상 표준화(평균 0, 분산 1)
- intercept는 중심화 / 제외 : y 중심화, X 컬럼 표준화 → 인터셉트는 따로
- 많은 변수(또는 컬럼 간 상관 높음) → Ridge (계수들을 균등하게 수축하여, 상관된 변수들이 함께 선택)
- Elastic Net 권장 상황 : 상관된 변수들이 많거나 p ≫ n이면 Elastic Net이 가장 무난
- 모델 선택 전략 : 일반적으로 ElasticNetCV, LassoCV, RidgeCV로 λ(및 α) CV 튜닝
- 설명력 향상 : Lasso로 변수 선택 후 선택된 변수로 OLS 재적합하면 편향을 줄일 수 있음 (단, 선택 편향 주의)
- 안정성 확인 : 변수 선택이 중요한 경우엔 Stability Selection (부트스트랩 기반) 권장
- 규제는 계수 크기에 영향을 주므로 절대값이 작아진다 = 중요도가 낮다고 해석하되, 비교는 표준화된 계수 기준으로
해석(변수 선택)이 주 목적 → Lasso (또는 Elastic Net)
예측 성능 / 다중공선성 문제 / 많은 작은 신호 → Ridge
변수들이 서로 강하게 상관 → 희소성도 원함 → Elastic Net
p ≫ n (변수 > 샘플) → Elastic Net 권장
'개발 > Python' 카테고리의 다른 글
| 신경망 파라미터 개수 (0) | 2025.10.20 |
|---|---|
| 차트 (0) | 2025.10.14 |
| 스케일링 (0) | 2025.10.11 |
| Seq2Seq, 어텐션, 트랜스포머 (0) | 2025.10.09 |
| PCA vs LDA vs t-SNE (0) | 2025.10.09 |



댓글