차원 축소
- 훈련 알고리즘의 속도 향상
- 데이터 시각화, 중요한 특정 추출
- 메모리 공간 절약
- 알고리즘 성능 감소
- 계산 비용 증가
- 파이프라인 복잡도 증가
- 변환된 데이터를 이해하기 어려움

- PCA : 전체 분산 보존 → 데이터 압축, 노이즈 제거
- LDA : 클래스 분리 최적화 → 분류 성능 향상
- t-SNE : 시각화 최적화 → 비선형 구조 관찰, 글로벌 구조는 왜곡될 수 있음
PCA는 데이터의 분산을 최대화하는 축을 찾는다.
LDA는 클래스 간 분산을 최대화하고 클래스 내 분산을 최소화하는 축을 찾는다.
PCA는 전체 데이터 셋의 공분산 행렬에 대해 고윳값 분해를 수행한다.
LDA는 클래스 내부 공분산 행렬과 클래스 간 공분산 행렬을 사용하여 고윳값 분해를 수행한다.
공분산 행렬

공분산
- 두 변수 간의 변동을 의미하는 분산
- Cov(X, Y) > 0이면 X가 증가할 때, Y도 증가하는 것을 의미 > 0이면 X가 증가할 때, Y도 증가하는 것을 의미
PCA (Principal Component Analysis, 주성분 분석)
- 데이터의 분산(Variance)을 최대한 보존하면서 차원을 축소
- 비지도 학습(Unsupervised) : 레이블 정보를 사용하지 않음
가정
- 선형성(Linearity) : 주요 구조가 선형 결합으로 설명 가능하다.
- 큰 분산 = 중요한 구조 : 분산이 큰 축이 중요한 정보를 담고 있다고 가정.
- 모든 클래스의 공분산 행렬 (Σ)이 동일하다.
- 평균 중심화 : 데이터가 평균 0 중심으로 되어 있어야 함 (보통 preprocessing에서 함)
- 스케일링 : 표준화 필요 (Standardization)
원리
- 공분산 행렬을 계산하고, 고유값(Eigenvalue)과 고유벡터(Eigenvector)를 구함
- 특잇값 분해(SVD)로 훈련세트를 세 개의 행렬 곱 UΣVT로 분해 → V가 주성분 단위 벡터
- 고유값이 큰 순서대로 데이터를 투영 → 분산이 가장 큰 방향으로 데이터 축소
- 원본 데이터셋과 투영된 것 사이의 평균 제곱 거리를 최소화하는 축
- 두 변수가 지닌 정보량(공분산)을 0이 되도록 선형 변환 → 두 변수 간 중복된 정보가 없음

* 상관 행렬 (Correlation matrix) 기반 PCA
- 데이터 스케일 차이가 큰 경우 상관 행렬 (표준화된 공분산 행렬) 사용
- 변수를 Z-score로 표준화한 후,

의 고유값 분해를 수행
특징
- 선형 변환 : 데이터의 선형 관계만 포착
- 차원 축소 후에도 원본 데이터 구조 일부 유지 → 선택한 주성분 수가 많을수록 분산이 증가하는 경향
- 레이블 정보는 사용하지 않음 → 클래스 분리 목적엔 제한적
- 분석 후 모든 축은 직교한다.
- Eigen Value의 크기에 따라 내림차순 정렬한다.
- SVD = O(m * n^2) + O(n^3), randomized = O(m * d^2) + O(d^3)
잘 적용되는 상황
- 특성이 서로 강하게 선형적으로 연관되어 있을 때 (공분산 구조가 명확)
- 분산이 중요한 정보를 담고 있을 때
→ ex. 센서 데이터, 이미지 데이터에서 밝기/색상 분산
- 다중공선성이 큰 경우 → PCA는 공선성을 줄여주는 역할 가능

효과가 떨어지는 상황
- 데이터가 비선형 구조를 가지고 있을 때 → t-SNE, UMAP 등이 적합
- 분산이 크다고 해서 중요한 정보가 아닌 경우 → ex. 이상치가 분산을 키우는 경우
- 클래스 구분이 중요한데 PCA만 쓰는 경우 → 클래스 정보 고려 안 함
장점
- 계산이 비교적 빠르고 직관적
- 데이터 압축 가능
- 노이즈 제거 가능 (저분산 성분 제거)
단점 / 한계
- 비선형 구조, 비선형적 매니폴드(고차원 공간 안에 있는 저차원 구조)를 잘 반영하지 못함
- 클래스 간 구분이 어려운 경우 존재
- 해석이 직관적이지 않을 수 있음 (주성분이 원래 변수와 의미가 다름)
example
import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
from sklearn.datasets import load_iris
from sklearn.preprocessing import StandardScaler
# 1. 데이터 준비 (Iris 데이터셋)
iris = load_iris()
X = iris.data
y = iris.target
# 2. 데이터 스케일링 (PCA 적용 전 추천)
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
# 3. PCA 적용
# n_components=2 : 2차원으로 축소
# whiten=True : 성분 단위 분산 1로 정규화
pca = PCA(n_components=2, whiten=True, svd_solver='auto', random_state=42)
X_pca = pca.fit_transform(X_scaled)
# 4. 결과 확인
print("원본 데이터 차원:", X_scaled.shape)
print("PCA 후 차원:", X_pca.shape)
print("주성분 벡터 (components_):\n", pca.components_)
print("설명된 분산 비율 (explained_variance_ratio_):", pca.explained_variance_ratio_)
print("특이값 (singular_values_):", pca.singular_values_)
print("각 특성 평균 (mean_):", pca.mean_)
# 5. 시각화
plt.figure(figsize=(8,6))
for label in np.unique(y):
plt.scatter(X_pca[y == label, 0], X_pca[y == label, 1], label=iris.target_names[label])
plt.xlabel('Principal Component 1')
plt.ylabel('Principal Component 2')
plt.title('PCA on Iris Dataset (whitened)')
plt.legend()
plt.grid(True)
plt.show()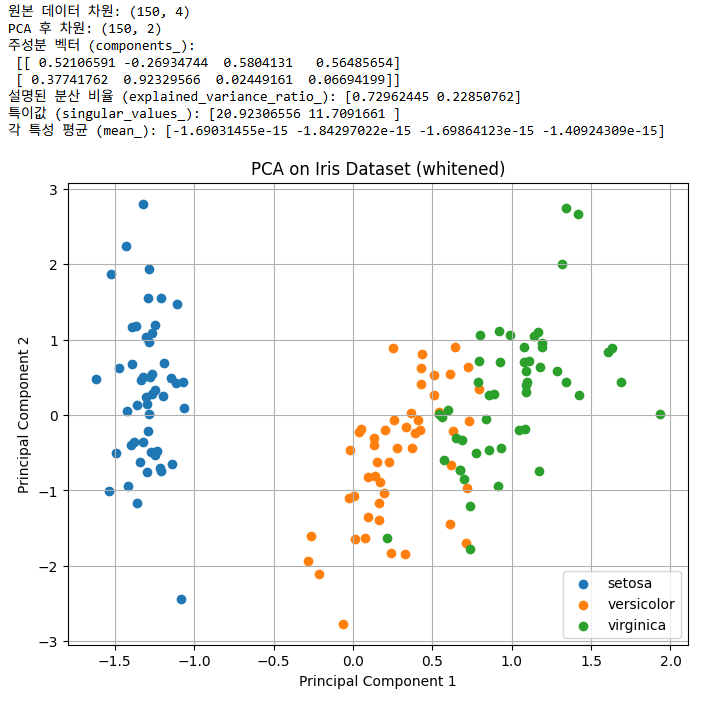
LDA (Linear Discriminant Analysis, 선형 판별 분석)
- 클래스 분리를 최대화하면서 차원 축소
- 지도 학습(Supervised) : 레이블 정보 활용
가정
- 정규성(Normality) : 각 클래스의 데이터가 다변량 정규분포를 따른다.
- 공분산 동일(Homoscedasticity) : 모든 클래스가 동일한 공분산 행렬을 가진다.
- 독립성(Independence) : 샘플들이 서로 독립적이다.
원리
- 클래스 간 분산(Between-class variance)과 클래스 내 분산(Within-class variance)을 계산
- 클래스 간 분산 행렬과 클래스 내 분산 행렬의 비율을 최대화하는 방식으로 선형 판별 축을 찾는다.
- 클래스 간 분산을 최대화하고 클래스 내 분산을 최소화하는 축으로 데이터 투영
- 클래스 내부 공분산 행렬 SW, 클래스 간 공분산 행렬 SB → SW-1 * SB 의 고유값을 분해하여 분리도가 큰 축을 선택
- 클래스 간 공분산 행렬을 구할 때, 각 클래스 평균 벡터와 전체 평균 벡터 간의 차이를 사용한다.

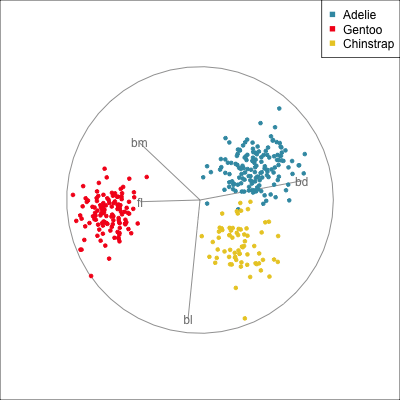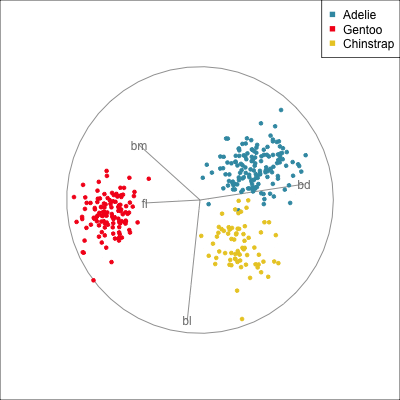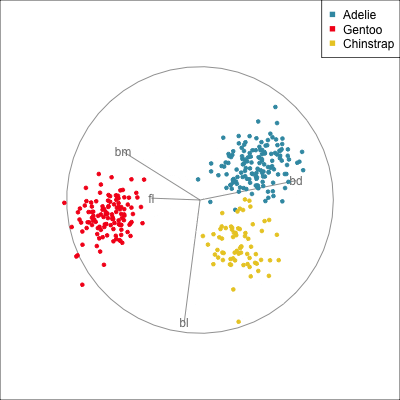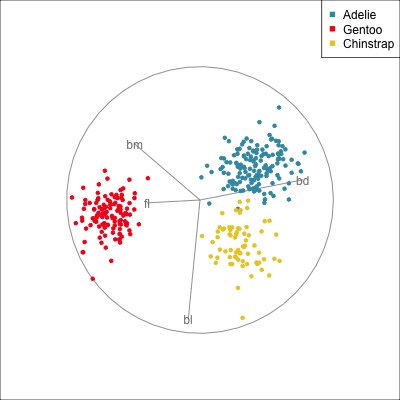
특징
- 선형 변환
- 분류 목적에 최적화
- 레이블 정보 필요
- 각 클래스에 대해 다변량 정규분포를 가지는 것을 가정
- 데이터가 투영되는 초평면을 정의하는 데 사용
- 다른 분류 알고리즘을 적용하기 전에 차원을 축소시킬 때 적합
- 상관관계가 클수록 클래스 간 평균 차이가 커지고 (SB 증가), 클래스 내 분산은 작게 (SW 감소) 된다.
- 축의 수는 최대 C−1 (C = 클래스 수)
잘 적용되는 상황
- 클래스별 평균 차이가 크고, 공분산이 비슷한 경우
→ 클래스 간 분리가 선형적으로 가능하면 LDA가 강력함.
- 클래스 레이블이 존재하고, 클래스 간 선형 경계가 유효할 때
- 다중공선성(Multicollinearity)이 크지 않은 경우
→ 공분산 행렬의 역행렬 계산이 필요하기 때문에 다중공선성이 심하면 불안정.
- 독립변수(X)와 종속변수(y) 사이에 상관관계가 있어야 잘 작동
- 상관관계가 클수록 클래스 간 평균 차이가 커지고 (SB 증가), 클래스 내 분산은 작게 (SW 감소) 된다.
효과가 떨어지는 상황
- 클래스별 공분산이 매우 다를 때 (Heteroscedastic) → Quadratic Discriminant Analysis(QDA)가 적합
- 공분산 행렬이 가역적(정칙)이라는 전제가 있으며, 다중공선성(특성 간 상관성)이 높으면 성능 저하가 발생
ㄴ 다중공선성(변수 간 높은 상관)이 있으면 행렬이 singular (역행렬 불가) 상태가 되어 계산이 불안정
- 클래스 간 평균이 거의 겹치거나 선형으로 분리할 수 없는 경우
- 샘플 수가 적고 특성 수가 많아서 공분산 행렬 추정이 불안정한 경우
- 데이터가 정규분포 가정을 따르지 않는 경우
- 데이터가 비선형 구조를 가질 때



장점
- 클래스 분리 용이
- 차원 축소 + 분류 성능 향상 가능
- 소규모 데이터에도 잘 동작
- 투영을 통해 가능한 한 클래스를 멀리 떨어지게 유지
단점 / 한계
- 선형 경계 가정 → 비선형 분리 데이터엔 성능 제한
- 클래스 수보다 축 수가 제한됨 (C - 1)
- 이상치에 민감
example
# 필요한 라이브러리 불러오기
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.metrics import accuracy_score
# 1. 데이터 불러오기
iris = load_iris()
X = iris.data
y = iris.target
print("Original feature shape:", X.shape)
# 2. 데이터 나누기 (train/test)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42, stratify=y)
# 3. 표준화
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)
# 4. LDA 모델 생성
lda = LinearDiscriminantAnalysis(n_components=2) # 2차원으로 축소
X_train_lda = lda.fit_transform(X_train_scaled, y_train)
X_test_lda = lda.transform(X_test_scaled)
print("LDA transformed feature shape:", X_train_lda.shape)
# 5. LDA로 분류
y_pred = lda.predict(X_test_scaled)
accuracy = accuracy_score(y_test, y_pred)
print("Test set accuracy:", accuracy)
# 6. 2D 시각화
plt.figure(figsize=(8,6))
for class_value, color, label in zip([0,1,2], ['red','green','blue'], iris.target_names):
plt.scatter(X_train_lda[y_train==class_value, 0],
X_train_lda[y_train==class_value, 1],
label=label,
alpha=0.7,
edgecolors='k')
plt.xlabel('LD1')
plt.ylabel('LD2')
plt.title('LDA of Iris Dataset')
plt.legend()
plt.grid(True)
plt.show()
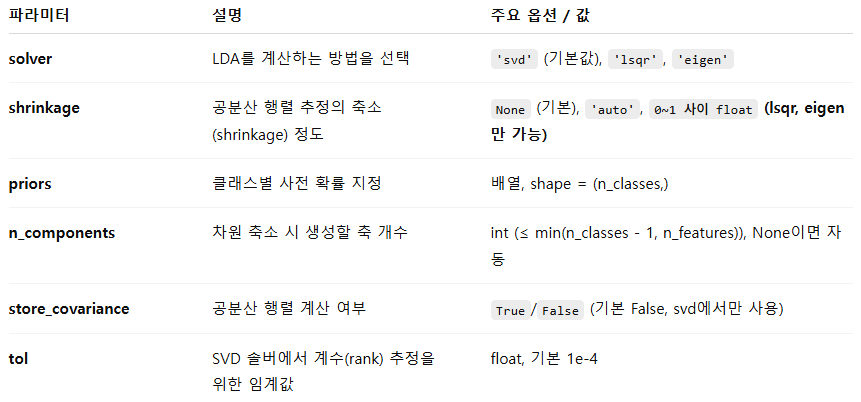

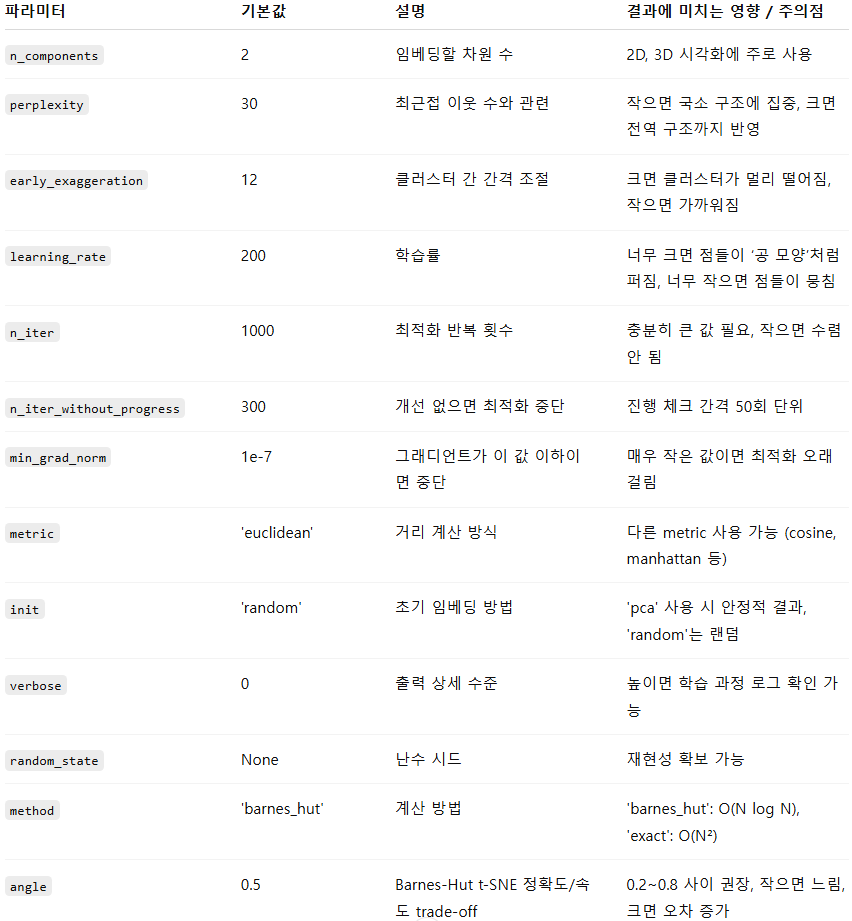
t-SNE (t-distributed Stochastic Neighbor Embedding)
- 확률적 이웃 임베딩
- 고차원 데이터를 2차원 또는 3차원으로 시각화할 수 있도록 차원 축소, 구조 보존하는 "비선형" 기법
- 고차원 공간에서 가까운 데이터들이 저차원에서도 가깝게 유지되도록 설계된 알고리즘 (유사성을 계산)
- 비지도 학습이지만 레이블이 있으면 시각화에 활용 가능
가정
- 로컬 유사성 유지 : 가까운 데이터 포인트들은 저차원에서도 가까워야 한다.
- 거리 기반 의미 : 고차원 공간의 거리 또는 유사성이 저차원에서도 의미가 있음.
원리
- 고차원에서 가까운 점들의 거리 정보를 확률로 변환
- 저차원에서 비슷한 확률 분포를 유지하도록 최적화
- 저차원 투영시 Student t-분포를 사용하여 점 간 거리를 모델링하고, 클러스터 간 겹침을 줄인다.
ㄴ 멀리 떨어진 점들 간의 거리 차이를 크게 만듦
- KL divergence를 최소화(= 손실 함수)하는 방식으로 데이터 위치 결정
- 비선형 차원 축소
- 비슷한 샘플은 가까이, 비슷하지 않은 샘플은 멀리 떨어지게 하면서 차원을 축소
- 데이터 포인트 사이의 유사도를 구하여 확률 분포로 나타내고, 확률 분포가 유사한 방향으로 차원 축소
- 점들의 유사도는 A를 중심으로 한 정규 분포에서 확률 밀도에 비례
- 이웃을 선택할 때 포인트 A가 포인트 B를 이웃으로 선택한다는 조건부 확률 계산
- 저차원 공간에서 데이터를 표현하기 위해 고차원 및 저차원 공간에서 조건부 확률(유사성)간의 차이를 최소화
- 가까운 포인트일수록 높은 확률을 가지도록 가우시안 커널 사용.

특징
- 비선형 : 복잡한 구조까지 시각화 가능
- 지역적 구조(Local structure) 유지에 강점
- 글로벌 구조(Global structure)는 왜곡될 수 있음
- 파라미터에 민감 (perplexity, learning rate)
- 고차원 데이터가 실제로 더 낮은 차원의 다양체(manifold) 위에 놓여 있을 가능성이 있다고 가정하고 저차원으로 투영
- Isomap / UMAP처럼 manifold 보존을 직접 가정하지 않고, 결과가 manifold 위에 놓인 것처럼 보이게 된다.
- 고차원(가우시안 분포), 저차원(Student-t 분포)로 멀리 떨어진 점 간 거리 표현을 강화
잘 적용되는 상황
- 고차원 데이터의 국소적 구조(유사한 샘플 그룹)를 시각화하고 싶을 때
- 비선형 구조를 가진 데이터 → PCA로는 구분이 어려운 패턴도 t-SNE로 그룹화 가능
- 클래스 간 구분보다는 근접 데이터 관계가 중요할 때
효과가 떨어지는 상황
- 전역 구조(global distance)가 중요한 경우 → ex. 전체 데이터 간 상대적 거리
- 샘플 수가 매우 큰 경우 → 계산량 많고 시각화 해석 어려움
- 과도하게 고차원 데이터를 축소하면 혼합된 클러스터 발생 가능
장점
- 시각화에 최적화 → 클러스터 구조 관찰 가능
- 비선형 구조까지 표현 가능
- 직관적이고 이해하기 쉬움
단점 / 한계
- 차원 축소 후 다른 ML 모델 입력으로 사용하기 어려움
- 계산량이 많음, 느린 속도 (→ 대용량 데이터에는 UMAP, PCA + t-SNE)
- 결과가 매번 다를 수 있음 (랜덤 초기화 영향)
- 글로벌 구조 왜곡 가능
- 목적함수가 전체 데이터에만 정의되기 때문에 새로운 데이터가 추가되면 기존 결과에 영향을 미친다.
- 새로운 데이터를 기존 시각화에 바로 넣기 어려움 (비유사한 임베딩)
Kullback-Leibler Divergence
- 한 확률 분포가 두 번째 예상 확률 분포와 어떻게 다른지 측정하는 지표
- gradient descent 방식을 사용하여 전체 데이터 포인트의 KL Divergence 합계를 최소화
- 고차원에서 계산한 유사도와 저차원에서 계산한 유사도의 차이를 KL Divergence로 측정.
- 이 값을 최소화하도록 저차원 임베딩을 반복적으로 업데이트
- 최소화하기 위해 경사하강법을 사용
example
# 라이브러리 불러오기
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.manifold import TSNE
from sklearn.preprocessing import StandardScaler
# 데이터 준비 (Iris 데이터셋)
iris = load_iris()
X = iris.data
y = iris.target
# 표준화 (선택 사항)
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
# t-SNE 적용
tsne = TSNE(n_components=2, perplexity=30, learning_rate=200, random_state=42)
X_tsne = tsne.fit_transform(X_scaled)
# 시각화
plt.figure(figsize=(8,6))
for label in np.unique(y):
plt.scatter(X_tsne[y==label, 0], X_tsne[y==label, 1], label=iris.target_names[label])
plt.legend()
plt.title("t-SNE visualization of Iris dataset")
plt.xlabel("t-SNE 1")
plt.ylabel("t-SNE 2")
plt.show()

그 외
지역 선형 임베딩 (LLE, Locally Linear Embedding)
- 비선형 차원 축소
- PCA와 달리 투영에 의존하지 않음.
- 샘플이 최근접 이웃에 얼마나 선형적으로 연관되어 있는지 측정
- k개의 최근접 이웃을 찾아서 선형 함수로 재구성

다차원 척도법 (MDS, Multidimensional Scaling)
- 샘플 간의 거리를 보존하면서 차원을 축소, 근접성을 시각화하는 통계기법
- 샘플 사이의 유사성, 비유사성을 측정하여 2차원 공간상에 점으로 표현
- 원래 데이터의 거리 정보와 유지, 데이터 간의 유사성을 보존하는 방향으로 축소
- 고차원 데이터의 거리 행렬을 기반으로 저차원에서도 동일한 거리 구조를 유지하도록 최적화
- 고전적(Classical) MDS는 선형 방법
- 비선형 MDS는 Isomap, t-SNE 같은 종류로 확장된 방식

S-STRESS
- 오차 측도 (error measure)
- 대상 간의 유사도/비유사도 정보를 저차원 공간에 배치할 때 원래 거리 정보를 얼마나 잘 보존하는지를 평가
- 값이 0에 가까울수록 좋으며, 0.2 이상은 모형으로 부적합
- MDS는 Stress 함수를 최소화하는 저차원의 값을 찾는다.

example
import numpy as np
import matplotlib.pyplot as plt
from sklearn.manifold import MDS
from sklearn.datasets import load_iris
# 1. 예제 데이터 불러오기 (Iris 데이터)
iris = load_iris()
X = iris.data
y = iris.target
target_names = iris.target_names
# 2. MDS 모델 생성
mds = MDS(n_components=2, # 축소할 차원 수
metric=True, # 거리(metric) 기반 MDS 사용
random_state=42)
# 3. 데이터 변환
X_mds = mds.fit_transform(X)
# 4. 결과 시각화
plt.figure(figsize=(8,6))
colors = ['red', 'green', 'blue']
for i, target_name in enumerate(target_names):
plt.scatter(X_mds[y == i, 0], X_mds[y == i, 1], label=target_name, color=colors[i])
plt.title('MDS on Iris dataset')
plt.xlabel('MDS1')
plt.ylabel('MDS2')
plt.legend()
plt.show()



특이값 분해 (SVD, Singular Value Decomposition)
- M = UΣV.T
- U, V = 특이벡터 (singular vector), 모든 특이벡터는 직교
- Σ = 대각행렬, 대각에 위치한 값만 0이 아니고 나머지 위치의 값은 모두 0이다.
ㄴ 특이값은 M의 크기에 따라 개수가 결정되며, 음수가 될 수 없다. (0 이상의 값)

- PCA는 정방행렬만 가능하지만, SVD는 행과 열의 크기가 다른 행렬에도 적용가능
- m x n = (m x m) @ (m x n) @ (n x n) 으로 분해
- 데이터를 한 방향으로 회전 → 크기를 축마다 늘이거나 줄임 → 다시 다른 방향으로 회전으로 행렬 변환을 완전히 분해

* TruncatedSVD
- SVD는 모든 특이값과 특이벡터를 계산하지만, TSVD는 상위 k개의 특이값/특이벡터만 계산
- 큰 행렬을 저차원으로 압축하거나 근사할 때 사용되는 SVD의 축약 버전
- 희소 행렬에서 계산 효율이 좋음
- 완전 복원 불가능
example
from sklearn.decomposition import TruncatedSVD
# 예시 데이터
X = np.array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
# 2차원으로 축소
svd = TruncatedSVD(n_components=2)
X_reduced = svd.fit_transform(X)
print("차원 축소된 행렬:")
print(X_reduced)
print("설명된 분산 비율:")
print(svd.explained_variance_ratio_)


Compact SVD (Reduced SVD)
- 특히 희소(sparse)하거나 큰 행렬을 다룰 때 효율적인 SVD 방법
- 손실이 발생하지 않은 수준까지 rank를 줄임


'개발 > Python' 카테고리의 다른 글
| 스케일링 (0) | 2025.10.11 |
|---|---|
| Seq2Seq, 어텐션, 트랜스포머 (0) | 2025.10.09 |
| 오즈와 오즈비 (0) | 2025.10.09 |
| 순환신경망 RNN (0) | 2025.10.09 |
| 불균형 데이터 처리 (0) | 2025.10.08 |


댓글