
StandardScaler
- 평균(Mean)을 0, 표준편차(Standard Deviation)를 1로 맞춤. (z-score normalization)
- 데이터가 정규분포(가우시안 분포)에 가까울 때 효과적.
- 평균과 분산이 다른 피처들을 같은 스케일로 맞춰줌.
- 이상치(Outlier)에 민감 → 이상치가 크면 표준편차가 커져서 다른 데이터가 상대적으로 작아짐.

μ : 변수의 평균
σ : 변수의 표준편차
장점
- 많은 모델(선형 회귀, 로지스틱 회귀, SVM, PCA, K-Means 등)에서 기본적으로 잘 작동.
- 확률 해석이나 거리 기반 모델에서 안정적.
단점
- 이상치가 있으면 평균과 표준편차가 왜곡됨.
- 데이터가 정규분포가 아닐 경우 최적 효과가 아닐 수 있음.
적합한 상황
- 정규분포 형태 데이터 (예: 시험 점수, 센서 측정치)
- 선형 모델 (Linear Regression, Logistic Regression)
- 거리 기반 모델 (SVM, KNN, PCA)

MinMaxScaler
- 최소값을 0, 최대값을 1로 변환. (혹은 지정한 범위 [a, b])
- 모든 값이 0~1 구간에 들어감.
- 데이터 분포의 형태를 그대로 유지하면서 크기만 축소.

장점
- 범위가 고정되어 있어서 신경망(딥러닝)에서 학습 안정화에 좋음.
- 분포 모양 자체는 유지
단점
- 이상치에 매우 민감 → outlier 하나 때문에 범위가 크게 늘어나면 대부분 데이터가 0 근처로 몰림
- 실제 최소값/최대값에 따라 결과가 크게 변함.
적합한 상황
- 신경망(Deep Learning) : 시그모이드, ReLU, tanh 같은 비선형 활성화 함수는 입력이 0~1 또는 -1~1일 때 수렴이 빨라짐.
- 정규화된 입력이 중요한 경우 (예: 이미지 픽셀 0~255 → 0~1).
RobustScaler
- 중앙값(Median)을 0, IQR(사분위 범위: Q3 - Q1)으로 나눔.
- 중앙값 기준으로 스케일링 → 이상치(Outlier)의 영향을 거의 안 받음.
- 데이터 분포가 치우쳐 있거나 이상치가 많은 경우 적합.
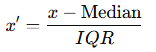
장점
- 이상치에 강함.
- 데이터가 치우쳐 있어도 안정적인 스케일링 가능.
단점
- IQR 기반이므로 분포가 정규분포일 때는 StandardScaler보다 손해.
- 데이터가 모두 균일할 경우 변별력이 줄어듦.
적합한 상황
- 이상치 많은 데이터 (예: 금융 거래 데이터, 로그 스케일의 소득 분포)
- 편향된(Heavy-tailed) 분포
DecimalScaler
- 단순히 숫자의 자릿수를 이동시키는 방식
- 데이터를 0 ~ 1 정도의 범위로 쉽게 압축

장점
- 단순 계산
- 큰 수 데이터를 작은 범위로 쉽게 변환
단점
- 데이터 분포에 따라 적절한 j 값 선택 필요
- 이상치에 민감
적합한 상황
- 단순 정규화가 필요할 때
- 계산 효율을 우선시할 때
'개발 > Python' 카테고리의 다른 글
| 차트 (0) | 2025.10.14 |
|---|---|
| Ridge, Lasso, Elastic Net (2) | 2025.10.11 |
| Seq2Seq, 어텐션, 트랜스포머 (0) | 2025.10.09 |
| PCA vs LDA vs t-SNE (0) | 2025.10.09 |
| 오즈와 오즈비 (0) | 2025.10.09 |



댓글