활성화 함수
- 인공신경망에서 뉴런이 출력값을 어떻게 변환할지 결정하는 함수
- 뉴런의 출력 형태를 결정하고 비선형성 부여
- 복잡한 패턴 학습을 가능하게 함
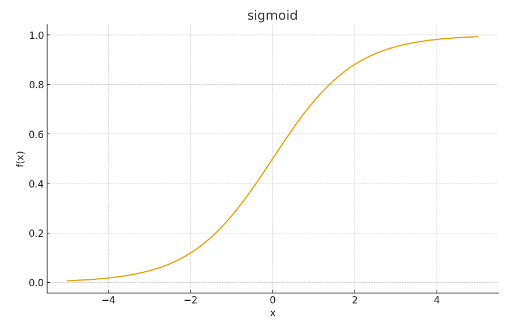
Sigmoid
- 이진 분류의 출력을 0과 1로 정규화 (ex. 스팸메일 분류)
- 현재는 은닉층에서는 거의 사용되지 않음
- 출력층(확률값)에서만 쓰임

장점
- 출력이 확률 해석에 적합
- 초창기 뉴럴넷에서 많이 사용됨
단점
- 기울기 소실(vanishing gradient) → 깊은 신경망 학습 어려움
- 출력이 0 또는 1 근처에서 gradient가 거의 0
- 0을 기준으로 대칭되지 않음 → 학습 비효율, 느린 수렴
Tanh
- 은닉층에서 sigmoid 대체
- 신경망에서 자주 사용
- 출력 범위: -1 ~ 1
- sigmoid의 개선판 (입력이 0 근처일 때 gradient가 더 큼)

장점
- 출력이 0 중심 → sigmoid보다 학습 잘 됨
- 값 변환이 더 자연스럽게 퍼짐
단점
- 여전히 기울기 소실 문제 존재
- 입력이 크면 gradient 0 근처

ReLU (Rectified Linear Unit)
- CNN, DNN 등 딥러닝 전반의 은닉층 기본값
- 대부분 신경망에서 기본 활성화 함수로 사용
- 단순, 효율적 → 현대 기본 활성화 함수

장점
- 계산 빠름 (양수 구간에서 기울기 1로 일정 → 단순)
- 기울기 소실 감소
- Sparse activation → 일부 뉴런만 활성화
- 훈련이 깊은 네트워크에서 매우 잘 작동하는 경험적 성능 입증
단점
- dying ReLU 문제(dead neurons)
→ 음수 입력이면 gradient가 0, 다시 활성화 안 됨

Leaky ReLU
- ReLU의 단점 보완
- CNN, GAN 등에서 사용
- ReLU보다 안정적인 대안

장점
- dead ReLU 완화
- 음수 영역에서도 작은 gradient 유지
단점
- 기울기 계수(0.01)는 임의값 → 항상 최적은 아님 (데이터에 맞지 않을 경우 성능 저하)
- 약간의 비대칭성

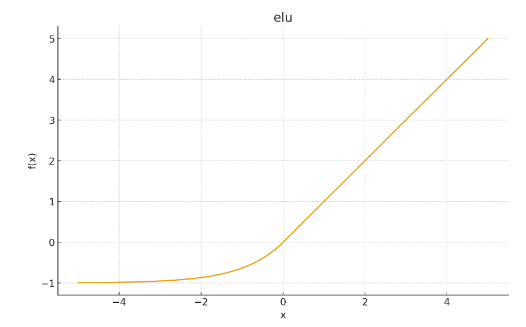
ELU
- 심층 신경망에서 사용
- 학습 안정성 필요한 경우
- Leaky ReLU와 비슷한 목적 + smooth한 형태
- 음수 영역 출력이 음수이므로 mean activation이 0 근처 → 내부 공변량 변화 감소 도움
* 내부 공변량 변화 (internal covariate shift) : 신경망 학습 과정에서 각 층의 입력 데이터 분포가 계속 바뀌는 현상

장점
- 0 중심화 효과
- 음수 구간에서도 gradient 존재
- 평균 활성값이 0 근처 → 학습 유리, 학습 안정화, 경사 하강법 수렴 속도 개선
단점
- ReLU 대비 계산 비용 높음
하이퍼파라미터 최적화 필요

import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-5, 5, 400)
functions = {
'sigmoid': 1 / (1 + np.exp(-x)),
'tanh': np.tanh(x),
'relu': np.maximum(0, x),
'leaky relu': np.where(x > 0, x, 0.01 * x),
'elu': np.where(x > 0, x, 1.0 * (np.exp(x) - 1))
}
for name, y in functions.items():
plt.figure()
plt.plot(x, y)
plt.title(name)
plt.xlabel('x')
plt.ylabel('f(x)')
plt.grid(True)
plt.show()'개발 > Python' 카테고리의 다른 글
| 주요 합성곱 신경망 (0) | 2025.10.06 |
|---|---|
| 경사 하강법, 옵티마이저 (0) | 2025.10.06 |
| 집합 연산 (0) | 2025.10.05 |
| groupby + agg로 여러 컬럼 집계하기 (0) | 2025.10.05 |
| 앙상블 (Ensemble) (0) | 2025.09.14 |


댓글