from xgboost import XGBClassifier, XGBRegressor
from sklearn.ensemble import RandomForestClassifier, RandomForestRegressor
from sklearn.ensemble import AdaBoostClassifier, AdaBoostRegressor
from sklearn.ensemble import GradientBoostingClassifier, GradientBoostingRegressor
from sklearn.neighbors import KNeighborsClassifier, KNeighborsRegressor
from sklearn.ensemble import BaggingClassifier, VotingClassifier
from sklearn.model_selection import GridSearchCV, RandomizedSearchCV
앙상블
- 모든 분류기가 완벽하게 독립 + 오차에 상관관계가 없을 때 가장 성능이 좋다.
→ 다양한 분류기로 학습하면 서로 다른 종류의 오차를 만들어서 성능이 상승
→ 트리 기반의 앙상블은 하이퍼 파라미터가 너무 많아 튜닝에 시간이 많이 소모 (예측 성능이 잘 향상되지도 않음)
배깅
- 훈련 세트의 중복을 허용한 샘플링
- 단일 모델로 동작할 수 있으나 일반화 성능이 떨어짐
- Bootstrap은 Aggregation할 모델들의 다양성을 보이게 함
- 불안정한 결과를 보이는 모델의 분산을 줄여 일반화 성능을 높임
- Aggregation 모델의 수가 늘어나면 분산이 줄어들어 과적합 현상을 완화
- Aggregation = 여러 모델 예측값을 합치는 것
부스팅
- 약한 학습기를 여러 개 결합
- 부스팅 모델을 구성하는 모델의 수를 늘리면 편향은 감소하고, 분산이 커질 수 있다. (과적합)
- 부스팅은 순차적으로 모델을 결합, 병렬화가 어려움
- 틀린 것에 가중치를 주는 방식
- 각 예측기가 선형 분류기였으면 결합된 최종 모델도 선형일 수 있다. (트리인 경우, 최종 모델은 비선형)
- 중간에 weak learner를 써도 마지막에 비선형 결과가 나올 수 있다.
- 학습 데이터에 과적합 될 가능성이 높다.

AdaBoost
- 샘플의 가중치를 수정 → 문제를 많이 틀린 학생에게 더 집중해서 가르치기
- 다음 라운드의 모델을 학습할 때 오차가 큰 데이터 포인트의 비중을 높이고, 손실을 최소화하는 모델의 가중치를 구함
- 이전 학습기가 잘못 분류한 샘플에 가중치를 부여, 잔차를 직접 학습하지는 않음.
- weak learner는 랜덤 분류기보다 약간 더 성능이 좋아야 한다.
- 분류 모델들의 confidence level에 따라 가중합하여 최종 결정을 내린다. (신뢰도에 따라 가중치를 줘서 최종 예측)
- SVM을 내부 모델로 사용할 수 있다. (일반적으로는 Decision Stump = 깊이 1짜리 트리를 사용)
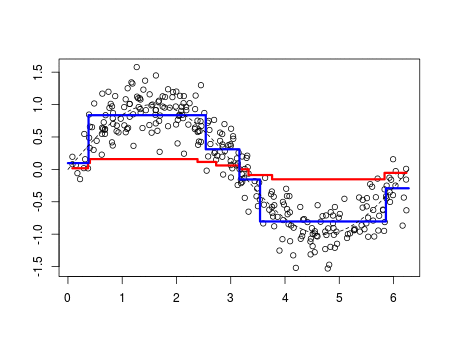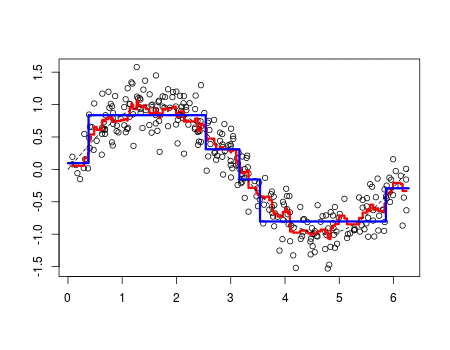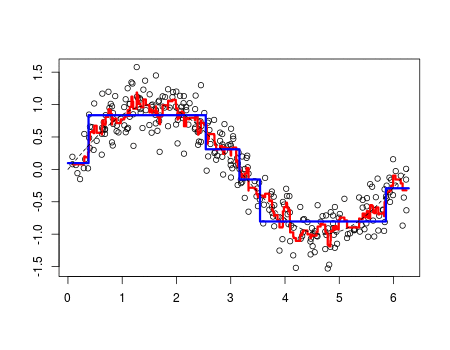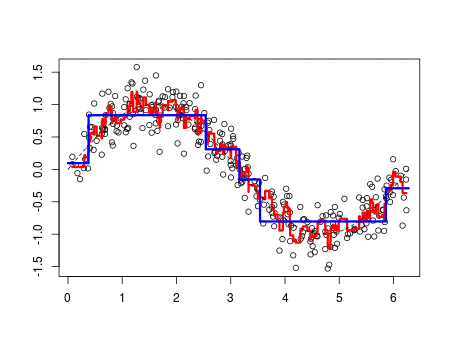
Gradient Boosting
- 잔여 오차에 새로운 예측기를 학습 → 모든 학생의 실수 패턴을 분석해서 더 집중해서 가르치기
- (오류 = 실제 값 - 예측 값)
- 실제 결과를 y, 피쳐를 x1, x2, ..., xn, 피처에 기반한 예측 함수를 F(x)라고 할 때,
- 오류식 h(x) = y - F(x)가 되고 이 식을 최소화하는 방향성을 가지고 반복적으로 가중치 값을 업데이트
- 단계별로 손실 함수를 줄여 나가기 때문에 병렬 처리가 불가능
- 이전 학습기의 잔차(residual)를 새로운 학습기의 목표값으로 사용
- 잔차에 대해 예측하는 모델을 추가하여 앙상블 모델을 구성
- 잔차는 loss function의 negative gradient와 같다. (잔차 = 실제값 - 예측값 : 자체가 gradient)
- 오차를 줄이기 위해 잔차(residual)를 모델링하는 방식을 경사 하강법으로 일반화한 방식 (잔차를 학습)
- 손실 함수로 동작하며 Negative Gradient를 잔차로 사용하여 모델을 학습
- 수행 시간이 느리고, 하이퍼 파라미터 튜닝이 어려움
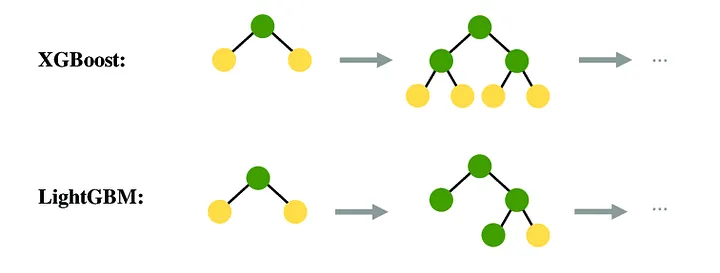
XGBoost
- Gradient Boosting의 개선 버전
- Gradient Boost에 비해 규제(L1, L2)가 가능하고 병렬처리도 가능하여 속도가 빠르다.
- 잔차 예측 + 2차 도함수(헤시안) 사용 (정확도↑)
- 과적합 규제 가능
- 나무 가지치기 기능 제공
- 자체 내장된 교차 검증
- 결손값 자체 처리
- 예측 오류가 더 이상 개선되지 않으면 조기 종료
주요 부스터 파라미터
- eta : default=0.3, learning rate와 같은 파라미터
- gamma : 트리의 리프 노드를 추가적으로 나눌지를 결정할 최소 손실 감소 값,
해당 값보다 큰 손실이 감소된 경우에만 리프 노드를 분리
- lambda : L2 Regularization 적용 값, 피처 개수가 많을 경우 적용 검토, 클수록 과적합 감소
- alpha : L1 Regularization 적용 값, 피처 개수가 많을 경우 적용 검토, 클수록 과적합 감소
과적합 문제가 심각하다면?
- eta를 낮춘다. (+ num_round, n_estimators는 높여야 한다.)
- max_depth를 낮춘다.
- min_child_weight 값을 높인다.
- gamma 값을 높인다.
LightGBM
- XGBoost보다 학습 시간이 적고, 메모리 사용량도 적은편
- 리프 중심 트리 분할(Leaf Wise)
ㄴ 최대한 균형 잡힌 트리를 유지하면서 분할하기 때문에 트리의 깊이가 최소화
ㄴ 균형 잡힌 트리를 유지하면서 분할하면 과적합에 더 강한 구조를 가지지만 균형을 맞추기 위한 시간이 많이 필요
ㄴ 리프 중심 트리는 최대 손실 값(max delta loss)을 가지는 리프 노드를 지속적으로 분할하여
트리의 깊이가 깊어지고 비대칭 트리가 생성된다.
- 카테고리형 피처의 자동 변환과 최적 분할 (원-핫 인코딩 불필요)
- 적은 데이터에서 과적합 발생 (10000건 이하)
스태킹 (Stacking)
- 여러 개의 서로 다른 모델(기본 학습기, base learners)의 예측 결과를 결합하여 최종 예측
- 각 base learner의 예측값을 모아서 새로운 데이터셋(2차 특징)을 생성.
- 이 데이터를 이용해 메타 학습기(meta learner)를 학습시키고, 최종 예측은 이 메타 모델이 수행.
- M x N 데이터 -> Model 1, 2, 3의 예측 값 M x 1개 씩 -> M x 3 결과 -> 다른 Model로 다시 학습
- 잔차를 학습하지는 않음.
- 과적합 방지를 위해 base 모델의 예측값은 반드시 검증 데이터에서 생성해야 함 (즉, Out-of-Fold 예측).
- 메타 모델이 base 모델의 잘못된 학습을 과대 평가하지 않도록 주의
- 계산 비용이 큼 (여러 모델 학습 필요).
- K-fold stacking: 훈련 데이터를 K개의 폴드로 나누어, 각 폴드에 대해 예측값을 생성.
- Blending: 훈련 데이터를 훈련/홀드아웃 세트로 나누고, 홀드아웃 예측값으로 메타 모델을 학습.
훈련 데이터
↓
[Model A] →
[Model B] → → 예측값 → 메타 모델 → 최종 예측
[Model C] →
| DT | RF | AdaBoost | Gradient | XGB | LightGBM | |
| 핵심 개념 | 단일 트리 | 트리 배깅 | 오분류 가중 부스팅 |
잔차 기반 순차 부스팅 |
GBM + 정규화 + 병렬 최적화 |
Leaf-wise 부스팅 + GPU 최적화 |
| 모델 특성 | 규칙 if-else | 여러 트리 평균 | 약한 학습기 조합 | 잔차 줄이기 반복 | 고속 + 규제 + 병렬화 | 매우 고속 + 대용량 |
| 예측 성능 | 낮음/불안정 | 안정적, 좋음 | 중간 | 좋음 | 매우 좋음 | 최고 수준 |
| 학습 속도 | 🚀 매우 빠름 | 🙂 중간 | 🙂 중간 | 😐 느림 | 👍 빠름 | 🚀 매우 빠름 |
| 예측 속도 | 🚀 빠름 | 😐 느림 (트리 多) | 🙂 중간 | 😐 중간 | 👍 빠름 | 👍 빠름 |
| 메모리 사용 | 👍 작음 | ❌ 큼 | 🙂 작음 | ❌ 큼 | 🙂 적절 | 🙂 적절 |
| 과적합 | ❌ 매우 높음 | 👍 낮음 | ❌ 다소 높음 | 😐 조절 필요 | 👍 규제로 낮음 | ⚠️ 과적합 가능 |
| 이상치 영향 | ❌ 매우 민감 | 🙂 덜 민감 | ❌ 매우 민감 | 😐 보통 | 🙂 적음 | 🙂 적음 |
| 대용량 데이터 | ❌ 부적합 | ❌ 메모리 폭발 가능 | 😐 가능 | 😐 다소 느림 | 👍 적합 | 🚀 매우 적합 |
| 결측치 처리 | ❌ X | ❌ X | ❌ X | ❌ X | 🟢 자동 처리 | 😐 제한적 지원 |
| 범주형 처리 | ❌ 인코딩 필요 | ❌ 인코딩 필요 | ❌ 인코딩 필요 | ❌ 인코딩 필요 | 😐 일부 버전 지원 | 🟢 카테고리 자동 |
| 해석 가능성 | 🟢 매우 높음 | ❌ 낮음 | 😐 낮음 | ❌ 낮음 | ❌ 낮음 | ❌ 낮음 |
| 규제 | 구조 제한 | 트리 개수로 간접 | 약함 | 약함 | 🟢 L1/L2 있음 | 🟢 L1/L2 있음 |
| 적합한 사용처 | 설명 필요/교육 | 일반적인 실전 문제 | 노이즈 적은 데이터 | 리소스 적은 부스팅 | 성능+안정 | 초대규모+고속 |
| 추천 | 초보/규칙 분석 | 대부분 데이터 | 노이즈 적은 환경 | GBM 기반 연구/실험 | 실무 전문가 | 대규모 AI 배포 |
페이스팅
- 훈련 세트의 중복을 허용하지 않은 샘플링
VotingClassifier
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.tree import DecisionTreeClassifier
from sklearn.svm import SVC
from sklearn.ensemble import VotingClassifier
from sklearn.metrics import accuracy_score
# 데이터셋 로드
X, y = load_iris(return_X_y=True)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
# 개별 모델 정의
clf1 = LogisticRegression(max_iter=1000, random_state=42)
clf2 = DecisionTreeClassifier(max_depth=4, random_state=42)
clf3 = SVC(probability=True, kernel='rbf', random_state=42)
# Hard Voting
hard_voting_clf = VotingClassifier(
estimators=[('lr', clf1), ('dt', clf2), ('svc', clf3)],
voting='hard'
)
# Soft Voting (SVC는 probability=True 옵션이 필요)
soft_voting_clf = VotingClassifier(
estimators=[('lr', clf1), ('dt', clf2), ('svc', clf3)],
voting='soft'
)
# 모델 학습
hard_voting_clf.fit(X_train, y_train)
soft_voting_clf.fit(X_train, y_train)
# 예측
y_pred_hard = hard_voting_clf.predict(X_test)
y_pred_soft = soft_voting_clf.predict(X_test)
# 정확도 출력
print("Hard Voting Accuracy:", accuracy_score(y_test, y_pred_hard))
print("Soft Voting Accuracy:", accuracy_score(y_test, y_pred_soft))
# 개별 출력
print(soft_voting_clf.classes_)
for name, clf in soft_voting_clf.named_estimators_.items():
print(name, clf.score(X_test, y_test))BaggingClassifier
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.svm import SVC
from sklearn.ensemble import BaggingClassifier
from sklearn.metrics import accuracy_score
# 데이터 로드
X, y = load_iris(return_X_y=True)
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.3, random_state=42
)
# 기본 분류기: SVC
base_svc = SVC(kernel='rbf', C=1.0, probability=True, random_state=42)
# BaggingClassifier로 SVC 앙상블
bagging_svc = BaggingClassifier(
base_estimator=base_svc,
n_estimators=20, # SVC 모델 20개
max_samples=0.8, # 각 모델이 80% 데이터만 학습
max_features=1.0, # 모든 feature 사용
bootstrap=True, # 복원추출
n_jobs=-1, # 병렬처리
oob_score=True, # OOB 평가 수행
random_state=42
)
# 학습
bagging_svc.fit(X_train, y_train)
# 예측
y_pred = bagging_svc.predict(X_test)
# 정확도 출력
print("SVC 단일 모델 정확도:", accuracy_score(y_test, SVC(kernel='rbf', C=1.0, probability=True, random_state=42).fit(X_train, y_train).predict(X_test)))
print("Bagging SVC 정확도:", accuracy_score(y_test, y_pred))
bagging_svc.oob_Bagging + Voting
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.tree import DecisionTreeClassifier
from sklearn.svm import SVC
from sklearn.ensemble import BaggingClassifier, VotingClassifier
from sklearn.metrics import accuracy_score
# 데이터 로드
X, y = load_iris(return_X_y=True)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
# 개별 분류기
clf1 = LogisticRegression(max_iter=1000, random_state=42)
clf2 = DecisionTreeClassifier(max_depth=4, random_state=42)
# BaggingClassifier (SVC 기반)
bagging_svc = BaggingClassifier(
estimator=SVC(probability=True, kernel='rbf', random_state=42),
n_estimators=10,
random_state=42
)
# VotingClassifier에 BaggingClassifier 포함
voting_clf = VotingClassifier(
estimators=[
('lr', clf1),
('dt', clf2),
('bagging_svc', bagging_svc)
],
voting='soft' # soft 투표 → SVC는 probability=True 필수
)
# 학습
voting_clf.fit(X_train, y_train)
# 예측
y_pred = voting_clf.predict(X_test)
# 정확도 출력
print("VotingClassifier (Bagging 포함) Accuracy:", accuracy_score(y_test, y_pred))GridSearchCV
from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split, GridSearchCV
from xgboost import XGBRegressor
from sklearn.metrics import mean_squared_error
import numpy as np
# 데이터 로드
X, y = fetch_california_housing(return_X_y=True)
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.2, random_state=42
)
# XGBRegressor (0.80 기준)
xgb = XGBRegressor(objective='reg:linear', random_state=42)
# GridSearchCV용 하이퍼파라미터 그리드
param_grid = {
'n_estimators': [100, 200],
'max_depth': [3, 5],
'learning_rate': [0.01, 0.1]
}
# GridSearchCV 설정
grid = GridSearchCV(
estimator=xgb,
param_grid=param_grid,
scoring='neg_mean_squared_error', # RMSE/MAE도 가능
cv=3,
n_jobs=-1,
verbose=1
)
# 학습
grid.fit(X_train, y_train)
# 최적 파라미터
print("Best Params:", grid.best_params_)
# CV RMSE
best_neg_mse = grid.best_score_
best_rmse = np.sqrt(-best_neg_mse)
print("Best CV RMSE:", best_rmse)
# 테스트셋 평가
y_pred = grid.best_estimator_.predict(X_test)
test_rmse = np.sqrt(mean_squared_error(y_test, y_pred))
print("Test RMSE:", test_rmse)
scoring
neg_mean_absolute_error, neg_mean_squared_error, r2
f1_macro, recall_macro, precision_macro, f1, recall, precision
RandomizedSerachCV
from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split, RandomizedSearchCV
from xgboost import XGBRegressor
from sklearn.metrics import mean_squared_error
from scipy.stats import randint, uniform
import numpy as np
# 데이터 로드
X, y = fetch_california_housing(return_X_y=True)
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.2, random_state=42
)
# XGBRegressor (0.80 기준)
xgb = XGBRegressor(objective='reg:linear', random_state=42)
# RandomizedSearchCV용 하이퍼파라미터 분포
param_dist = {
'n_estimators': randint(50, 300), # 50~300 사이 정수
'max_depth': randint(2, 10), # 2~10 사이 정수
'learning_rate': uniform(0.01, 0.3), # 0.01~0.31 균등분포
'subsample': uniform(0.7, 0.3), # 0.7~1.0
'colsample_bytree': uniform(0.7, 0.3) # 0.7~1.0
}
# RandomizedSearchCV 설정
random_search = RandomizedSearchCV(
estimator=xgb,
param_distributions=param_dist,
n_iter=20, # 샘플링 횟수
scoring='neg_mean_squared_error',
cv=3,
n_jobs=-1,
random_state=42,
verbose=1
)
# 학습
random_search.fit(X_train, y_train)
# 최적 파라미터
print("Best Params:", random_search.best_params_)
# CV RMSE
best_neg_mse = random_search.best_score_
best_rmse = np.sqrt(-best_neg_mse)
print("Best CV RMSE:", best_rmse)
# 테스트셋 평가
y_pred = random_search.best_estimator_.predict(X_test)
test_rmse = np.sqrt(mean_squared_error(y_test, y_pred))
print("Test RMSE:", test_rmse)
회귀 scoring 옵션
| scoring | 의미 | 비고 |
| r2 | 결정계수 R2 | 기본 회귀 평가 지표 |
| neg_mean_absolute_error | -MAE (평균 절대 오차) | MAE는 작을수록 좋으므로 부호 반전 |
| neg_mean_squared_error | -MSE (평균 제곱 오차) | 흔히 쓰는 손실 |
| neg_root_mean_squared_error | -RMSE (평균 제곱근 오차) | RMSE도 작을수록 좋으므로 부호 반전 |
| neg_mean_squared_log_error | -MSLE (평균 제곱 로그 오차) | 예측값과 실제값이 모두 양수일 때 |
| neg_median_absolute_error | -MedAE (중위 절대 오차) | 이상치(outlier)에 강건 |
| max_error | 최대 오차 | 하지만 부호 반전 안 함 |
| explained_variance | 설명 분산 | 분산 관점의 성능 평가 |
분류 scoring 옵션
| scoring | 의미 | 비고 |
| accuracy | 정확도 | 기본 지표, 맞춘 비율 |
| balanced_accuracy | 불균형 데이터용 정확도 | 클래스 불균형 보정 |
| precision | 정밀도 | 양성으로 예측한 것 중 실제 양성 비율 |
| recall | 재현율 | 실제 양성 중 예측 양성 비율 |
| f1 | F1-score | 정밀도와 재현율 조화평균, 이진 기본 |
| f1_micro | F1 (micro 평균) | 전체 샘플 기준 조화평균 |
| f1_macro | F1 (macro 평균) | 클래스별 F1 평균, 불균형 영향 없음 |
| f1_weighted | F1 (가중평균) | 클래스 비율 반영 |
| roc_auc | ROC-AUC | 확률 필요, 이진 분류 기본 |
| roc_auc_ovr | One-vs-Rest ROC-AUC | 다중 클래스 |
| roc_auc_ovo | One-vs-One ROC-AUC | 다중 클래스 |
| average_precision | PR-AUC | 확률 필요, 클래스 불균형 강건 |
| neg_log_loss | 음의 로그 손실 | 확률 예측 필요, 작을수록 좋음 (음수로 변환) |
| jaccard | 자카드 지수 | 이진/멀티클래스 |
| balanced_accuracy | 클래스 불균형 고려 | 불균형 데이터용 |
'개발 > Python' 카테고리의 다른 글
| 집합 연산 (0) | 2025.10.05 |
|---|---|
| groupby + agg로 여러 컬럼 집계하기 (0) | 2025.10.05 |
| T 검정 (0) | 2025.09.14 |
| datetime (0) | 2025.09.14 |
| LogisticRegression Hyper Parameters and Attributes (0) | 2025.09.14 |
댓글