평균에 대한 가설검정

가정
- 정규성 : 데이터가 정규분포를 따른다고 가정
- 연속형 데이터 : 데이터가 연속하고, 평균을 계산할 수 있어야 함.
- 독립성 : 두 지반의 데이터는 서로 독립적이어야 하고, 한 집단의 값이 다른 집단 값에 영향을 주면 안된다.
ttest_1samp (단일 표본 t-검정)
- 한 집단의 평균이 특정 값(모집단 평균)과 다른지 검정할 때 사용.
- ex) 한 학급 학생들의 시험 평균이 70점과 다른지 확인.
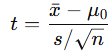
귀무/대립 가설
H₀ : sample_mean == popmean
H₁ : sample_mean != popmean
from scipy.stats import ttest_1samp
# 학생 시험 점수
scores = [68, 72, 75, 70, 69, 74, 73]
# 모집단 평균 70과 비교
t_stat, p_val = ttest_1samp(scores, popmean=70)
print("t-statistic:", t_stat) # 1.5768009924727366
print("p-value:", p_val) # 0.1659143165940077
정규성을 만족하지 않는 경우 - Wilcoxon 부호 순위 검정[비모수], scipy.stats.wilcoxon(data - 기대값, alternative)
ttest_ind (독립 표본 t-검정)
- 두 독립된 집단의 평균이 서로 다른지 검정할 때 사용.
- 예: 남학생과 여학생의 수학 점수 평균 비교.
- 두 집단의 분산이 같은 경우 (eqaul_var=True) : 독립 표본 t-검정 (Student's t-test)


- 두 집단의 분산이 다른 경우 (eqaul_var=False) : Welch's t-test
귀무/대립 가설
H₀ : mean_group1 == mean_group2
H₁ : mean_group1 != mean_group2
from scipy.stats import ttest_ind
# 남학생, 여학생 점수
male_scores = [68, 72, 75, 70, 69]
female_scores = [74, 77, 73, 75, 76]
# equal_val=True, 두 집단의 분산이 같다고 가정
t_stat, p_val = ttest_ind(male_scores, female_scores, equal_var=True)
print("t-statistic:", t_stat) # -2.940588176458822
print("p-value:", p_val) # 0.018692816860882495
등분산성을 만족하지 않는 경우 - Welch's t-검정[모수], eqaul_var=False

정규성(+ 등분산성)을 만족하지 않는 경우 - scipy.stats.mannwhitneyu(A, B, alternative='two-sided')

ttest_rel (대응 표본 t-검정)
- 같은 대상이 두 조건에서 측정되었을 때 평균 차이를 검정.
- 예: 다이어트 전후 체중 변화, 약물 투여 전후 혈압 변화.

귀무 / 대립 가설
H₀ : mean_diff == 0
H₁ : mean_diff != 0
from scipy.stats import ttest_rel
# 다이어트 전후 체중
before = [80, 75, 78, 90, 85]
after = [78, 73, 77, 88, 84]
t_stat, p_val = ttest_rel(before, after)
print("t-statistic:", t_stat) # 6.531972647421809
print("p-value:", p_val) # 0.002837845926734446
정규성을 만족하지 않는 경우 - Wilcoxon의 부호 순위 검정, scipy.stats.wilcoxon(after, before)
양측 검정 vs 단측 검정
import numpy as np
from scipy.stats import ttest_rel
before = np.array([70, 75, 68, 72, 74])
after = np.array([75, 78, 70, 76, 77])
stat, pvalue = ttest_rel(after, before)
print(stat, pvalue) # 6.667948594698257 0.0026285451076807544
p-value가 양측 검정의 절반이 된다.
stat, pvalue_two = ttest_rel(after, before)
pvalue_one = pvalue_two / 2 if stat > 0 else 1 - pvalue_two / 2
print(stat, pvalue_one) # 6.667948594698257 0.0013142725538403772
pvalue_one_left = pvalue_two / 2 if stat < 0 else 1 - pvalue_two / 2
pvalue_one_left # 0.9986857274461596

우측 단측 검정은 차이가 + 방향(증가)” 인지를 보는 검정
H₀: μ(after−before) ≤ 0
H₁: μ(after−before) > 0
stat < 0이라면 표본 평균차이가 오히려 감소 방향이라는 뜻이므로, 우측 검정에서 유리한 증거가 전혀 없다.
p-value는 큰 값(1에 가까움) 이 나와야 정상
즉, p-value = 1 - (p_one / 2)
예시 코드
import numpy as np
from scipy.stats import ttest_rel
before = np.array([70, 75, 68, 72, 74])
after = np.array([75, 78, 70, 76, 77])
stat, p_two = ttest_rel(after, before)
p_right = p_two/2 if stat > 0 else 1 - p_two/2
p_left = p_two/2 if stat < 0 else 1 - p_two/2
print("t-statistic =", stat) # 6.667948594698257
print("two-sided p =", p_two) # 0.0026285451076807544
print("right-tailed p (after > before) =", p_right) # 0.0013142725538403772
print("left-tailed p (after < before) =", p_left) # 0.9986857274461596'개발 > Python' 카테고리의 다른 글
| groupby + agg로 여러 컬럼 집계하기 (0) | 2025.10.05 |
|---|---|
| 앙상블 (Ensemble) (0) | 2025.09.14 |
| datetime (0) | 2025.09.14 |
| LogisticRegression Hyper Parameters and Attributes (0) | 2025.09.14 |
| 카이제곱 검정 (0) | 2025.09.14 |


댓글