SW 역량테스트 합격하기 A형 강의 오픈!! (인프런 바로가기)
참고
- 우선순위 큐 응용 (1) - 두 개의 heap을 이용하여 중앙값 찾기
- 우선순위 큐 응용 (2) - 최댓값, 최솟값 동시에 관리하기
- BOJ 1655 : 가운데를 말해요 with 세그먼트 트리

가운데라는 값은 우선순위로 두기 굉장히 애매하다.
이유는 가장 높은 우선순위의 가운데와 최악의 가운데를 정의할 수 없기 때문이다.
만약 어떤 값들 중, 가운데 값을 pop한다고 하자.
그러면 heap[hn--] 에서 최악의 가운데 값을 넣어야 하는데,
이 값은 남아있는 값들 중에서 가운데를 정의하게 되므로, 매번 값이 바뀐다.
따라서 가장 가운데의 우선순위는 heap 하나로는 결정할 수 없다.
그러나 heap을 2개 이용하면 가운데 값을 우선순위로 정할 수 있다.
전체 input 값을 절반으로 나누고, 작은 값의 절반을 최대 힙, 큰 값의 절반을 최소 힙으로 넣어야 한다.
최대 힙과 최소 힙을 같은 개수로 유지하되, 홀수인 경우에는 최소 힙에 하나 더 넣을 수 있다고 가정하자.
그러면 가운데 값의 후보는 작은 값들이 모인 최대 힙과 큰 값들이 모인 최소 힙의 가장 큰 우선순위의 값이 된다.
예를 들어, 예제 입력 1의 1, 5, 2, 10, -99, 7, 5를 보자.
-99, 1, 2, 5, 5, 7, 10을 위의 조건대로 나누면
최대 힙에는 현재 -99, 1, 2가 들어가 있고, 최소 힙에는 5, 5, 7, 10이 들어가 있게 된다.
이때, 가운데 값은 반드시 최소 힙의 우선순위가 가장 높은 값인 5가 된다.
input의 개수가 짝수인 경우를 보자.
→ 1, 2, 3, 4, 5, 6, 7, 8
최대 힙에는 1, 2, 3, 4가 있고, 최소 힙에는 5, 6, 7, 8있다.
이제 가운데 값의 후보는, 최대 힙의 우선순위가 가장 큰 값인 4와 최소 힙의 우선순위가 가장 큰 값인 5가 된다.
짝수인 경우는 두 값 중 작은 값을 출력하라고 하였으므로, 4가 답이 된다.
그림으로 예제 입력 1을 한 개씩 받으면서 최대 힙과 최소 힙이 어떻게 변하는지 보자.
[1, 5, 2, 10, -99, 7, 5]
첫번 째 input 1
최소 힙과 최대 힙이 모두 0이므로 "홀수인 경우에는 최소 힙에 하나 더 넣을 수 있다" 조건에 의해 최소 힙에 1을 넣자.

input의 갯수가 홀수인 경우 가운데 값은 최소 힙의 우선순위가 가장 높은 값으로
minHeap[1] = 1을 출력한다.
[1, 5, 2, 10, -99, 7, 5]
두번 째 input 5
5를 입력 받았는데, 개수를 맞추기 위해 무작정 최대 힙에 넣어서는 안된다.
"작은 값의 절반을 최대 힙, 큰 값의 절반을 최소 힙으로 넣어야 한다" 조건에 의해
1은 최대 힙에, 5는 최소 힙에 들어가야 한다.
즉, 최대 힙에 넣기 전에 최소 힙의 우선순위와 비교를 하여, 교환이 필요하면 교환해준다.
if (minHeap[1] < input) /* 들어온 값이 최소 힙보다 크다면 */
{
maxPush(maxHeap, maxHn, minPop(minHeap, minHn)); /* 최소 힙의 값을 빼서 최대 힙에 넣는다 */
minPush(minHeap, minHn, input); /* 최소 힙에 다시 input을 넣는다 */
}
else
{
maxPush(maxHeap, maxHn, input); /* 최소 힙보다 작으면 최대 힙에 넣는다 */
}
이때, 가운데 값은 두 값 중 더 작은 값인 maxHeap[1] = 1이 된다.
(maxHeap[1]이 minHeap[1] 보다 클 수 없다. 큰 값을 최소 힙에 넣기 때문이다.)
[1, 5, 2, 10, -99, 7, 5]
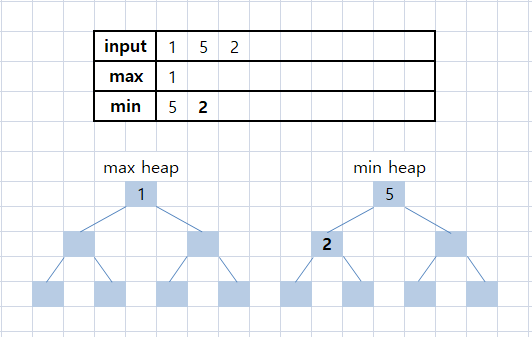
세번 째 input 2
input의 개수가 홀수이므로 최소 힙에 넣어야 한다.
그리고 들어가는 input이 최대 힙의 우선순위보다 크므로 최소 힙에 그대로 넣는다.
if (input < maxHeap[1]) /* 들어온 값이 최대 힙보다 작다면 */
{
minPush(minHeap, minHn, maxPop(maxHeap, maxHn)); /* 최대 힙의 값을 빼서 최소 힙에 넣는다 */
maxPush(maxHeap, maxHn, input); /* 최대 힙에 다시 input을 넣는다 */
}
else
{
minPush(minHeap, minHn, input); /* 최대 힙보다 크다면 최소 힙에 넣는다 */
}
그런데 최소 힙에 push를 하였으니, hn을 부모와 계속 비교하면서 우선순위를 갱신해야 한다.
최종 그림은 아래와 같게 된다.
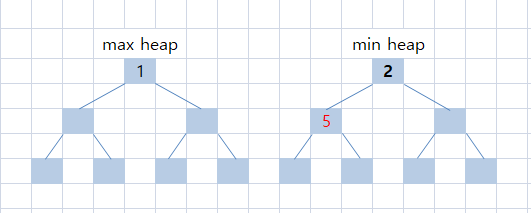
마찬가지로, 홀수인 경우의 가운데 값은 minHeap[1] = 2가 된다.
[1, 5, 2, 10, -99, 7, 5]
네번 째 input 10
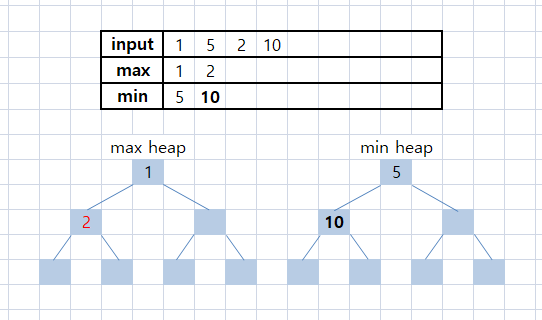
10은 minHeap[1] = 2보다 큰 값이므로, 무작정 넣어서는 안된다.
교환이 일어나게 되는데, 최소 힙에서 pop을 하였으므로 5가 minHeap[1]이 된다.
그리고 minHeap[2]가 10으로 들어오고, maxHeap[2] = 2가 된다.
이때, 최대 힙은 우선순위가 갱신된다.
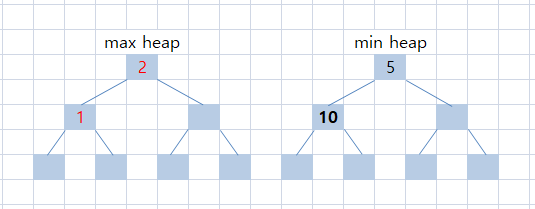
여전히 짝수일 때 가운데 값은 maxHeap[1] = 2 임을 알 수 있다.
[1, 5, 2, 10, -99, 7, 5]
다섯번 째 input -99
갑자기 굉장히 작은 값이 들어왔다. 홀수의 경우, 최소 힙에 들어가야 되지만,
maxHeap[1]보다 -99가 더 작으므로, 교환이 일어나게 된다.
maxHeap[1]을 pop해주고 minHeap에 push해야 한다.

최대 힙에서 pop을 했기 때문에 1이 maxHeap[1]로 이동하게 되었고,
minHeap에 pop했던 2를 push했기 때문에 minHeap[3]에는 2가 들어간다.
그리고 minHeap의 우선순위를 갱신한다.
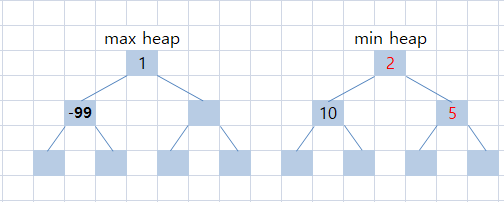
홀수인 경우의 가운데 값은 minHeap[1] = 2임을 알 수 있다.
[1, 5, 2, 10, -99, 7, 5]
모든 input을 넣으면 아래와 같은 heap이 된다.
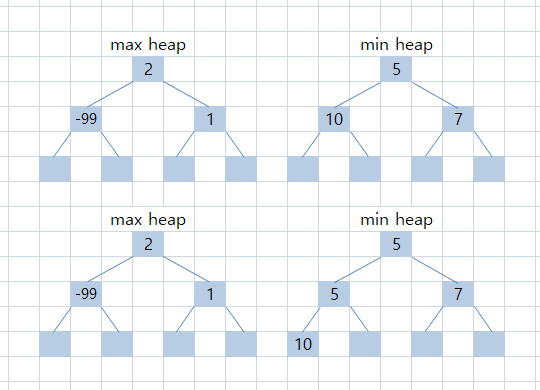
짝수인 경우는 maxHeap[1]이, 홀수인 경우는 minHeap[1]이 가운데 값임을 알 수 있다.
최종 코드는 아래와 같다.
#include <stdio.h>
int N;
int minHeap[100100];
int minHn;
int maxHeap[100100];
int maxHn;
int maxPop(int* heap, int& hn)
{
register int tmp, ret;
ret = heap[1];
heap[1] = heap[hn];
heap[hn--] = -10001;
for (register int i = 1; i * 2 <= hn;)
{
if (heap[i] > heap[i * 2] && heap[i] > heap[i * 2 + 1]) break;
else if (heap[i * 2] > heap[i * 2 + 1])
{
tmp = heap[i * 2];
heap[i * 2] = heap[i];
heap[i] = tmp;
i = i * 2;
}
else
{
tmp = heap[i * 2 + 1];
heap[i * 2 + 1] = heap[i];
heap[i] = tmp;
i = i * 2 + 1;
}
}
return ret;
}
void maxPush(int* heap, int& hn, int x)
{
register int tmp;
heap[++hn] = x;
for (register int i = hn; i > 1; i /= 2)
{
if (heap[i / 2] > heap[i]) break;
tmp = heap[i / 2];
heap[i / 2] = heap[i];
heap[i] = tmp;
}
}
int minPop(int* heap, int& hn)
{
register int tmp, ret;
ret = heap[1];
heap[1] = heap[hn];
heap[hn--] = 10001;
for (register int i = 1; i * 2 <= hn;)
{
if (heap[i] < heap[i * 2] && heap[i] < heap[i * 2 + 1]) break;
else if (heap[i * 2]< heap[i * 2 + 1])
{
tmp = heap[i * 2];
heap[i * 2] = heap[i];
heap[i] = tmp;
i = i * 2;
}
else
{
tmp = heap[i * 2 + 1];
heap[i * 2 + 1] = heap[i];
heap[i] = tmp;
i = i * 2 + 1;
}
}
return ret;
}
void minPush(int* heap, int& hn, int x)
{
register int tmp;
heap[++hn] = x;
for (register int i = hn; i > 1; i /= 2)
{
if (heap[i / 2] < heap[i]) break;
tmp = heap[i / 2];
heap[i / 2] = heap[i];
heap[i] = tmp;
}
}
int main(void)
{
int input;
scanf("%d", &N);
scanf("%d", &input);
minPush(minHeap, minHn, input);
printf("%d\n", input);
for (int i = 1; i < N;i++)
{
scanf("%d", &input);
if (maxHn == minHn) /* 현재 짝수개인 경우 */
{
if (input < maxHeap[1])
{
minPush(minHeap, minHn, maxPop(maxHeap, maxHn));
maxPush(maxHeap, maxHn, input);
printf("%d\n", minHeap[1]);
}
else
{
minPush(minHeap, minHn, input);
printf("%d\n", minHeap[1]);
}
}
else /* 현재 홀수개인 경우 */
{
if (minHeap[1] < input)
{
maxPush(maxHeap, maxHn, minPop(minHeap, minHn));
minPush(minHeap, minHn, input);
printf("%d\n", maxHeap[1]);
}
else
{
maxPush(maxHeap, maxHn, input);
printf("%d\n", maxHeap[1]);
}
}
}
return 0;
}
'알고리즘 > [PRO] 삼성 SW 역량 테스트 B형' 카테고리의 다른 글
| 해시 응용 : 2차원 배열 탐색 (5) | 2021.03.09 |
|---|---|
| 데이터의 추가, 삭제, 수정, 검색 - 해시 테이블 응용 (0) | 2021.02.28 |
| BOJ 10825 : 국영수 (1) | 2021.02.21 |
| BOJ 11286 : 절댓값 힙 (0) | 2021.02.21 |
| BOJ 11279 : 최대 힙 (1) | 2021.02.21 |





댓글