A형 필수 알고리즘을 체계적으로 배우고 싶다면? (인프런 바로가기)
참고
- 우선순위 큐 Priority Queue
- 우선순위 큐 응용 (1) - 두 개의 heap을 이용하여 중앙값 찾기
- 우선순위 큐 응용 (2) - 최댓값, 최솟값 동시에 관리하기
B형에서 Merge Sort는 마지막에 이분 탐색을 위해 필요한 경우가 많다.
그리고 '무언가'를 push해주고, 그 중 가장 우선순위가 높은 '무언가'를 pop하면서,
순서를 유지하고 싶을 때는 우선순위 큐를 이용해야된다.
요즘 B형에서는 HashTable + 우선순위 큐 모두 사용해야하는 경우가 많으므로,
우선순위 큐에 대해서 익혀보자.
먼저 우선순위 큐 코드를 자유롭게 사용하고 싶으면, 그림을 그려가면서 직접 만들어보는 게 좋다.
우선순위 큐는 heap으로 만든다.
heap을 위한 1차원 배열을 선언하고, heap index = hn을 만들자.
int heap[16];
int hn;hn은 최초로 0이다. 따라서 heap이 비어있는지는 if(hn)으로 확인할 수 있다.
heap[16]을 아래의 그림처럼 생각해야 된다. 이때 쉬운 index 관리를 위해 heap[0]은 버린다.

이렇게 heap을 관리하면 heap을 내려가거나 올라갈 때가 쉽다.
예를 들어서 heap[ i = 5 ] 라고 가정하자.
i = 5에서 자식 node(10, 11)로 이동하려면, i * 2 또는 i * 2 + 1을 하면 된다.
i = 5에서 부모 node(2) 로 이동하려면, i / 2를 하면 된다.
마찬가지로 모든 i에 대해서 자식 node는 i * 2, i * 2 + 1이 되고,
부모 node는 i / 2로 하면 된다.
이제 heap에 값을 순서대로 입력해보면서 push를 구현해보자.

최초로 hn = 0이므로 hn을 먼저 1로 만들어주고 x = 5를 넣어야 한다.
heap[++hn] = x; /* x = 5 */
그리고 6을 넣어보자. 지금 만들려고 하는 heap은 최소 heap이다.
즉, 우선 순위가 높다 = 가장 작은 값이 heap[1]에 있어야 되는 것을 의미한다.
heap[++hn] = x; /* x = 6 */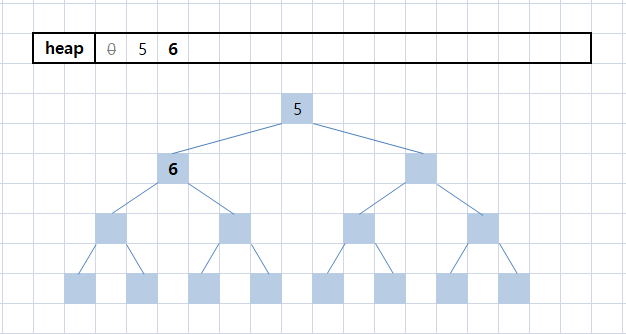
6을 넣었으니 비교를 해줘야 한다.
6이 부모 node와 비교해서 우선순위를 만족하는 지 체크해야 한다.
hn = 2이므로, 6의 부모 node는 hn / 2 = 1이 된다.
heap[hn = 2] = 6 > heap[hn = 1] = 5 이므로, 우선순위를 만족해서 변동이 없다.
이제 4를 push해보자.
heap[++hn] = x; /* x = 4 */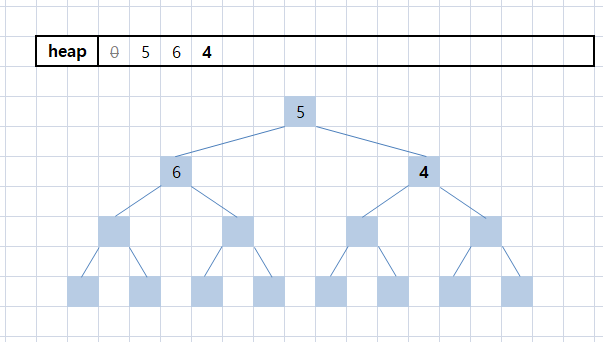
hn = 3이 되고, hn의 부모는 hn / 2 = 1이 된다.
그런데 heap[hn = 3] = 4 > heap[hn = 1] = 5 를 만족하지 않는다.
따라서 heap을 갱신해야 된다.
heap을 갱신할 때는, 우선순위를 계속 만족할 때 까지, 부모와 바꿔주면 된다.
따라서 for문을 이용하여 i = hn부터 i > 1을 만족할 때 까지 바꾼다.
for (int i = hn; i > 1; i /= 2)
{
/* 부모 node <= 자식 node */
if (heap[i / 2] <= heap[i]) break; /* heap을 만족하면 종료 */
/* 만족할 때 까지 교환 */
tmp = heap[i / 2];
heap[i / 2] = heap[i];
heap[i] = tmp;
}
heap[i / 2 = hn / 2 = 1] <= heap[3]을 만족하지 않으므로, tmp를 이용해 교환하게 된다.
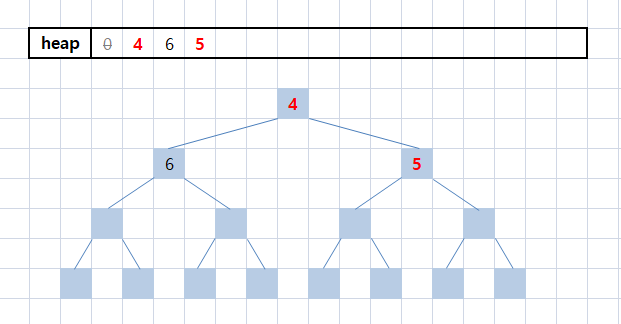
다시 i /= 2에 의해 i = 1이 되고, 더 이상 비교할 부모가 없으므로 종료된다.
6과 5는 비교할 필요가 없다. heap은 항상 자식과 부모를 비교하기만 하면, 우선순위가 보장이 된다.
이제 -1을 push해 보자.
heap[++hn] = x; /* x = -1 */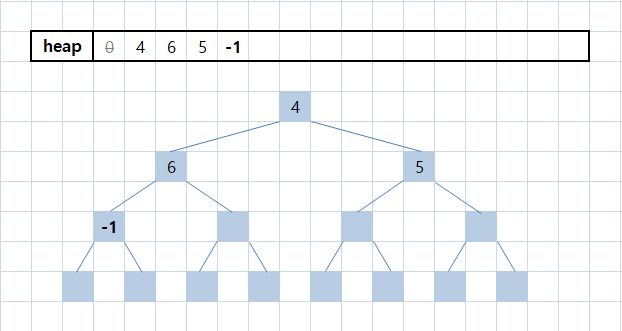
hn = 4가 되고 heap[4] = -1이 된 상태이다.
부모 node는 hn / 2 = 2가 되고
heap[hn / 2 = 2] <= heap[4] (6 <= -1)을 만족하지 않으므로, tmp를 이용해 다시 교환해야 한다.
for문을 이용해 바꿔보자. i = hn = 4, i / 2 = 2가 된다.
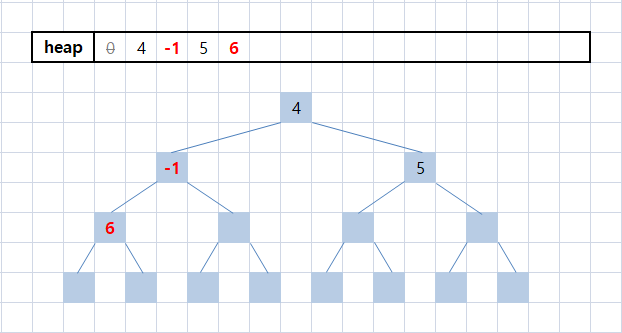
heap에 의해 위치가 변경되었고 i /= 2에 의해 i = 2가 되었다.
i = 2의 부모인 i / 2 = 1과 비교를 해보자.
heap[i / 2 = 1] <= heap[2] (4 <= -1)도 여전히 만족하지 않으므로, heap이 갱신된다.

이제 i = 1이 되었으므로 종료하게 된다.
마지막으로 3를 push해보자.
heap[++hn] = x; /* x = 3 */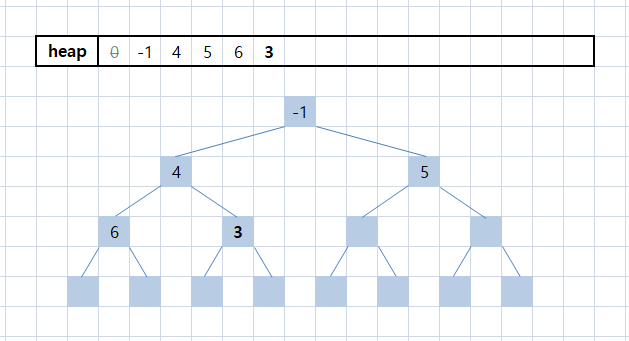
hn = 5가 되고 hn의 부모는 다시 hn / 2 = 2가 된다.
heap[hn / 2 = 2] <= heap[5] (5 <= 3) 를 만족하지 않는다. 따라서 갱신이 일어난다.
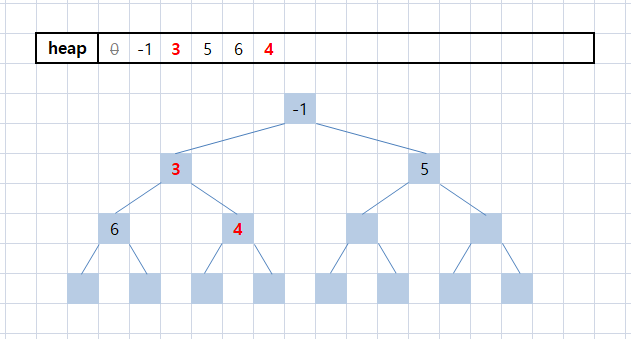
i = 2가 되고 heap[i / 2 = 1] <= heap[i = 2] (-1 <= 3)을 만족하므로, break에 의해 종료된다.
여기에서 heap[3] = 5이고 heap[5] = 4인 것을 확인해보자.
값이 큰 5가 4보다 위의 Level에 있어서, 우선순위가 틀린 것처럼 보일 수도 있다.
하지만 heap은 부모 자식 간에만 우선순위를 만족해주기만 하면 된다.
heap[3]과 heap[5]는 부모 자식관계가 아니므로 (i = 3 의 자식은 i * 2 = 6과 i * 2 + 1 = 7이다.)
우선순위는 여전히 유지된다.
최종 push 코드는 아래와 같다. 여러 heap을 사용하기 위해 포인터와 참조자를 이용해서 구현하면 편하다.
void push(int* heap, int& hn, int x)
{
int tmp;
heap[++hn] = x;
for (int i = hn; i > 1; i /= 2)
{
if (heap[i / 2] <= heap[i]) break;
tmp = heap[i / 2];
heap[i / 2] = heap[i];
heap[i] = tmp;
}
}
이제 pop을 구현해보자.
현재의 heap에서 pop을 하면 -1이 된다. -1을 빼고 나면 우선순위가 어떻게 변해야 될까?
현재 heap에서 -1 다음으로 작은 값은 3이다.
pop은 아래와 같이 구현되는데, 최종적으로 3이 heap[1]에 오게 되는지 확인해보자.
1) pop의 return값 heap[1]을 기억해둔다.
2) heap의 배열에서 가장 끝에 값, 즉 heap[hn]을 heap[1]로 변경한다.
3) heap[hn]은 최악의 우선순위값(최소힙이므로 0x7fff0000 정도의 큰 값)으로 변경해둔다.
4) heap이 1개 줄었으므로 hn 을 1 감소 시킨다.
ret = heap[1]; /* 1) */
heap[1] = heap[hn]; /* 2) */
heap[hn--] = 0x7fff0000; /* 3) ~ 4) */
그림으로 구현을 여기까지의 구현을 확인해보자.
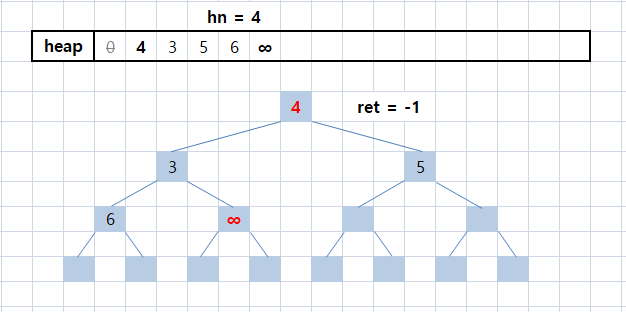
0x7fff0000을 무한대 ∞로 표시하였다. 실제 최악의 값은 입력 값의 범위에 따라 바뀔 수 있다.
이제 hn = 1부터 시작하여 자식 node를 훑어가면서 heap을 갱신한다.
자식 node 2개 중 우선순위가 더 큰 값(더 작은 값)을 바꿔주면 heap을 유지하게 된다.
for (int i = 1; i * 2 <= hn;)
{
/* 자식 node 모두 비교해서 자신이 작다면 우선순위를 만족 종료. */
if (heap[i] < heap[i * 2] && heap[i] < heap[i * 2 + 1]) break;
else if (heap[i * 2] < heap[i * 2 + 1]) /* 왼쪽 node가 더 작다면 */
{
tmp = heap[i * 2];
heap[i * 2] = heap[i];
heap[i] = tmp;
i = i * 2;
}
else /* 오른쪽 node가 더 작다면 */
{
tmp = heap[i * 2 + 1];
heap[i * 2 + 1] = heap[i];
heap[i] = tmp;
i = i * 2 + 1;
}
}
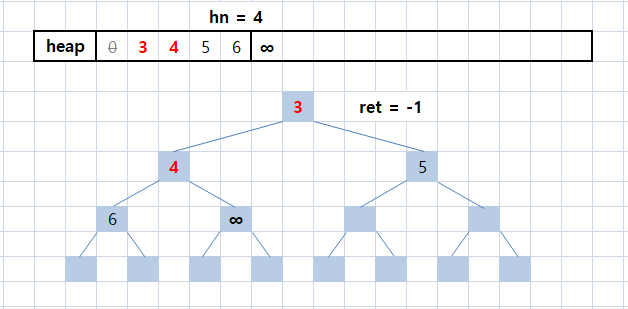
i = 1에서 왼쪽 node = 4와 오른쪽 node = 5 중 왼쪽이 더 작으므로, 왼쪽과 자리를 바꾸게 되고,
i = 2가 된다.
i = 2가 되어 자식 node의 index는 4와 5가 되지만, hn은 현재 4가 된다.
그런데 자식 node 중에 hn 이하인 것만 검사하는 코드보다는, 자식 node 모두를 비교하는 것이 편하다.
이러한 이유로 최초에 heap[hn] = 0x7fff0000 코드가 들어가게 된다.
index 5에는 이미 최악의 우선순위(∞)가 들어있어서 갱신이 되지 않는다.
최종 코드는 아래와 같고, B형에서 속도 향상을 위해 register를 쓰는 것을 잊지말자.
int heap[16];
int hn;
int pop(int* heap, int& hn)
{
register int tmp, ret;
ret = heap[1];
heap[1] = heap[hn];
heap[hn--] = 0x7fff0000;
for (register int i = 1; i * 2 <= hn;)
{
if (heap[i] < heap[i * 2] && heap[i] < heap[i * 2 + 1]) break;
else if (heap[i * 2] < heap[i * 2 + 1])
{
tmp = heap[i * 2];
heap[i * 2] = heap[i];
heap[i] = tmp;
i = i * 2;
}
else
{
tmp = heap[i * 2 + 1];
heap[i * 2 + 1] = heap[i];
heap[i] = tmp;
i = i * 2 + 1;
}
}
return ret;
}
void push(int* heap, int& hn, int x)
{
register int tmp;
heap[++hn] = x;
for (register int i = hn; i > 1; i /= 2)
{
if (heap[i / 2] <= heap[i]) break;
tmp = heap[i / 2];
heap[i / 2] = heap[i];
heap[i] = tmp;
}
}
이렇게 그림을 그려가면서 heap을 구현해두면 응용하기가 편하다.
heap의 우선순위를 check하는 부분과 heap[hn--] = 최악의 값을 수정하면
최소 힙, 최대 힙, 절댓값 힙, 구조체인 경우 등을 모두 만들 수 있다.
int pop(int* heap, int& hn)
{
...
heap[hn--] = 0x7fff0000;
for (register int i = 1; i * 2 <= hn;)
{
if (heap[i] < heap[i * 2] && heap[i] < heap[i * 2 + 1]) break;
else if (heap[i * 2] < heap[i * 2 + 1])
...
}
...
}
void push(int* heap, int& hn, int x)
{
...
for (register int i = hn; i > 1; i /= 2)
{
if (heap[i / 2] <= heap[i]) break;
...
}
}연습 문제는 아래 링크를 참고하자.
최소 힙 - 위 예시에 대한 문제 연습
최대 힙 - if / else의 조건 변경 + heap[hn]에 최악의 값 넣기 연습.
절댓값 힙 - if / else의 조건 변경 + heap[hn]에 최악의 값 넣기 연습.
가운데를 말해요 - heap 2개를 이용하여 가운데 값을 우선 순위가 높아지도록 만들기.
이중 우선순위 큐 - heap 2개를 이용하여 최솟값과 최댓값 동시에 관리하기.
국영수 - 구조체에 대한 if / else 조건 변경 + heap[hn]에 최악의 값 넣기 연습.
+ 우선순위 큐에서 임의 원소 삭제 방법은 링크에서 확인해보자.
+ 우선순위 큐에서 임의 원소 갱신 방법은 링크에서 확인해보자.
'알고리즘 > [PRO] 삼성 SW 역량 테스트 B형' 카테고리의 다른 글
| BOJ 11279 : 최대 힙 (1) | 2021.02.21 |
|---|---|
| BOJ 1927 : 최소 힙 (3) | 2021.02.21 |
| BOJ 7785 : 회사에 있는 사람 (Hash Table + Merge Sort) (0) | 2021.02.18 |
| 삼성 B형 샘플 문제 : 숫자야구게임 (+ Linked List 삭제) (2) | 2021.02.17 |
| BOJ 1764 : 듣보잡 (Hash Table + Merge Sort) (0) | 2021.02.17 |





댓글