- 통계적 가설 검정은 귀무가설이 참이라고 가정
- 이 가정 하에 관측된 통계량이 얼마나 극단적인지, 기각역에 속할 확률을 평가
- 관측 통계량이 기각역에 위치한다면, 귀무가설이 기각된다.
유의수준 (α, alpha)
정의 : 귀무가설 H0가 맞는데, 잘못 기각할 확률 (즉 1종 오류 확률)
- 흔히 0.05, 0.01 같은 값으로 설정
- 직관적 의미 : "나는 잘못된 결론을 내릴 위험을 최대 5%만 허용하겠다."
p-value
정의: 관찰된 데이터가 귀무가설 하에서 나올 확률
- p-value < α이면 귀무가설 기각
- 귀무가설이 참일 때 관측된 통계량 이상으로 극단적인 값을 얻을 확률
- 직관적 의미 : "내가 관찰한 데이터가 우연히 나올 확률이 이 정도인데, 너무 낮으니까 H0를 버리자."
검정력 (Power, 1 - β)
정의 : 대립가설 H1이 맞을 때 귀무가설을 정확히 기각할 확률
- 여기서 β는 2종 오류(Type II error) 확률, 즉 H1이 맞는데 H0를 놓치는 확률
- 직관적 의미 : "실제로 효과가 있으면 내가 그걸 발견할 확률이 얼마나 될까?"
- 검정력은 α, 표본크기, 효과크기, 변동성 등에 따라 달라짐.

α는 "실수 허용 범위"
p-value는 "데이터가 얼마나 극단적인가"
검정력은 "진짜 효과를 얼마나 잘 잡는가"
α 기준 : 귀무가설 H0가 맞을 때
- α = H0 맞는데 잘못 기각할 확률 (1종 오류)
- 관찰값이 α보다 극단적이면 귀무가설 기각 → 대립가설 채택
- 여기서는 H1가 맞는지 여부는 아직 모르는 상태입니다.
검정력 (1-β) : 대립가설 H1가 맞을 때
- 1-β = H1일 때 귀무가설을 올바르게 기각할 확률
- 실제로 H1가 맞으면 α에서 결정된 임계값 기준으로 귀무가설을 기각할 확률이 바로 검정력
- 즉, 관찰값이 H0 기준으로 기각되었는지 여부는 이미 결정됨,
검정력은 H1가 맞았을 때 성공 확률을 계산하는 통계적 개념
예시 상황
- 목표 : 다이어트 약이 체중 감량에 효과가 있는지 검정
- 귀무가설 H0: "약은 체중 감량 효과가 없다"
- 대립가설 H1: "약은 체중 감량 효과가 있다"
- 표본 평균 체중 변화로 검정
- α = 0.05 (5% 잘못된 기각 허용)
α (1종 오류) 예시
상황 : 실제로 약이 효과가 없는 경우(H0가 맞음)
표본 데이터를 측정했더니, 평균 감량이 통계적으로 충분히 크다고 나왔다
α = 0.05 → 이 경우 귀무가설을 잘못 기각할 확률이 5%
결과 해석 : "데이터가 우연히 극단적으로 나와서 약이 효과 있다고 잘못 판단할 수도 있다"
시각적으로는 H0 분포의 오른쪽 꼬리 영역이 α 영역
β (2종 오류) / 검정력 (1-β) 예시
- 상황 : 실제로 약이 효과가 있음(H1가 맞음)
- 하지만 표본 평균이 충분히 크지 않아 귀무가설이 채택될 수도 있음 → 이게 β, 2종 오류
- 검정력 1-β = H1가 맞을 때 귀무가설을 정확히 기각할 확률
- 직관적 의미 : "약이 효과가 실제로 있으면, 우리가 실험에서 이를 발견할 확률이 얼마나 되는가"
- 시각적으로는 H1 분포에서 임계값 오른쪽 초록 영역이 검정력, 왼쪽 빨간 영역이 β
α와 1-β가 왜 다른가?
- α = 0.05 → H0 기준으로 임계값을 정함
- 실제 약이 효과가 있으면(H1 기준) → 이 임계값으로 귀무가설을 얼마나 잘 기각할 수 있는가가 검정력
- 이미 α 기준으로 귀무가설을 기각했다면, "검정력"은 사실상 H1에서 이 임계값으로 잘 잡히는 정도를 말함
- 따라서 α와 1-β를 단순히 더하면 1이 아님
- β + 1-β = 1 → H1 기준에서는 성립
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
# 파라미터 설정
mu0 = 0 # H0 평균
mu1 = 1 # H1 평균
sigma = 1 # 표준편차
alpha = 0.05 # 유의수준
# 임계값 계산 (단측검정 가정)
z_alpha = norm.ppf(1 - alpha)
x = np.linspace(-3, 4, 1000)
# H0, H1 확률밀도
pdf_H0 = norm.pdf(x, mu0, sigma)
pdf_H1 = norm.pdf(x, mu1, sigma)
plt.figure(figsize=(10,6))
# H0, H1 곡선
plt.plot(x, pdf_H0, label='H0', color='blue')
plt.plot(x, pdf_H1, label='H1', color='red')
# α 영역 (H0 기각)
plt.fill_between(x, 0, pdf_H0, where=(x > z_alpha), color='blue', alpha=0.3, label='α (Type I error)')
# β 영역 (H1인데 H0 채택)
plt.fill_between(x, 0, pdf_H1, where=(x <= z_alpha), color='red', alpha=0.3, label='β (Type II error)')
# 검정력 영역 (1-β)
plt.fill_between(x, 0, pdf_H1, where=(x > z_alpha), color='green', alpha=0.3, label='Power (1-β)')
plt.axvline(z_alpha, color='black', linestyle='--', label='Critical value')
plt.title('Hypothesis Testing: α, β, Power, H0 & H1')
plt.xlabel('Test Statistic')
plt.ylabel('Density')
plt.legend()
plt.show()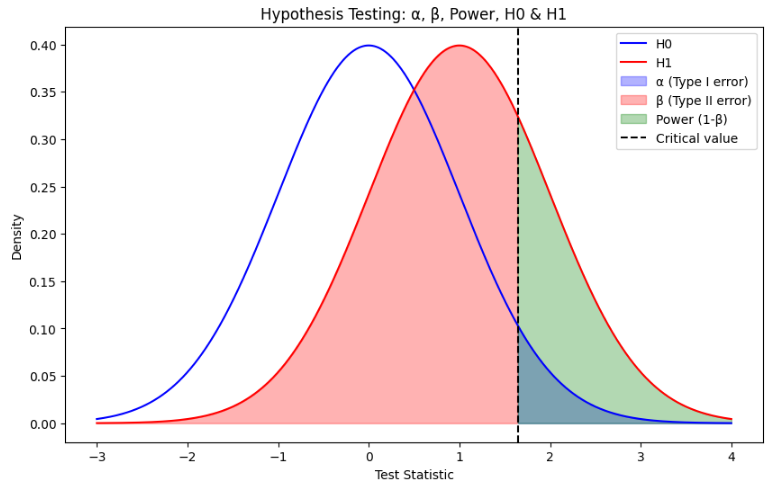
'개발 > Python' 카테고리의 다른 글
| map, apply, transform (0) | 2025.10.25 |
|---|---|
| 라벨 스무딩 (Label Smoothing) (0) | 2025.10.25 |
| 마할라노비스 거리 (0) | 2025.10.25 |
| 로버스트 피팅 (0) | 2025.10.25 |
| 하이퍼 파라미터 튜닝 (0) | 2025.10.25 |
댓글