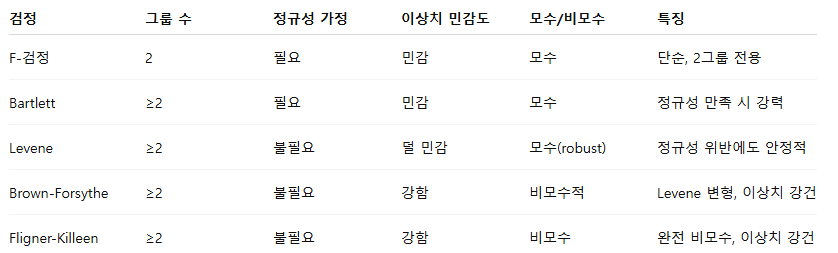
F-검정 (F-test for equality of variances)
- 두 그룹의 분산이 같은지 비교 (모수 검정)
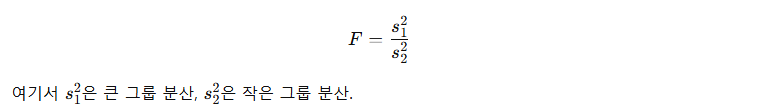
가정
- 각 그룹이 정규분포를 따른다.
- 관측치가 독립이다.
- 비교 대상이 2개 그룹일 때만 적용 가능.
장점
- 계산이 단순하고 이해하기 쉽다.
단점
- 정규성 가정을 크게 따르기 때문에, 비정규 분포에서는 민감하게 반응.
- 그룹이 2개 이상이면 사용 불가.
Bartlett 검정
- 여러 그룹(2개 이상)의 분산이 같은지 검정
- 귀무가설: 모든 그룹의 분산이 동일
- 검정통계량은 Chi-square 근사 사용
- 모수검정
가정
- 각 그룹이 정규분포
- 독립 표본
장점
- 정규성 조건 하에서는 강력(powerful)함
- 2개 이상 그룹에서도 사용 가능
단점
- 정규성 위반에 매우 민감
- 비정규 분포에서는 잘못된 결과를 낼 수 있음
Levene 검정
- 그룹 간 분산 동질성 검정
- 평균 대신 중앙값(median)이나 절대편차 사용 가능 → 정규성 위반에 강함
- 귀무가설 : 모든 그룹 분산 동일
- 모수적이지만 robust (중앙값 기반 사용 시 비모수적 느낌)
가정
- 정규분포 가정 불필요 (robust)
- 독립 표본
장점
- 정규성이 깨져도 강건함
- 2개 이상 그룹 가능
- Bartlett보다 정규성 위반 시 덜 민감
단점
- 정규성일 경우 Bartlett보다 검정력이 약간 낮음
Fligner-Killeen 검정
- 여러 그룹의 분산이 동일한지 검정, 비모수적 접근
- 중앙값 기반, Rank 변환 이용
- 비모수 검정
가정
- 정규성 가정 불필요
- 독립 표본
장점
- 정규성 가정 없이 안정적
- 이상치에 강함
단점
- 계산 복잡도가 Levene보다 약간 높음
Brown-Forsythe 검정
- Levene 검정 변형 (비모수적 검정)
- 중앙값 기준으로 편차 계산 → 정규성, 이상치에 강함
가정
- 정규성 불필요
- 독립 표본
장점
- Levene보다 이상치 강건성 높음
단점
- 약간 복잡
'개발 > Python' 카테고리의 다른 글
| 기본 문법 (0) | 2025.10.25 |
|---|---|
| 데이터 변환 (0) | 2025.10.25 |
| BernoulliNB (나이브 베이즈) (0) | 2025.10.20 |
| 이상치 탐지 vs 특이치 탐지 (0) | 2025.10.20 |
| 합성곱 신경망 (Feature Map) (0) | 2025.10.20 |

댓글