반응형
Box-Cox 변환 (Box-Cox transformation)
- 데이터의 분포를 정규 분포(정규성)에 가깝게 만들기 위해 사용하는 통계적 기법
- 회귀 분석, 분산분석(ANOVA), 시계열 분석 등에서 정규성 가정이 중요한 경우에 사용
목적
- 데이터의 정규성(normality) 확보
- 분산의 안정화(variance stabilization)
- 선형성(linearity) 확보
- 통계 모델의 성능 향상


# λ가 1보다 크면 새로운 분포는 X보다 좌측으로 치우친다.
# 0 <= λ < 1 이라면 우측의 꼬리 영역의 길이가 짧아진다.
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from scipy.stats import skew
# 1. 원래 데이터 생성 (오른쪽으로 치우친 분포)
np.random.seed(0)
X = np.random.normal(loc=0, scale=1.0, size=1000) + 5
# 2. 다양한 lambda 값에 대해 변환
lambdas = [0.01, 1.0, 5.0] # λ < 1, λ = 1, λ > 1
plt.figure(figsize=(12, 6))
for i, lam in enumerate(lambdas, 1):
X_new = X ** lam
sk = skew(X_new)
plt.subplot(1, 3, i)
sns.histplot(X_new, kde=True, bins=30, color='skyblue')
plt.title(f"lambda = {lam}\nSkewness = {sk:.2f}")
plt.xlabel("X^λ")
plt.ylabel("Count")
plt.tight_layout()
plt.show()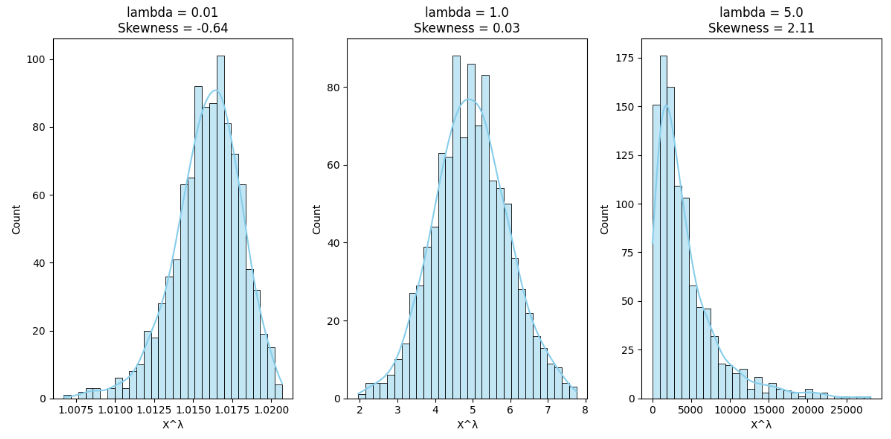
lmbda를 설정하지 않으면 가장 적합한 λ를 반환
import numpy as np
import pandas as pd
np.random.seed(1234)
original_data = np.random.exponential(scale=2.0, size=100)
df = pd.DataFrame({'original': original_data})
from scipy.stats import boxcox
transformed_data, best_lambda = boxcox(df['original'])
df['boxcox'] = transformed_data
import matplotlib.pyplot as plt
import seaborn as sns
fig, axes = plt.subplots(1, 2, figsize=(12, 5))
sns.histplot(df['original'], kde=True, ax=axes[0])
axes[0].set_title('Original Data')
sns.histplot(df['boxcox'], kde=True, ax=axes[1])
axes[1].set_title('Box-Cox Transformed Data')
plt.tight_layout()
plt.show()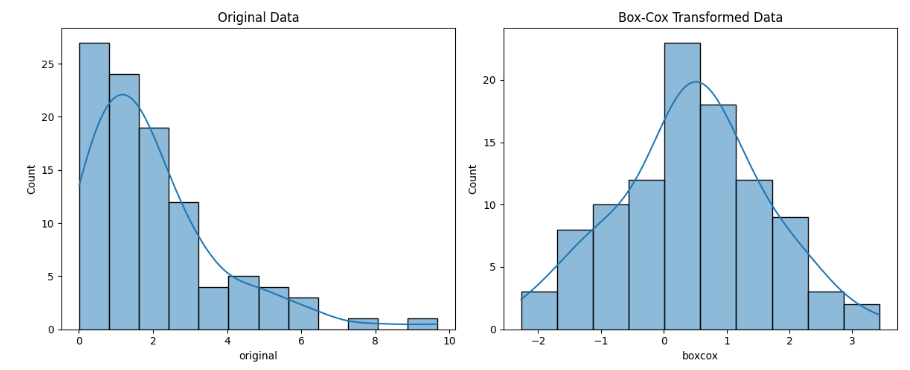
lmbda를 설정하면 해당 값으로 변환
y = boxcox(x, lmbda=0.5) # λ=0.5로 변환
alpha
- lambda 값의 신뢰구간(confidence interval)을 계산할 때 사용
- 1-α 수준으로 신뢰구간을 만든다. ex. alpha=0.05이면 95% 신뢰구간
- lambda_ci : best_lambda 주변에서 Box-Cox 변환의 통계적으로 안정적인 범위
ex. best_lambda=0.3이고 lambda_ci=(0.1, 0.5) → λ를 0.1~0.5 사이로 선택해도 변환 효과가 거의 비슷
from scipy.stats import boxcox
import numpy as np
x = np.array([1, 2, 3, 4, 5])
y, best_lambda, lambda_ci = boxcox(x, alpha=0.05)
print("Best lambda:", best_lambda)
print("95% confidence interval:", lambda_ci)
# Best lambda: 0.6902965863877905
# 95% confidence interval: (-1.104639563718634, 2.74587760733465)Yeo-Johnson 변환(Yeo-Johnson Transformation)
- 데이터의 정규성(Normality) 을 개선하기 위해 사용하는 비선형 스케일링 기법
- 데이터 분포를 정규분포(가우시안 분포)에 가깝게 만들기 위해 사용
목적
- 정규분포와 유사하게 만들기 위해 데이터의 분포를 왜곡을 줄이면서 변형
- 특히 통계 분석, 머신러닝 모델에서 가정된 정규성(normality assumption)을 만족하도록 도와줌
- 양수, 0, 음수 모두에 적용 가능 → Box-Cox 변환의 확장판

import numpy as np
import pandas as pd
np.random.seed(1234)
df = pd.DataFrame({
'skewed_positive': np.random.exponential(scale=2, size=1000), # 오른쪽으로 치우침
'skewed_negative': -np.random.exponential(scale=2, size=1000), # 왼쪽으로 치우침
'normal_like': np.random.normal(loc=0, scale=1, size=1000), # 거의 정규분포
})
from scipy.stats import yeojohnson
df_scipy = df.copy()
result, ld = yeojohnson(df['skewed_positive'])
df_scipy['skewed_positive_yj'] = result
print("lambda :", ld)
result, ld = yeojohnson(df['skewed_negative'])
df_scipy['skewed_negative_yj'] = result
print("lambda :", ld)
result, ld = yeojohnson(df['normal_like'])
df_scipy['normal_like_yj'] = result
print("lambda :", ld)
import matplotlib.pyplot as plt
import seaborn as sns
# 3. 시각화 비교
fig, axes = plt.subplots(3, 2, figsize=(12, 9))
fig.suptitle('Before and After Yeo-Johnson Transformation', fontsize=16)
for i, col in enumerate(['skewed_positive', 'skewed_negative', 'normal_like']):
# Before
sns.histplot(df_scipy[col], bins=30, kde=True, ax=axes[i, 0], color='skyblue')
axes[i, 0].set_title(f'Original: {col}')
# After
sns.histplot(df_scipy[col + '_yj'], bins=30, kde=True, ax=axes[i, 1], color='lightgreen')
axes[i, 1].set_title(f'Transformed: {col}')
plt.tight_layout(rect=[0, 0.03, 1, 0.95])
plt.show()
왼쪽으로 꼬리가 긴 데이터
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from scipy.stats import skew, boxcox
np.random.seed(42)
n = 10000
# 오른쪽 꼬리 (lognormal)
right_skewed = np.random.lognormal(mean=0, sigma=0.8, size=n)
# 왼쪽 꼬리 (반사)
max_val = right_skewed.max() + 5
left_skewed = max_val - right_skewed
df = pd.DataFrame({
'right_skewed': right_skewed,
'left_skewed': left_skewed
})
print("=== Skewness ===")
print(f"Right-skewed: {skew(df['right_skewed']):.3f}")
print(f"Left-skewed : {skew(df['left_skewed']):.3f}\n")
# ==================== 왼쪽 꼬리 변환 비교 ====================
data = df['left_skewed'].copy()
min_val = data.min()
shift = abs(min_val) + 1e-6 if min_val <= 0 else 0
print("왼쪽 꼬리 변환 후 skewness 비교:")
print(f"Original : {skew(data):.3f}")
# 직접 변환
sqrt_direct = np.sqrt(data)
log_direct = np.log(data + shift)
power_direct = data ** 0.3
# Box-Cox (양수 보장 위해 shift)
bc_input = data + shift
bc_direct, _ = boxcox(bc_input)
# 반사 후 변환
reflected = max_val - data
sqrt_reflect = np.sqrt(reflected)
log_reflect = np.log(reflected)
print(f"√x (직접) : {skew(sqrt_direct):.3f}")
print(f"log(x + shift) (직접) : {skew(log_direct):.3f}")
print(f"x^0.3 (직접) : {skew(power_direct):.3f}")
print(f"Box-Cox (직접) : {skew(bc_direct):.3f}")
print(f"Reflect → √x : {skew(sqrt_reflect):.3f}")
print(f"Reflect → log(x) : {skew(log_reflect):.3f}")
# 시각화
plt.figure(figsize=(18, 10))
plt.subplot(2, 4, 1)
sns.histplot(data, kde=True, bins=60, color='salmon')
plt.title('Original\n(Left-skewed)')
plt.subplot(2, 4, 2)
sns.histplot(sqrt_direct, kde=True, bins=60, color='orange')
plt.title('√x')
plt.subplot(2, 4, 3)
sns.histplot(log_direct, kde=True, bins=60, color='green')
plt.title('log(x + shift)')
plt.subplot(2, 4, 4)
sns.histplot(power_direct, kde=True, bins=60, color='purple')
plt.title('x^0.3')
plt.subplot(2, 4, 5)
sns.histplot(bc_direct, kde=True, bins=60, color='red')
plt.title('Box-Cox (shift)')
plt.subplot(2, 4, 6)
sns.histplot(sqrt_reflect, kde=True, bins=60, color='darkorange')
plt.title('Reflect → √x')
plt.subplot(2, 4, 7)
sns.histplot(log_reflect, kde=True, bins=60, color='limegreen')
plt.title('Reflect → log(x)')
plt.subplot(2, 4, 8)
sns.histplot(reflected, kde=True, bins=60, color='gray')
plt.title('Reflected (right)')
plt.tight_layout()
plt.show()
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from scipy.stats import skew, boxcox
# 재현성을 위해 시드 고정
np.random.seed(42)
n = 10000
# 1. 오른쪽 꼬리가 긴 분포 (Right-skewed: lognormal)
right_skewed = np.random.lognormal(mean=0, sigma=0.8, size=n)
# 2. 왼쪽 꼬리가 긴 분포 (Left-skewed: lognormal을 반사)
max_val = right_skewed.max() + 3
left_skewed = max_val - right_skewed
# DataFrame 생성
df = pd.DataFrame({
'right_skewed': right_skewed,
'left_skewed': left_skewed
})
print("=== Skewness 확인 ===")
print(f"Right-skewed skewness: {skew(df['right_skewed']):.3f}")
print(f"Left-skewed skewness: {skew(df['left_skewed']):.3f}")
print("\n기본 통계량:")
print(df.describe())
# ==================== 원본 분포 ====================
plt.figure(figsize=(12, 5))
plt.subplot(1, 2, 1)
sns.histplot(df['right_skewed'], kde=True, bins=60, color='skyblue')
plt.title('(Right-skewed)')
plt.xlabel('value')
plt.subplot(1, 2, 2)
sns.histplot(df['left_skewed'], kde=True, bins=60, color='salmon')
plt.title('(Left-skewed)')
plt.xlabel('value')
plt.tight_layout()
plt.show()
# ==================== 오른쪽 꼬리 변환 예시 ====================
plt.figure(figsize=(16, 10))
data = df['right_skewed']
min_shift = data.min() + 1e-6 # log, boxcox 안전용
plt.subplot(2, 3, 1)
sns.histplot(data, kde=True, bins=60)
plt.title('Original (Right-skewed)')
plt.subplot(2, 3, 2)
sns.histplot(np.sqrt(data), kde=True, bins=60, color='orange')
plt.title('√x (Square Root)')
plt.subplot(2, 3, 3)
sns.histplot(np.log(data), kde=True, bins=60, color='green')
plt.title('log(x) (Natural Log)')
plt.subplot(2, 3, 4)
sns.histplot(data ** 0.3, kde=True, bins=60, color='purple')
plt.title('x^0.3 (Power Transformation)')
plt.subplot(2, 3, 5)
bc, _ = boxcox(data) # Box-Cox (lambda 자동 최적)
sns.histplot(bc, kde=True, bins=60, color='red')
plt.title('Box-Cox Transformation')
plt.subplot(2, 3, 6)
sns.histplot(data ** 2, kde=True, bins=60, color='gray')
plt.title('x² → more skew')
plt.tight_layout()
plt.show()
# ==================== 왼쪽 꼬리 변환 예시 ====================
plt.figure(figsize=(15, 5))
# 반사 (reflect)해서 오른쪽 skew로 만든 후 변환
reflected = max_val - df['left_skewed']
plt.subplot(1, 3, 1)
sns.histplot(df['left_skewed'], kde=True, bins=60, color='salmon')
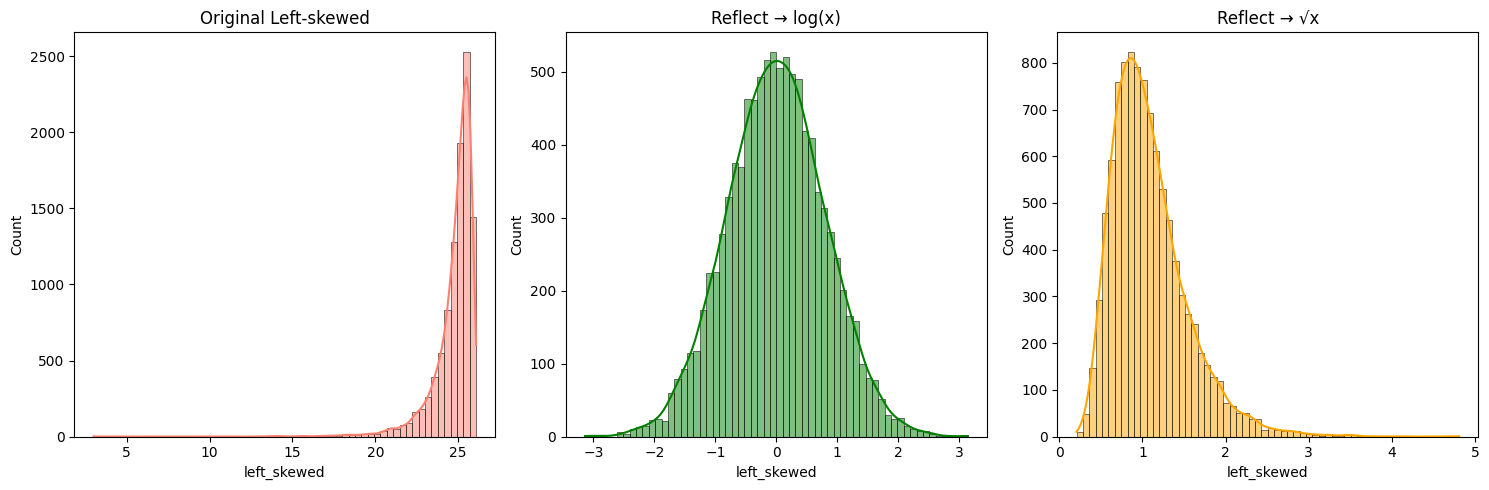
plt.title('Original Left-skewed')
plt.subplot(1, 3, 2)
sns.histplot(np.log(reflected), kde=True, bins=60, color='green')
plt.title('Reflect → log(x)')
plt.subplot(1, 3, 3)
sns.histplot(np.sqrt(reflected), kde=True, bins=60, color='orange')
plt.title('Reflect → √x')
plt.tight_layout()
plt.show()
print("\n✅ 변환 후 skewness 예시 (오른쪽 꼬리)")
print(f"Original : {skew(data):.3f}")
print(f"√x : {skew(np.sqrt(data)):.3f}")
print(f"log(x) : {skew(np.log(data)):.3f}")
print(f"x^0.3 : {skew(data**0.3):.3f}")
print(f"Box-Cox : {skew(bc):.3f}")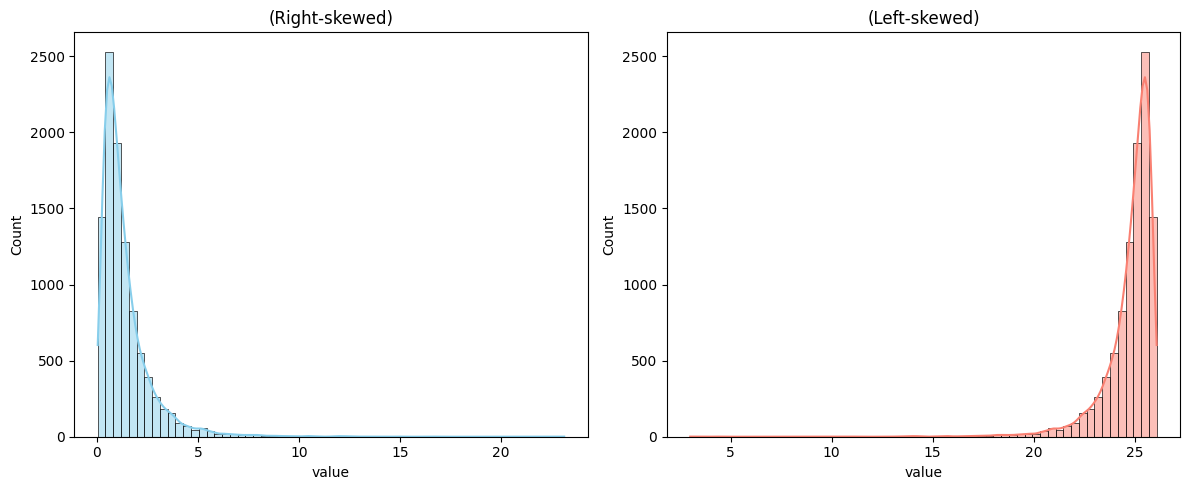

참고
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# 재현 가능하게 시드 고정
np.random.seed(42)
n = 5000 # 샘플 개수
# -----------------------------
# 1) 여러 분포 데이터 생성
# -----------------------------
# 정규분포 (Normal)
normal = np.random.normal(loc=0, scale=1, size=n)
# 오른쪽 꼬리 긴 분포 (Right-skewed)
# 대표적으로 로그정규(Lognormal), 지수(Exponential), 감마(Gamma)
right_lognormal = np.random.lognormal(mean=0, sigma=0.6, size=n)
right_exponential = np.random.exponential(scale=1.0, size=n)
# 왼쪽 꼬리 긴 분포 (Left-skewed)
# 방법 1) 오른쪽 꼬리 분포를 "부호 반전"하면 왼쪽 꼬리가 됨
left_skewed = -np.random.lognormal(mean=0, sigma=0.6, size=n)
# 방법 2) 베타(Beta) 분포를 뒤집어서 왼쪽 꼬리 만들기
# Beta(a,b)에서 a>b면 1쪽에 몰림 → 1 - Beta(...)로 왼쪽 꼬리 느낌
left_beta = 1 - np.random.beta(a=5, b=2, size=n)
# 그 외 유명한 분포들
uniform = np.random.uniform(low=-2, high=2, size=n) # 균등분포
bimodal = np.r_[np.random.normal(-2, 0.6, n//2),
np.random.normal(2, 0.6, n//2)] # 이봉분포(혼합정규)
t_dist = np.random.standard_t(df=3, size=n) # t분포(두꺼운 꼬리)
poisson = np.random.poisson(lam=3, size=n) # 포아송(이산)
gamma = np.random.gamma(shape=2.0, scale=1.0, size=n) # 감마(오른쪽 꼬리)
# -----------------------------
# 2) DataFrame 만들기
# -----------------------------
df = pd.DataFrame({
"normal": normal,
"right_lognormal": right_lognormal,
"right_exponential": right_exponential,
"left_skewed_neg_lognormal": left_skewed,
"left_beta": left_beta,
"uniform": uniform,
"bimodal": bimodal,
"t_dist_df3": t_dist,
"poisson_lam3": poisson,
"gamma_shape2": gamma
})
print(df.head())
print("\n요약통계:\n", df.describe())
# -----------------------------
# 3) 히스토그램 그리기
# -----------------------------
fig, axes = plt.subplots(2, 5, figsize=(18, 7))
axes = axes.ravel()
for i, col in enumerate(df.columns):
ax = axes[i]
ax.hist(df[col], bins=50, density=True, alpha=0.8)
ax.set_title(col)
ax.grid(alpha=0.2)
plt.tight_layout()
plt.show()
반응형
'개발 > Python' 카테고리의 다른 글
| 하이퍼 파라미터 튜닝 (0) | 2025.10.25 |
|---|---|
| 기본 문법 (0) | 2025.10.25 |
| 등분산성 검정 (0) | 2025.10.20 |
| BernoulliNB (나이브 베이즈) (0) | 2025.10.20 |
| 이상치 탐지 vs 특이치 탐지 (0) | 2025.10.20 |
댓글