반응형
선형회귀모델 F-검정 통계량을 구해보자.
회귀제곱합 (SSR)

잔차제곱합 (SSE)

에 대해 검정통계량은 다음과 같다. (n: 예측 데이터의 수, p : 입력 변수의 수)
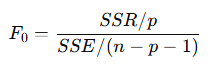

이때 F0는
귀무가설 : 선형회귀모형의 절편을 제외한 모든 회귀 계수는 0이다.
의 검정통계량이 되고, F(p, n - p - 1)분포를 따른다.
F-분포는 0 이상에서만 정의되고, 오른쪽으로 꼬리가 긴 형태이다.
따라서 p-value는 다음과 같이 계산한다.

Fcdf(x)는 누적분포함수로 왼쪽 면적을 구하기 때문에, 오른쪽 꼬리의 면적을 구하려면 1 - Fcdf(F0)로 계산하면 된다.
pval = 1 - f.cdf(F0, p, n-p-1)
절편이 없는 회귀 모형의 경우는 SSR의 자유도가 달라지기 때문에 아래와 같이 공식이 변경된다.

아래 데이터로 위의 내용을 확인해보자.
import pandas as pd
import numpy as np
np.random.seed(1234)
# 100행 × 15개 독립변수 생성
X = pd.DataFrame(
np.random.randn(100, 15),
columns=[f'X{i+1}' for i in range(15)]
)
# 3의 배수 컬럼 선택
cols_3_multiple = [col for col in X.columns if int(col[1:]) % 3 == 0]
# 랜덤 가중치 생성
weights = np.random.uniform(1, 5, size=len(cols_3_multiple))
# 선형 결합으로 y 생성
y = X[cols_3_multiple].dot(weights) + np.random.randn(100) * 0.5 # 약간의 노이즈 추가
# DataFrame 결합
df = X.copy()
df['y'] = y
df
ols에 수식을 넣기 위해 join을 이용하였다.
cols = df.columns.tolist()
cols.remove('y')
X = " + ".join(cols)
X
모델을 학습시키고 fvalue에서 검정통계량 F0를 얻을 수 있다.
from statsmodels.formula.api import ols
model = ols(f"y ~ {X}", df).fit()
model.fvalue # 1640.818370770911
실제 공식에 그대로 대입해도 같은 값이 나온다.
y_true = df['y']
y_pred = model.predict(df)
y_mean = np.mean(y_true)
p = len(cols)
n = len(y_pred)
F0 = (np.sum((y_pred - y_mean)**2)/p) / (np.sum((y_true - y_pred)**2)/(n-p-1))
F0 # 1640.818370770912
그리고 이 검정 통계량이 유의미한지 F 분포를 이용해서 확인할 수 있다.
from scipy.stats import f
pval = 1 - f.cdf(F0, p, n-p-1)
pval # 1.1102230246251565e-16절편이 없는 모형인 경우
ols의 수식에 + 0을 추가하면 fvalue가 다음과 같이 변한다.
from statsmodels.formula.api import ols
model = ols(f"y ~ {X} + 0", df).fit()
model.fvalue # 1734.3598392439164
공식을 다시 수정하면 같은 값이 나오는 것을 알 수 있다.
y_true = df['y']
y_pred = model.predict(df)
y_mean = np.mean(y_true)
# 무절편 모형의 SSR은 'uncentered' => 평균 빼지 않음
SSR = np.sum(y_pred ** 2)
SSE = np.sum((y_true - y_pred) ** 2)
F0 = (SSR / p) / (SSE / (n - p))
F0 # 1734.3598392439153
반응형
'개발 > Python' 카테고리의 다른 글
| Pandas - groupby size vs count (1) | 2025.08.18 |
|---|---|
| 병합적 군집분석 (노드 별 관측치의 수) (1) | 2025.08.17 |
| 이원분산분석 (Two-Way ANOVA) (1) | 2025.08.16 |
| 결정 트리 (부스팅) (3) | 2025.08.15 |
| statsmodels ols 결과 출력하기 (1) | 2025.08.15 |




댓글