유니티 - 2차원 평면에서 유한한 선의 교점 구하기 (Intersection of Two Finite Lines in 2-Dimension)

Unity 전체 링크

 

2차원 평면 (y = 0)에서 길이가 정해진 두 개의 선의 교차점을 구해보자.

 

점 (x1, y1)과 점 (x2, y2)를 지나는 직선과 점 (x3, y3)와 점 (x4, y4)를 지나는 직선이 있을 때,

Cross를 다음과 같이 정의하자.

 

 

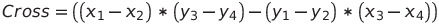
Cross가 0인 경우는 두 직선이 평행(parallel)한 경우다.

 

그리고 Cross가 0이 아니라면 두 직선의 교점 (X, Y)는 다음과 같다.

 

 

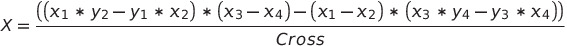
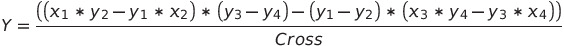
따라서 교차하는지 검사하는 함수는 다음과 같다. (y = 0인 공간이므로 y → z로 변경)

    bool CrossCheck2D(Vector3 a, Vector3 b, Vector3 c, Vector3 d)
    {
        // (x, 0, z)
        float x1, x2, x3, x4, z1, z2, z3, z4, X, Z;

        x1 = a.x; z1 = a.z;
        x2 = b.x; z2 = b.z;
        x3 = c.x; z3 = c.z;
        x4 = d.x; z4 = d.z;

        float cross = ((x1 - x2) * (z3 - z4) - (z1 - z2) * (x3 - x4));

        if (cross == 0 /* parallel */) return false;
        else return true;
    }

 

교점의 좌표를 구하는 함수는 다음과 같다. 

cross가 0인 경우 적절한 예외처리가 필요하다.

    Vector3 CrossCheck2DVector(Vector3 a, Vector3 b, Vector3 c, Vector3 d)
    {
        // (x, 0, z)
        float x1, x2, x3, x4, z1, z2, z3, z4, X, Z;

        x1 = a.x; z1 = a.z;
        x2 = b.x; z2 = b.z;
        x3 = c.x; z3 = c.z;
        x4 = d.x; z4 = d.z;

        float cross = ((x1 - x2) * (z3 - z4) - (z1 - z2) * (x3 - x4));
        if (cross == 0 /* parallel */) return new Vector3(10000, 10000, 10000);

        X = ((x1 * z2 - z1 * x2) * (x3 - x4) - (x1 - x2) * (x3 * z4 - z3 * x4)) / cross;
        Z = ((x1 * z2 - z1 * x2) * (z3 - z4) - (z1 - z2) * (x3 * z4 - z3 * x4)) / cross;

        return new Vector3(X, 0, Z);
    }

---

이제 게임 오브젝트를 4개 추가하여 직선 2개를 만들고, 교차점에 큐브가 보이도록 해보자.

각각의 직선을 사용하기 위해 라인 렌더러를 추가한다.

using System.Collections;
using System.Collections.Generic;
using UnityEngine;

public class CheckCrossFiniteLine : MonoBehaviour
{
    public GameObject go1, go2, go3, go4, cube;
    public LineRenderer lr1, lr2;

    bool CrossCheck2D(Vector3 a, Vector3 b, Vector3 c, Vector3 d)
    {
        // (x, 0, z)
        float x1, x2, x3, x4, z1, z2, z3, z4, X, Z;

        x1 = a.x; z1 = a.z;
        x2 = b.x; z2 = b.z;
        x3 = c.x; z3 = c.z;
        x4 = d.x; z4 = d.z;

        float cross = ((x1 - x2) * (z3 - z4) - (z1 - z2) * (x3 - x4));

        if (cross == 0 /* parallel */) return false;
        else return true;
    }

    Vector3 CrossCheck2DVector(Vector3 a, Vector3 b, Vector3 c, Vector3 d)
    {
        // (x, 0, z)
        float x1, x2, x3, x4, z1, z2, z3, z4, X, Z;

        x1 = a.x; z1 = a.z;
        x2 = b.x; z2 = b.z;
        x3 = c.x; z3 = c.z;
        x4 = d.x; z4 = d.z;

        float cross = ((x1 - x2) * (z3 - z4) - (z1 - z2) * (x3 - x4));
        if (cross == 0 /* parallel */) return new Vector3(10000, 10000, 10000);

        X = ((x1 * z2 - z1 * x2) * (x3 - x4) - (x1 - x2) * (x3 * z4 - z3 * x4)) / cross;
        Z = ((x1 * z2 - z1 * x2) * (z3 - z4) - (z1 - z2) * (x3 * z4 - z3 * x4)) / cross;

        return new Vector3(X, 0, Z);
    }

    void Start()
    {
        lr1.startWidth = lr1.endWidth = .1f;
        lr1.material.color = Color.blue;

        lr2.startWidth = lr2.endWidth = .1f;
        lr2.material.color = Color.red;

        lr1.positionCount = lr2.positionCount = 2;
    }

    void Update()
    {
        Vector3 pos1, pos2, pos3, pos4;

        pos1 = go1.transform.position;
        pos2 = go2.transform.position;
        pos3 = go3.transform.position;
        pos4 = go4.transform.position;

        lr1.SetPosition(0, pos1);
        lr1.SetPosition(1, pos2);
                           
        lr2.SetPosition(0, pos3);
        lr2.SetPosition(1, pos4);

        if(CrossCheck2D(pos1, pos2, pos3, pos4))
        {
            cube.transform.position = CrossCheck2DVector(pos1, pos2, pos3, pos4);
        }
        else
        {
            cube.transform.position = new Vector3(0, 10000, 0);
        }
    }
}

 

빈 오브젝트에 라인 렌더러를 추가한다. (x 2개)

 

그리고 빈 오브젝트를 하나 더 생성해서 CheckCrossFiniteLine.cs를 추가하고 오브젝트를 할당한다.

 

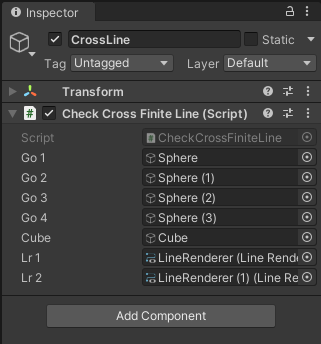
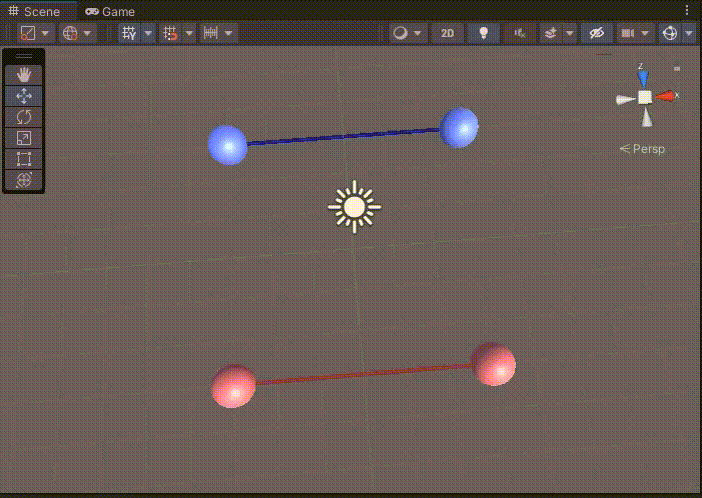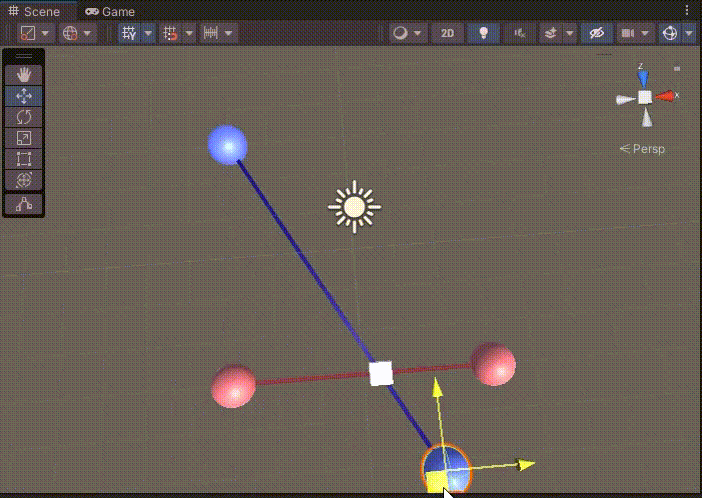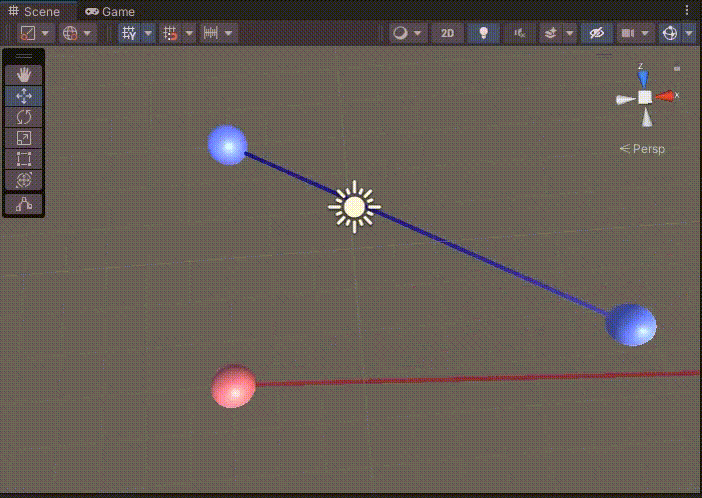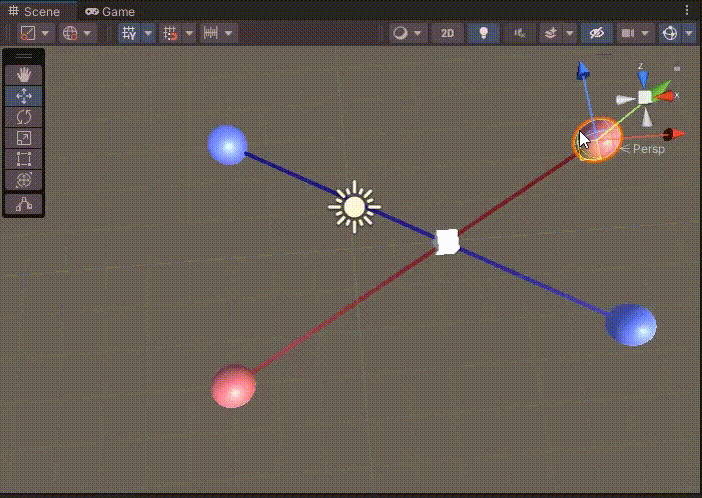
아래와 같이 오브젝트를 배치하였다. 

게임을 실행하면 파란 공은 파란 공끼리, 빨간 공은 빨간 공끼리 연결된다.

 

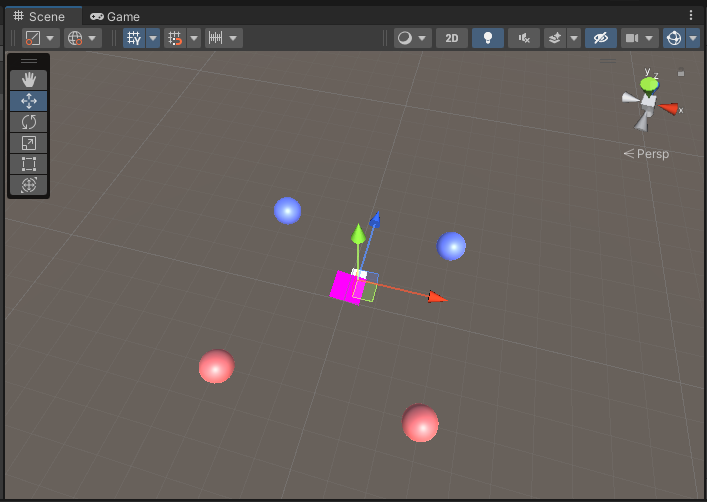
게임을 실행한 후 Scene에서 직선을 변경해보자. (y = 0 고정)

 

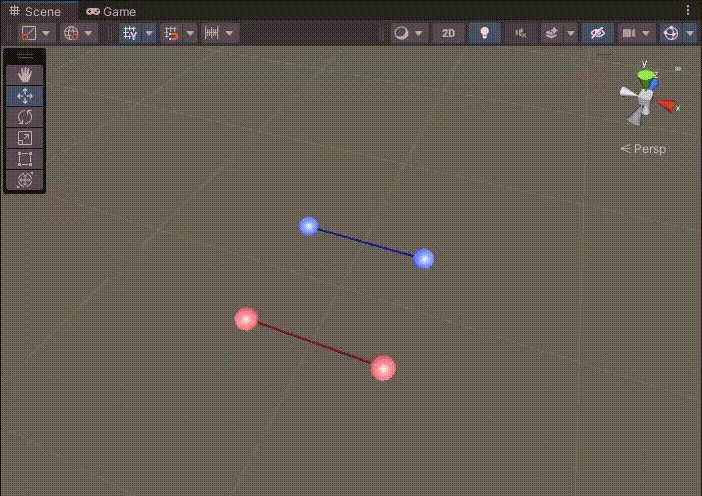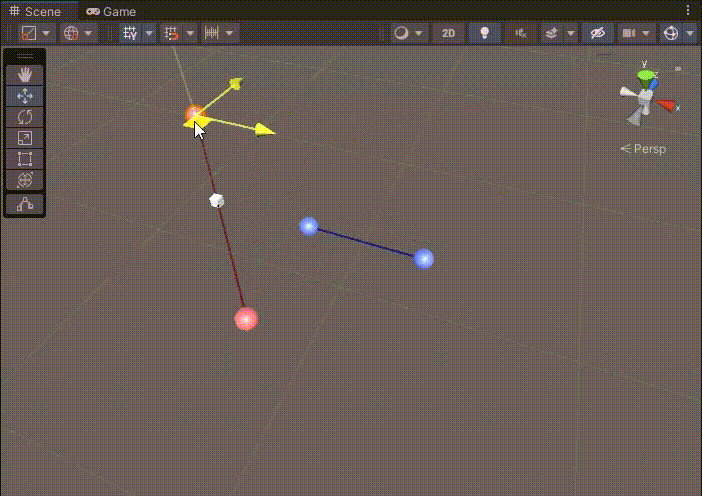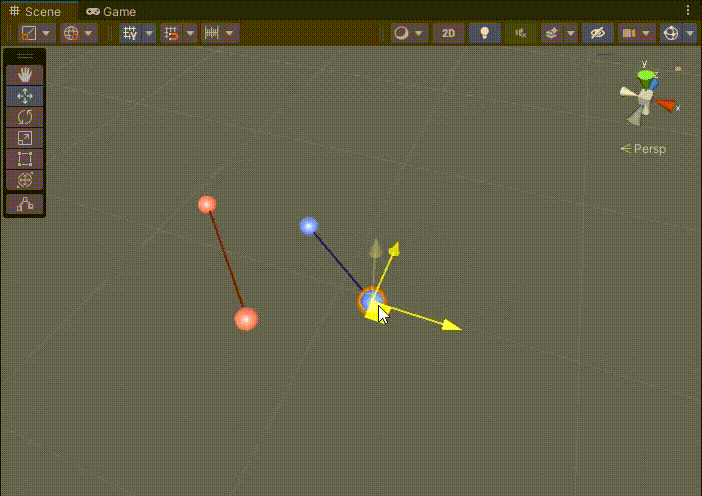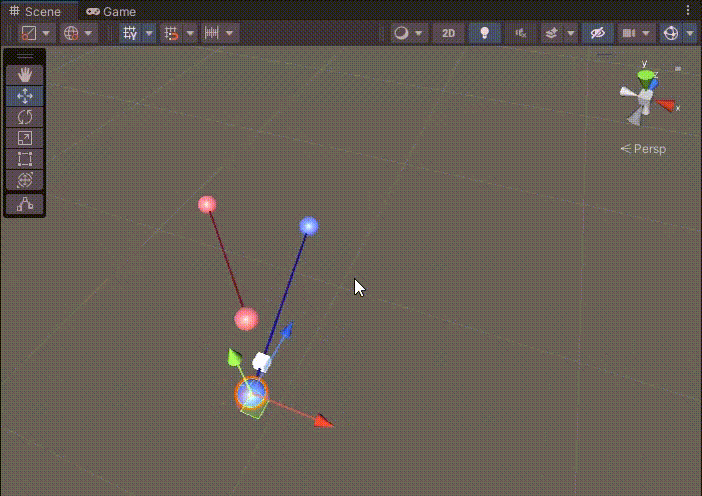
두 직선의 교점 (X, Y) 공식은 직선이 무한한 것을 가정한 공식이다.

따라서 두 직선이 겹치지 않아도 연장선에 큐브가 생성되었다.

 

유한한 직선 내에만 교점이 생성되는지 확인하려면 교점의 좌표가 각 직선 내부에 있는지 검사할 필요가 있다.

두 점 (A, B)가 직선이고 내부에 교점 D가 있다면

A - D - B가 되므로 선분 AB의 길이 = 선분 AD + 선분 DA를 만족해야한다.

D가 외부에 있다면 선분 AB의 길이 < 선분 AD + 선분 DA 가 된다. (소수점 연산이므로 오차 허용)

    bool CheckDotInLine(Vector3 a, Vector3 b, Vector3 dot)
    {
        float epsilon = 0.00001f;
        float dAB = Vector3.Distance(a, b);
        float dADot = Vector3.Distance(a, dot);
        float dBDot = Vector3.Distance(b, dot);

        return ((dAB + epsilon) >= (dADot + dBDot));
    }

 

CrossCheck2D에서 두 직선이 평행이 아닌 경우, 교점 (X, Z)가 각 선분에 포함되는지 검사하는 코드를 추가한다.

    bool CrossCheck2D(Vector3 a, Vector3 b, Vector3 c, Vector3 d)
    {
        // (x, 0, z)
        float x1, x2, x3, x4, z1, z2, z3, z4, X, Z;

        x1 = a.x; z1 = a.z;
        x2 = b.x; z2 = b.z;
        x3 = c.x; z3 = c.z;
        x4 = d.x; z4 = d.z;

        float cross = ((x1 - x2) * (z3 - z4) - (z1 - z2) * (x3 - x4));

        if (cross == 0 /* parallel */) return false;

        X = ((x1 * z2 - z1 * x2) * (x3 - x4) - (x1 - x2) * (x3 * z4 - z3 * x4)) / cross;
        Z = ((x1 * z2 - z1 * x2) * (z3 - z4) - (z1 - z2) * (x3 * z4 - z3 * x4)) / cross;

        return 
            CheckDotInLine(a, b, new Vector3(X, 0, Z)) 
            && CheckDotInLine(c, d, new Vector3(X, 0, Z));
    }

 

다시 게임을 실행해보자.

이제 길이가 제한된 선분이 직접 겹칠때만 큐브가 만들어진다.

 

최종 코드는 다음과 같다.

using System.Collections;
using System.Collections.Generic;
using UnityEngine;

public class CheckCrossFiniteLine : MonoBehaviour
{
    public GameObject go1, go2, go3, go4, cube;
    public LineRenderer lr1, lr2;

    bool CheckDotInLine(Vector3 a, Vector3 b, Vector3 dot)
    {
        float epsilon = 0.00001f;
        float dAB = Vector3.Distance(a, b);
        float dADot = Vector3.Distance(a, dot);
        float dBDot = Vector3.Distance(b, dot);

        return ((dAB + epsilon) >= (dADot + dBDot));
    }

    bool CrossCheck2D(Vector3 a, Vector3 b, Vector3 c, Vector3 d)
    {
        // (x, 0, z)
        float x1, x2, x3, x4, z1, z2, z3, z4, X, Z;

        x1 = a.x; z1 = a.z;
        x2 = b.x; z2 = b.z;
        x3 = c.x; z3 = c.z;
        x4 = d.x; z4 = d.z;

        float cross = ((x1 - x2) * (z3 - z4) - (z1 - z2) * (x3 - x4));

        if (cross == 0 /* parallel */) return false;

        X = ((x1 * z2 - z1 * x2) * (x3 - x4) - (x1 - x2) * (x3 * z4 - z3 * x4)) / cross;
        Z = ((x1 * z2 - z1 * x2) * (z3 - z4) - (z1 - z2) * (x3 * z4 - z3 * x4)) / cross;

        return 
            CheckDotInLine(a, b, new Vector3(X, 0, Z)) 
            && CheckDotInLine(c, d, new Vector3(X, 0, Z));
    }

    Vector3 CrossCheck2DVector(Vector3 a, Vector3 b, Vector3 c, Vector3 d)
    {
        // (x, 0, z)
        float x1, x2, x3, x4, z1, z2, z3, z4, X, Z;

        x1 = a.x; z1 = a.z;
        x2 = b.x; z2 = b.z;
        x3 = c.x; z3 = c.z;
        x4 = d.x; z4 = d.z;

        float cross = ((x1 - x2) * (z3 - z4) - (z1 - z2) * (x3 - x4));
        if (cross == 0 /* parallel */) return new Vector3(10000, 10000, 10000);

        X = ((x1 * z2 - z1 * x2) * (x3 - x4) - (x1 - x2) * (x3 * z4 - z3 * x4)) / cross;
        Z = ((x1 * z2 - z1 * x2) * (z3 - z4) - (z1 - z2) * (x3 * z4 - z3 * x4)) / cross;

        return new Vector3(X, 0, Z);
    }

    void Start()
    {
        lr1.startWidth = lr1.endWidth = .1f;
        lr1.material.color = Color.blue;

        lr2.startWidth = lr2.endWidth = .1f;
        lr2.material.color = Color.red;

        lr1.positionCount = lr2.positionCount = 2;
    }

    void Update()
    {
        Vector3 pos1, pos2, pos3, pos4;

        pos1 = go1.transform.position;
        pos2 = go2.transform.position;
        pos3 = go3.transform.position;
        pos4 = go4.transform.position;

        lr1.SetPosition(0, pos1);
        lr1.SetPosition(1, pos2);
                           
        lr2.SetPosition(0, pos3);
        lr2.SetPosition(1, pos4);

        if(CrossCheck2D(pos1, pos2, pos3, pos4))
        {
            cube.transform.position = CrossCheck2DVector(pos1, pos2, pos3, pos4);
        }
        else
        {
            cube.transform.position = new Vector3(0, 10000, 0);
        }
    }
}

 

위의 실행결과는 아래의 unitypackage에서 확인 가능하다.

CrossLineCheck.unitypackage

0.03MB

---

수식을 입력하는 링크는 아래를 참고하자.

http://www.sciweavers.org/free-online-latex-equation-editor

 

Cross =  \big(  \big(x_{1} -  x_{2}\big)  * \big(y_{3} -  y_{4}\big) - \big(y_{1} - y_{2}\big)  * \big(x_{3} -  x_{4}\big) \big) 

X =   \frac{\big(  \big(x_{1} * y_{2} -  y_{1} * x_{2}\big)  * \big(x_{3} -  x_{4}\big) - \big(x_{1} - x_{2}\big)  * \big(x_{3} * y_{4} -  y_{3} * x_{4}\big) \big) }{Cross} 

Y =   \frac{\big(  \big(x_{1} * y_{2} -  y_{1} * x_{2}\big)  * \big(y_{3} -  y_{4}\big) - \big(y_{1} - y_{2}\big)  * \big(x_{3} * y_{4} -  y_{3} * x_{4}\big) \big) }{Cross} 

 

Unity Plus:

Easy 2D, 3D, VR, & AR software for cross-platform development of games and mobile apps. - Unity Store

 

Unity Pro:

Unity Pro

 

Unity 프리미엄 학습:

Unity Learn