참고
1차원 배열은 연속된 메모리의 집합이다.
2차원 배열은 [row][col]로 접근하지만, 1차원 배열과 마찬가지로 연속된 메모리의 집합이다.
Cache Friendly Code
- 특정 데이터를 참조할 때, 그 데이터 주위의 데이터도 함께 캐시에 로드되는 특성. (Locality)
- 연속적인 메모리 주소에 있는 데이터는 캐시에 함께 로드될 가능성이 높음.
즉, 2차원 배열(arr[r][c])을 접근할 때, r이 증가하는 방향보다, c가 증가하는 방향으로 먼저 탐색하는 것이 더 빠르다.
임의의 2차원 배열을 만들어서 주소를 출력해보자.
#include <stdio.h>
int main()
{
char arr[5][5];
for (int r = 0; r < 5; r++)
{
for (int c = 0; c < 5; c++)
printf("%x ", &arr[r][c]);
putchar('\n');
}
return 0;
}
char 타입 배열이므로, col이 커질수록 메모리의 주소가 1 단위로 증가하는 것을 알 수 있다.
row가 증가하는 방향은 메모리가 5 단위로 증가한다.

캐시 미스(Cache Miss)는 데이터가 캐시에 없어서 메인 메모리에서 데이터를 가져와야할 때 발생한다.
즉, 연속된 메모리는 쉽게 접근하지만, 비연속적인 메모리는 캐시 미스가 발생하여 속도가 느려진다.
→ Cache Friendly Code에 따라 연속된 메모리로 접근하는 코드가 더 성능이 좋다.
2차원 배열 탐색 속도 비교
2차원 배열 myMap이 있다고 가정하자.
#define MAX (10000)
char myMap[MAX][MAX];
그리고 2개의 함수가 있다.
search1은 row을 기준으로 column을 탐색하고, search2는 column을 기준으로 row를 탐색한다.
여기서는 단순히 배열의 값을 sum에 모두 더하기만 한다.
void search1(char map[MAX][MAX])
{
int sum = 0;
for (int r = 0; r < MAX; r++)
for (int c = 0; c < MAX; c++)
sum += map[r][c];
}
void search2(char map[MAX][MAX])
{
int sum = 0;
for (int c = 0; c < MAX; c++)
for (int r = 0; r < MAX; r++)
sum += map[r][c];
}
탐색 방향만 다를 뿐 두 함수의 결과는 같다.
하지만 함수의 실행속도는 search1이 훨씬 더 빠르다.
아래 코드를 실행해보자.
#include <stdio.h>
#include <time.h>
#define MAX (10000)
char myMap[MAX][MAX];
void search1(char map[MAX][MAX])
{
int sum = 0;
for (int r = 0; r < MAX; r++)
for (int c = 0; c < MAX; c++)
sum += map[r][c];
}
void search2(char map[MAX][MAX])
{
int sum = 0;
for (int c = 0; c < MAX; c++)
for (int r = 0; r < MAX; r++)
sum += map[r][c];
}
int main()
{
int TESTCASE = 10;
{
int TIME = 0;
/* Timer on */
clock_t start = clock();
/* 실행 코드 */
for (int tc = 1; tc <= TESTCASE; tc++)
{
search1(myMap);
}
/* Timer off */
TIME += ((int)clock() - start) / (CLOCKS_PER_SEC / 1000);
printf("\nSEARCH 1 TIME : %d ms\n", TIME); /* ms 단위로 출력 */
}
{
int TIME = 0;
/* Timer on */
clock_t start = clock();
/* 실행 코드 */
for (int tc = 1; tc <= TESTCASE; tc++)
{
search2(myMap);
}
/* Timer off */
TIME += ((int)clock() - start) / (CLOCKS_PER_SEC / 1000);
printf("SEARCH 2 TIME : %d ms\n", TIME); /* ms 단위로 출력 */
}
return 0;
}
search2는 비연속적인 메모리에 접근하기 때문에 연속된 메모리에 접근하는 search1보다 2배 이상 시간이 소모된다.
이런 경우, map을 transpose하고 함수를 사용하는 것이 효율적이다.
void transpose(char map[MAX][MAX])
{
for (int r = 0; r < MAX; r++)
{
for (int c = 0; c < r; c++)
{
int t = map[r][c];
map[r][c] = map[c][r];
map[c][r] = t;
}
}
}
배열을 transpose하고 search1을 사용하면 search2의 순서대로 배열에 접근하게 된다.
transpose + search1 테스트케이스를 추가한 코드를 실행해보자.
#include <stdio.h>
#include <time.h>
#define MAX (10000)
char myMap[MAX][MAX];
void search1(char map[MAX][MAX])
{
int sum = 0;
for (int r = 0; r < MAX; r++)
for (int c = 0; c < MAX; c++)
sum += map[r][c];
}
void search2(char map[MAX][MAX])
{
int sum = 0;
for (int c = 0; c < MAX; c++)
for (int r = 0; r < MAX; r++)
sum += map[r][c];
}
void transpose(char map[MAX][MAX])
{
for (int r = 0; r < MAX; r++)
{
for (int c = 0; c < r; c++)
{
int t = map[r][c];
map[r][c] = map[c][r];
map[c][r] = t;
}
}
}
int main()
{
int TESTCASE = 10;
{
int TIME = 0;
/* Timer on */
clock_t start = clock();
/* 실행 코드 */
for (int tc = 1; tc <= TESTCASE; tc++)
{
search1(myMap);
}
/* Timer off */
TIME += ((int)clock() - start) / (CLOCKS_PER_SEC / 1000);
printf("\nSEARCH 1 TIME : %d ms\n", TIME); /* ms 단위로 출력 */
}
{
int TIME = 0;
/* Timer on */
clock_t start = clock();
/* 실행 코드 */
for (int tc = 1; tc <= TESTCASE; tc++)
{
search2(myMap);
}
/* Timer off */
TIME += ((int)clock() - start) / (CLOCKS_PER_SEC / 1000);
printf("SEARCH 2 TIME : %d ms\n", TIME); /* ms 단위로 출력 */
}
{ // transpose + search1
int TIME = 0;
/* Timer on */
clock_t start = clock();
/* 실행 코드 */
transpose(myMap);
for (int tc = 1; tc <= TESTCASE; tc++)
{
search1(myMap);
}
/* Timer off */
TIME += ((int)clock() - start) / (CLOCKS_PER_SEC / 1000);
printf("SEARCH Transpos + 1 TIME : %d ms\n", TIME); /* ms 단위로 출력 */
}
return 0;
}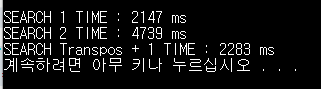
transpose 비용이 발생하지만, 훨씬 더 효율적으로 2차원 배열을 순회하였다.
예시 함수는 단순히 sum에 배열의 값을 더하는 것이므로, 어떤 방향으로 탐색해도 결과가 같았다.
만약, 2차원 배열을 반드시 row 방향으로 탐색해야 한다면, transpose로 배열을 바꾸는 것이 더 효율적일 수 있다.
'알고리즘 > [EXP] 삼성 SW 역량 테스트 C형' 카테고리의 다른 글
| BOJ 5397 : 키로거 with 세그먼트 트리, 링크드 리스트 (0) | 2023.08.25 |
|---|---|
| 세그먼트 트리를 이용한 링크드 리스트의 삽입과 삭제 (1) | 2023.08.25 |
| 타입 캐스팅으로 한 번에 메모리 쓰기, 읽기 (Memory Write and Read with Type Casting) (0) | 2023.08.15 |
| 타입 캐스팅으로 deep copy, memcpy 구현하기 (Memory Copy with Type Casting) (0) | 2023.08.15 |
| 간단한 윤곽선 검출로 정사각형 찾기 (Find Squares with Simple Edge Detection) (0) | 2023.08.14 |




댓글