참고
- 구간 합 구하기 with 바텀 업 세그먼트 트리 (Bottom-Up Segment Tree)
- BOJ 1655 : 가운데를 말해요 with 세그먼트 트리
- BOJ 5397 : 키로거 with 세그먼트 트리, 링크드 리스트 (구현)
append, insert, erase 구현
세그먼트 트리를 이용해 링크드 리스트를 더 빠르게 insert, erase 할 수 있다.
append는 세그먼트 트리에서 node를 순서대로 추가한다.
그리고 insert, erase는 해당 node를 각각 링크드 리스트로 구현하여 해결할 수 있다.
세그먼트 트리의 index를 잘 관리한다면 O(logN) 연산으로 append, insert, erase를 처리할 수 있다.
실제 구현은 BOJ 5397 : 키로거 with 세그먼트 트리, 링크드 리스트를 참고하자.
append
아래와 같이 세그먼트 트리가 있다고 하자.
그리고 각 노드는 링크드 리스트의 Head가 된다.

만약 문자 a를 입력받으면(append) 아래와 같이 트리가 변경된다.

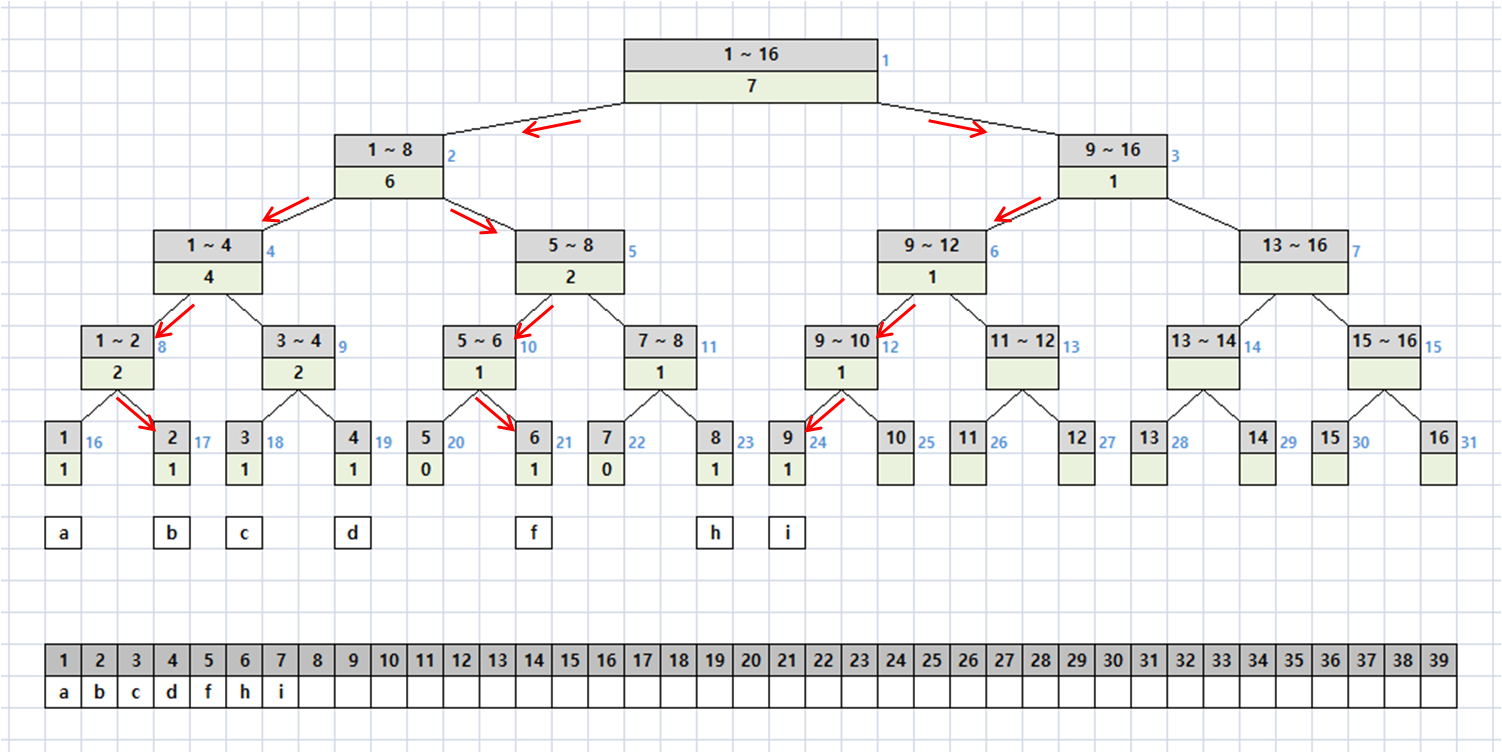
append b ~ i 를 실행하면 트리가 아래와 같이 변하게 된다.

index 관리
항상 append로만 문자가 입력된다면, 세그먼트 트리 대신 링크드 리스트를 사용하면 된다.
하지만 이미 입력된 문자 사이에 다른 문자를 입력하고 싶은 경우,
세그먼트 트리의 가장 아래의 노드를 각각 링크드 리스트로 만들면 삽입, 삭제가 O(logN)만에 가능해진다.
예를 들어 e 앞에 j를 insert 하면 아래와 같이 다섯 번째 노드가 변경된다.

위와 같은 내용을 구현하려면 세그먼트 트리와 각 노드의 링크드 리스트의 index를 잘 관리해야 한다.
세그먼트 트리를 이용한 index 관리는 BOJ 1655 : 가운데를 말해요 with 세그먼트 트리에서 사용한 방법과 동일하다.
여기서 노드의 5번째(= e)가 있는 tree의 index와 해당 node의 index를 구해보자. (j 삽입 전)
노드의 5번째는 e이므로 tree의 index는 15 + 5 = 20이고,
20 - 15, 5번째 node( = 링크드 리스트)에서 e는 첫 번째에 존재하게 된다.
최초 nodeIdx = 5, treeIdx = 1로 시작해 보자.
tree[1 << 1] = 8, idx = 5 이기 때문에 5 <= 8을 만족한다.
: treeIdx <<= 1에 의해 treeIdx = 2, idx = 5 가 된다. (왼쪽 노드로 이동)
tree[2 << 1] = 4, idx = 5 이므로, 5 <= 4를 만족하지 않는다.
: treeIdx <<= 1, ++에 의해 treeIdx = 5가 되고, idx = 1 이 된다. (오른쪽 노드로 이동)
tree[5 << 1] = 2, idx = 1 이고, 1 <= 2를 만족한다.
: treeIdx <<= 1에 의해 treeIdx = 10이 되고, idx = 1 이 된다. (왼쪽 노드로 이동)
tree[10 << 1] = 1, idx = 1 이므로 1 <= 1을 만족한다.
: treeIdx <<= 1에 의해 treeIdx = 20, idx = 1 이 된다. (왼쪽 노드로 이동)
코드로 구현하면 다음과 같다.
void test(int index)
{
int treeIdx = 1;
while (treeIdx < leafSize)
{
if (index <= tree[treeIdx << 1]) treeIdx <<= 1;
else
{
index -= tree[treeIdx << 1];
treeIdx <<= 1;
treeIdx++;
}
}
...
}
위 내용을 그림으로 보면 다음과 같다.

즉, 세그먼트 트리( = 인덱스 트리)로 O(logN)번 만에 append 구현이 가능하다.
insert
삽입을 해도 index가 유지되는지 확인해 보자.
e(5 번째 배열)의 앞에 j를 삽입하면 세그먼트 트리의 5번째 노드의 값은 2가 된다.
그리고 5번째 노드의 링크드 리스트 앞에 j가 추가된다.

이제 전체 문자열 중 5번째 값인 j를 찾을 수 있는지 확인해보자.
nodeIdx = 5, treeIdx = 1로 시작해 보자.
tree[1 << 1] = 9, idx = 5 이기 때문에 5 <= 9을 만족한다.
: treeIdx <<= 1에 의해 treeIdx = 2, idx = 5 가 된다. (왼쪽 노드로 이동)
tree[2 << 1] = 4, idx = 5 이므로, 5 <= 4를 만족하지 않는다.
: treeIdx <<= 1, ++에 의해 treeIdx = 5가 되고, idx = 1 이 된다. (오른쪽 노드로 이동)
tree[5 << 1] = 3, idx = 1 이고, 1 <= 3를 만족한다.
: treeIdx <<= 1에 의해 10이 된다., idx = 1 이 된다. (왼쪽 노드로 이동)
tree[10 << 1] = 2, idx = 1 이므로, 1 <= 2를 만족한다.
: treeIdx <<= 1에 의해 treeIdx = 20, idx = 1 이 된다. (왼쪽 노드로 이동)
따라서 20 - 15 = 5번째 node에 idx = 첫 번째에 j가 존재한다.
그리고 e는 j가 삽입됨에 따라 6번째에 존재하게 될 것이다.
nodeIdx = 6, treeIdx = 1로 시작해 보자.
tree[1 << 1] = 9, idx = 6 이기 때문에 6 <= 9을 만족한다.
: treeIdx <<= 1에 의해 treeIdx = 2, idx = 6 가 된다. (왼쪽 노드로 이동)
tree[2 << 1] = 4, idx = 6 이므로 6 <= 4를 만족하지 않는다.
: treeIdx <<= 1, ++에 의해 treeIdx = 5가 되고, idx = 2 가 된다. (오른쪽 노드로 이동)
tree[5 << 1] = 3, idx = 1 이고 2 <= 3를 만족한다.
: treeIdx <<= 1에 의해 treeIdx = 10이 된다., idx = 2 가 된다. (왼쪽 노드로 이동)
tree[10 << 1] = 2, idx = 2 이므로 2 <= 2를 만족한다.
: treeIdx <<= 1에 의해 treeIdx = 20, idx = 2 이 된다. (왼쪽 노드로 이동)
즉, 20 - 15 = 5번째 node의 두 번째에 e가 존재하므로 전체 순서를 여전히 찾을 수 있다.

이번에도 e 앞에 k를 삽입해서 검증해보자.
j와 e 사이에는 링크드 리스트이므로 O(logN)으로 노드를 이동한 후, O(N)으로 idx = 2 번째까지 k를 삽입한다.
그리고 node의 값은 2 → 3이 된다.

nodeidx = 6, treeIdx = 1로 시작해서 k를 찾을 수 있는지 확인해보자.
tree[1 << 1] = 10, idx = 6 이기 때문에 6 <= 10을 만족한다.
: treeIdx <<= 1에 의해 treeIdx = 2, idx = 6 가 된다. (왼쪽 노드로 이동)
tree[2 << 1] = 4, idx = 6 이고, 6 <= 4를 만족하지 않는다.
: treeIdx <<= 1, ++에 의해 treeIdx = 5가 되고, idx = 2 이 된다. (오른쪽 노드로 이동)
tree[5 << 1] =43, idx = 2 이고 2 <= 4를 만족한다.
: treeIdx <<= 1에 의해 treeIdx = 10이 된다., idx = 2 가 된다. (왼쪽 노드로 이동)
tree[10 << 1] = 3, idx = 2 이므로 2 <= 3를 만족한다.
: treeIdx <<= 1에 의해 treeIdx = 20, idx = 2 가 된다. (왼쪽 노드로 이동)
즉, 20 - 15 = 5번째 node의 두 번째 = k가 된다.

erase
삭제을 해도 index가 유지되는지 확인해보자.
9번째에 있는 g를 삭제해보자.
nodeIdx = 9, treeIdx = 1로 시작해서 g를 찾아보자.
tree[1 << 1] = 10, idx = 9 이기 때문에 9 <= 10을 만족한다.
: treeIdx <<= 1에 의해 treeIdx = 2, idx = 9 가 된다. (왼쪽 노드로 이동)
tree[2 << 1] = 4, idx = 9 가 되고, 9 <= 4를 만족하지 않는다.
: treeIdx <<= 1, ++에 의해 treeIdx = 5가 되고, idx = 5 가 된다. (오른쪽 노드로 이동)
tree[5 << 1] = 4, idx = 5이고, 5 <= 4를 만족하지 않는다.
: treeIdx <<= 1, ++에 의해 treeIdx = 11이 된다., idx = 1 이 된다. (오른쪽 노드로 이동)
tree[11 << 1] = 1, idx = 2 이므로 1 <= 2를 만족한다.
: treeIdx <<= 1에 의해 treeIdx = 22, idx = 1 이 된다. (왼쪽 노드로 이동)
즉, 22 - 15 = 7번째 node의 첫 번째 = g가 된다.
이 node에서 링크드 리스트의 삭제 방식으로 g를 제거한다.
세그먼트 트리는 아래와 같이 갱신된다. (node의 값은 1 → 0)

같은 방식으로 j, k,e도 모두 삭제했다고 가정하자.

삭제가 되었더라도 세그먼트 트리의 노드에 적힌 index가 갱신되기 때문에,
위와 같은 방법으로 남아있는 알파벳을 잘 찾을 수 있게 된다.
위의 방식은 문자 1개에 대해 구현했기 때문에 세그먼트 트리보다는 링크드 리스트를 이용하는 것이 나을 수 있다.
하지만 문자열이 통째로 들어오는 경우라면 위의 방법도 꽤 효율적이다.
구현은 BOJ 5397 : 키로거 with 세그먼트 트리, 링크드 리스트를 참고하자.
'알고리즘 > [EXP] 삼성 SW 역량 테스트 C형' 카테고리의 다른 글
| 긴자리 후위 표기법 구현하기 (0) | 2023.08.25 |
|---|---|
| BOJ 5397 : 키로거 with 세그먼트 트리, 링크드 리스트 (0) | 2023.08.25 |
| 2차원 배열 탐색과 캐시 미스 (Cache Misses in 2D Arrays) (0) | 2023.08.15 |
| 타입 캐스팅으로 한 번에 메모리 쓰기, 읽기 (Memory Write and Read with Type Casting) (0) | 2023.08.15 |
| 타입 캐스팅으로 deep copy, memcpy 구현하기 (Memory Copy with Type Casting) (0) | 2023.08.15 |




댓글