참고
- 스택
- 볼록 껍질 (Convex Hull, Graham Scan)
- 컨벡스 헐로 임의의 점을 모두 포함하는 사각형 구하기
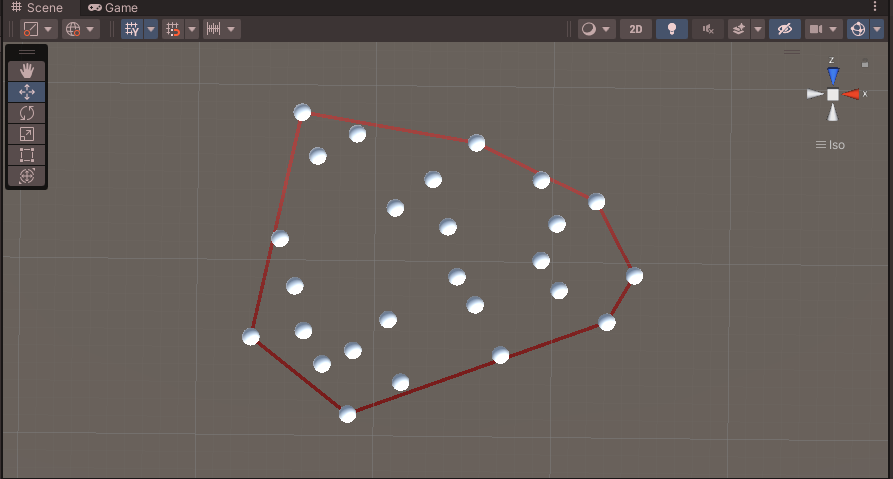
아래와 같이 임의의 점이 불규칙하게 있다고 가정하자.

컨벡스 헐(그레이엄 스캔)을 이용하면 아래와 같이 모든 점을 포함하는 볼록 다각형을 만들 수 있다.
구현
구현은 BOJ 1708 - 볼록 껍질을 참고해서 C# 버전으로 만든다.
유니티에서는 (x, y)가 아니라 (x, z)에서 가장 작은 좌표를 먼저 찾는다.
Vector3 findMinXZ(List<Vector3> position)
{
Vector3 min = new Vector3(100000, 0, 100000);
foreach (Vector3 p in position)
{
if (min.z >= p.z)
{
if (min.z == p.z)
{
if (min.x > p.x)
{
min = p;
}
}
else
{
min = p;
}
}
}
return min;
}
ccw 알고리즘은 Vector가 있으므로 아래와 같이 만들 수 있다.
float ccwBy2D(Vector3 a, Vector3 b, Vector3 c)
{
Vector3 p = b - a;
Vector3 q = c - b;
return Vector3.Cross(p, q).y;
}
리스트(List) 정렬을 위한 compare 함수는 다음과 같다.
int compare(Vector3 a, Vector3 b)
{
float tmp = ccwBy2D(minXZ, a, b);
if (tmp > 0) return -1;
else if (tmp == 0 && (Vector3.Distance(minXZ, a) < Vector3.Distance(minXZ, b))) return -1;
return 1;
}
Convex Hull 알고리즘을 C# 으로 적용하면 아래와 같다.
디버깅을 위해 allCheck와 depth를 추가하여서 depth보다 낮은 단계에서 멈추도록 하였다.
(List<Vector3> convexHull, bool allCheck) getConvexHullVertices(List<Vector3> position, int depth = int.MaxValue)
{
List<Vector3> convexHull = new List<Vector3>();
bool allCheck = true;
int index, sp;
Vector3[] stack = new Vector3[position.Count];
index = sp = 0;
stack[sp++] = position[index++];
stack[sp++] = position[index++];
while (sp < 3)
{
float tmp = ccwBy2D(stack[sp - 2], stack[sp - 1], position[index]);
if (tmp > 0) stack[sp++] = position[index++];
else if (tmp == 0) // 직선인 경우는 점을 교체
{
sp--;
stack[sp++] = position[index++];
}
else index++;
}
while (index < position.Count)
{
if (sp == depth)
{
allCheck = false;
break;
}
float tmp = ccwBy2D(stack[sp - 2], stack[sp - 1], position[index]);
if (tmp > 0) stack[sp++] = position[index++];
else sp--;
}
for (int i = 0; i < sp; i++) convexHull.Add(stack[i]);
return (convexHull, allCheck);
}
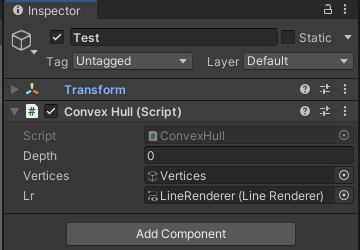
빈 오브젝트에 스크립트를 추가하고 점의 좌표와 라인 렌더러를 설정하자.
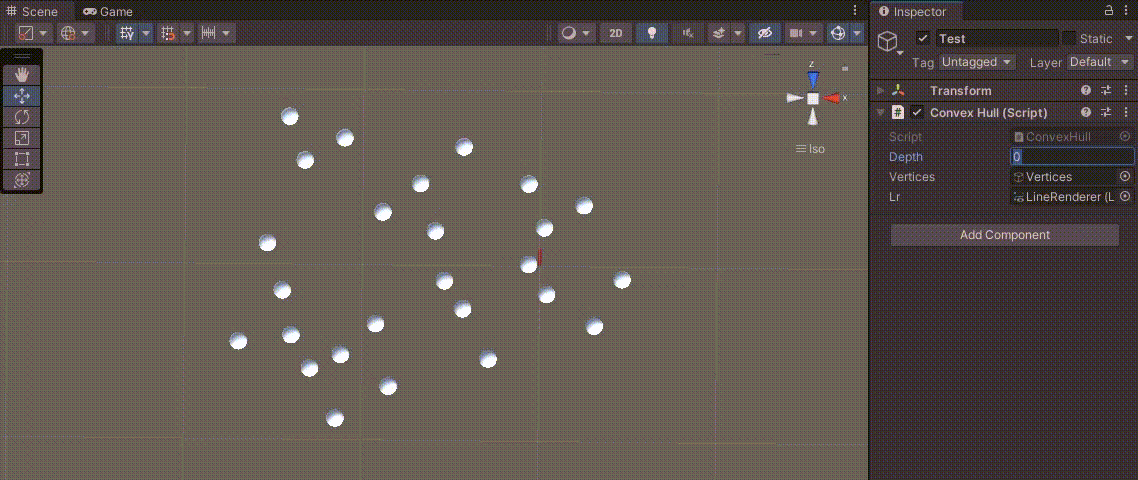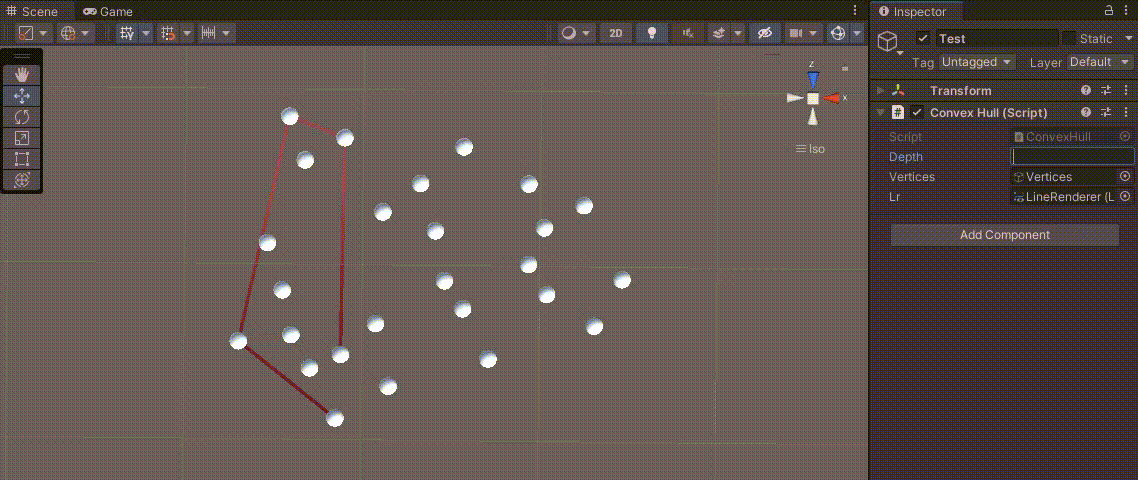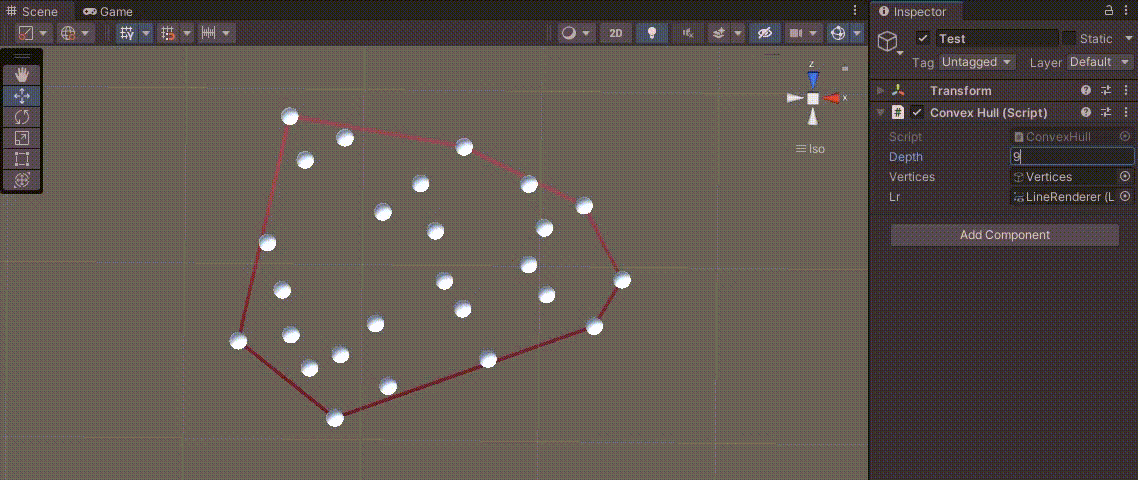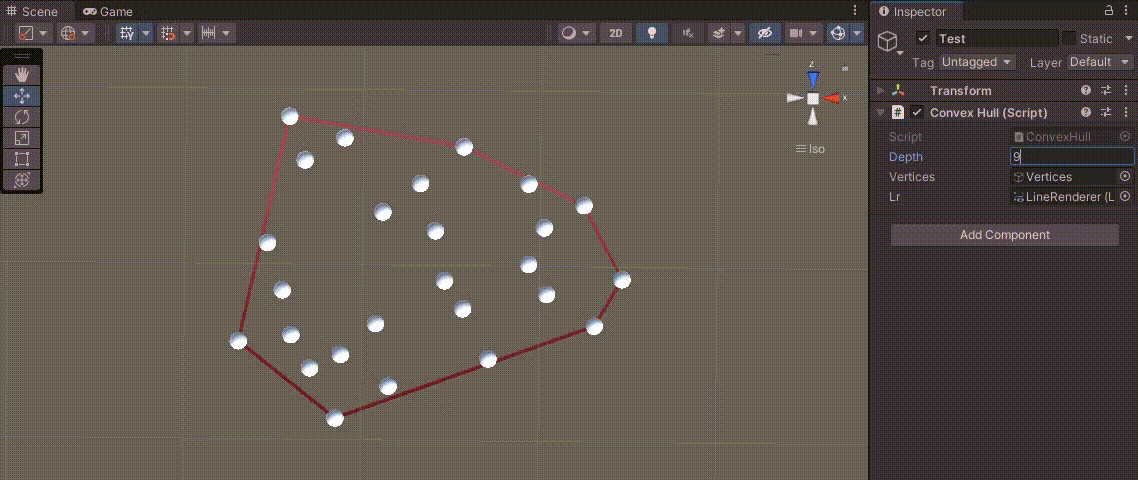
Depth를 조절하면 아래와 같이 점을 모두 포함하는 볼록 다각형을 만들 수 있다.
점의 좌표를 바꿔보아도 볼록 다각형을 잘 만든다.
디버깅이 필요 없다면 getConvexHullVertices는 다음과 같이 수정할 수 있다.
List<Vector3> getConvexHullVertices(List<Vector3> position)
{
List<Vector3> convexHull = new List<Vector3>();
int index, sp;
Vector3[] stack = new Vector3[position.Count];
index = sp = 0;
stack[sp++] = position[index++];
stack[sp++] = position[index++];
while (sp < 3)
{
float tmp = ccwBy2D(stack[sp - 2], stack[sp - 1], position[index]);
if (tmp > 0) stack[sp++] = position[index++];
else if (tmp == 0) // 직선인 경우는 점을 교체
{
sp--;
stack[sp++] = position[index++];
}
else index++;
}
while (index < position.Count)
{
float tmp = ccwBy2D(stack[sp - 2], stack[sp - 1], position[index]);
if (tmp > 0) stack[sp++] = position[index++];
else sp--;
}
for (int i = 0; i < sp; i++) convexHull.Add(stack[i]);
return convexHull;
}
전체 코드는 다음과 같다.
using System.Collections;
using System.Collections.Generic;
using UnityEngine;
public class ConvexHull : MonoBehaviour
{
public int depth;
public GameObject vertices;
Vector3 minXZ;
public LineRenderer lr;
Vector3 findMinXZ(List<Vector3> position)
{
Vector3 min = new Vector3(100000, 0, 100000);
foreach (Vector3 p in position)
{
if (min.z >= p.z)
{
if (min.z == p.z)
{
if (min.x > p.x)
{
min = p;
}
}
else
{
min = p;
}
}
}
return min;
}
float ccwBy2D(Vector3 a, Vector3 b, Vector3 c)
{
Vector3 p = b - a;
Vector3 q = c - b;
return Vector3.Cross(p, q).y;
}
int compare(Vector3 a, Vector3 b)
{
float tmp = ccwBy2D(minXZ, a, b);
if (tmp > 0) return -1;
else if (tmp == 0 && (Vector3.Distance(minXZ, a) < Vector3.Distance(minXZ, b))) return -1;
return 1;
}
(List<Vector3> convexHull, bool allCheck) getConvexHullVertices(List<Vector3> position, int depth = int.MaxValue)
{
List<Vector3> convexHull = new List<Vector3>();
bool allCheck = true;
int index, sp;
Vector3[] stack = new Vector3[position.Count];
index = sp = 0;
stack[sp++] = position[index++];
stack[sp++] = position[index++];
while (sp < 3)
{
float tmp = ccwBy2D(stack[sp - 2], stack[sp - 1], position[index]);
if (tmp > 0) stack[sp++] = position[index++];
else if (tmp == 0) // 직선인 경우는 점을 교체
{
sp--;
stack[sp++] = position[index++];
}
else index++;
}
while (index < position.Count)
{
if (sp == depth)
{
allCheck = false;
break;
}
float tmp = ccwBy2D(stack[sp - 2], stack[sp - 1], position[index]);
if (tmp > 0) stack[sp++] = position[index++];
else sp--;
}
for (int i = 0; i < sp; i++) convexHull.Add(stack[i]);
return (convexHull, allCheck);
}
void setLineRenderer(LineRenderer lr, List<Vector3> vertices, bool check)
{
lr.loop = check;
lr.positionCount = vertices.Count;
lr.SetPositions(vertices.ToArray());
}
void Start()
{
lr.startWidth = lr.endWidth = .2f;
lr.material.color = Color.red;
}
void Update()
{
List<Vector3> position = new List<Vector3>();
foreach (Transform tr in vertices.transform) position.Add(tr.position);
minXZ = findMinXZ(position);
position.Sort(compare);
if (depth == 0) return;
(List<Vector3> convexHull, bool allCheck) = getConvexHullVertices(position, depth);
setLineRenderer(lr, convexHull, allCheck);
}
}
위의 실행결과는 아래의 unitypackage에서 확인 가능하다.
Unity Plus:
Easy 2D, 3D, VR, & AR software for cross-platform development of games and mobile apps. - Unity Store
Have a 2D, 3D, VR, or AR project that needs cross-platform functionality? We can help. Take a look at the easy-to-use Unity Plus real-time dev platform!
store.unity.com
Unity Pro:
Unity Pro
The complete solutions for professionals to create and operate.
unity.com
Unity 프리미엄 학습:
Unity Learn
Advance your Unity skills with live sessions and over 750 hours of on-demand learning content designed for creators at every skill level.
unity.com
'개발 > Unity' 카테고리의 다른 글
| 유니티 - 라인 렌더러로 그리드 만들기 (Make Grid with LineRenderer) (0) | 2023.01.01 |
|---|---|
| 유니티 - 컨벡스 헐로 임의의 점을 모두 포함하는 사각형 구하기 (Points in a Rectangle with Convex Hull) (0) | 2022.12.28 |
| 유니티 - 스톱워치로 실행시간 확인하기 (Unity Stopwatch Timer) (1) | 2022.12.16 |
| 유니티 - 임의의 다각형을 포함하는 사각형 구하기 (Polygon in a Rectangle) (1) | 2022.12.10 |
| 유니티 - 3차원에서 점과 직선 사이의 수선의 발 구하기 (Find a Point Perpendicular to a Line) (0) | 2022.12.10 |




댓글