A형 필수 알고리즘을 체계적으로 배우고 싶다면? (인프런 바로가기)
참고
swexpertacademy.com/main/sst/intro.do
SW Expert Academy에서 C형 샘플 문제 블록 부품 맞추기를 풀어보자.
블록 부품 맞추기는 C형 샘플 문제지만 B형 유형으로 풀 수 있다.
여기서 필요한 개념은 2차원 배열의 해싱과 정렬(merge sort), 그리고 이분 탐색이다.
보통 어떤 데이터를 빠르게 찾고 싶은 경우, 정렬을 한 후에 이분 탐색을 하는 경우가 많다.
문제의 예시를 보자.
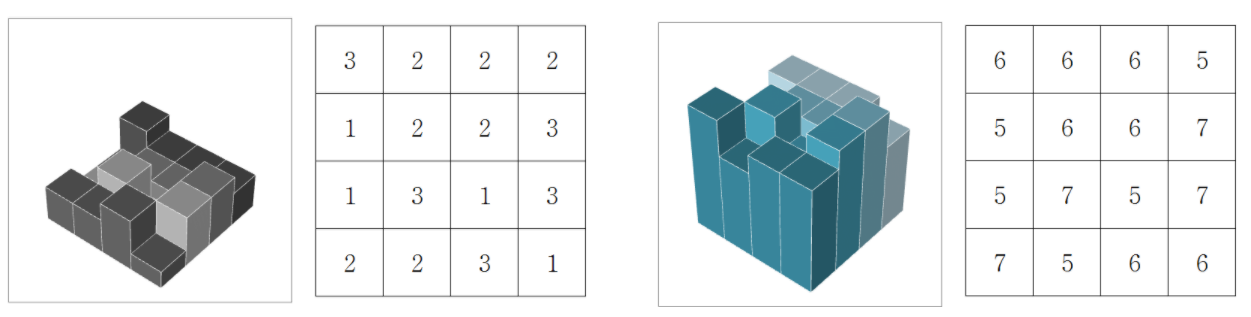
오른쪽의 블럭을 뒤집어서 맞춰 끼우면 모두 높이가 8인 완벽한 육면체가 된다.
총 30,000개의 블럭 중에 완성품의 합이 최대가 되도록 블럭을 맞춰야한다.
먼저 블럭 배열에 번호를 매겨보자.
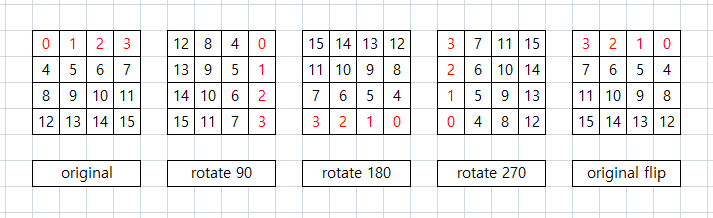
블럭은 1개를 original과 rotate를 3번한 것, 그리고 뒤집은 것 하나로 나눈다.
뒤집은 배열을 기준으로 original과 rotate된 블럭과 맞춰가며 완전한 블럭을 찾으면 된다.
블럭을 쉽게 맞추기 위해 hashing을 하고, 블럭의 번호와 가장 큰 높이와 가장 작은 높이를 저장한다.
original과 rotate된 블럭은 block 배열에 저장하고, flip된 블럭은 match 배열에 저장한다.
높이의 차가 1인 경우는 block1, match1에, 높이의 차가 2인 경우는 block2, match2에 저장한다.
왜냐하면 높이의 차가 1인 block은 절대 높이의 차가 2인 block과 합쳐서 완전해질 수 없기 때문이다.
typedef struct st
{
int index; /* 블럭의 번호 0 ~ 29999 */
int min; /* 가장 작은 높이 */
int max; /* 가장 큰 높이 */
ull hash; /* hashing 된 블럭 */
}BLOCK;
BLOCK block1[30300 * 5];
BLOCK match1[30300];
BLOCK block2[30300 * 5];
BLOCK match2[30300];
int bcnt1, bcnt2, mcnt1, mcnt2;
높이가 0인 경우는 저장하지 않는다.
main함수를 보면 base가 1에서 rand() % 6을 더하므로 1~6의 높이가 되고,
다시 base에 rand() % 3을 더하므로 높이의 차는 0~2가 된다.
int main(void)
{
static int module[MAX][4][4];
srand(3); // 3 will be changed
for (int tc = 1; tc <= 10; tc++)
{
for (int c = 0; c < MAX; c++)
{
int base = 1 + (rand() % 6);
for (int y = 0; y < 4; y++)
{
for (int x = 0; x < 4; x++)
{
module[c][y][x] = base + (rand() % 3);
}
}
}
cout << "#" << tc << " " << makeBlock(module) << endl;
}
return 0;
}따라서 경우를 높이의 차이가 0, 1, 2가 되는 경우로 나눌 수 있다.
하지만 모두 높이가 같은 경우는?
확률을 보면 (1/3)16 = 1 / 43,046,721로 tc 10개 x 블럭 30000개에 대해서 나올 확률이 매우 낮다.
그리고 최소 블럭이 2개가 나와야 한다.
(실제 test를 해본 결과 높이가 모두 같은 두 블럭은 나오지 않았다.)
따라서 모든 블럭의 높이가 같은 경우를 제외하고,
블럭 높이의 차이가 1과 2인 경우로만 나눈다.
이제 블럭을 hasing해보자. 어떻게 hasing하면 블럭을 완전한 블럭으로 쉽고 빠르게 판단할 수 있을까?

여러 방법이 있지만, 오른쪽의 블럭은 0x3222122313132231로 unsigned long long int로 만들면 된다.
그러면 왼쪽의 블럭을 flip하고 hashing하면 0x5666766575756657이 되고 아래와 같이 더하면
0x3222122313132231
0x5666766575756657
= 0x8888888888888888
로 모두 높이가 8인 블럭이 됨을 알 수 있다.
여기서 문제는 완전한 블럭이 0x1111111111111111 ~ 0xFFFFFFFFFFFFFFFF로 총 15개가 된다는 점이다.
(모두 높이가 같은 경우와 같은 논리로 모두 높이가 8인 블럭 2개는 존재하지 않는다고 가정한다.)
따라서 합쳐진 블럭의 최대 높이를 구하기 위해, 블럭을 가장 작은 높이로 모두 깎아버리고,
완전한 블럭은 0x1111111111111111과 0x2222222222222222로만 판단한다.
블럭을 만드는 함수는 아래와 같이 만들어진다.
1) 블럭을 돌면서 블럭의 높이 min과 max를 구한다.
2) max와 min의 차이가 1이면 block1, match1, 차이가 2면 block2, match2에 블럭을 저장한다.
3) original과 rotate는 block 배열에, flip은 match 배열에 저장한다.
4) hashing된 값에서 최소 높이를 뺀다.
#define COMPLETE1 (0x1111111111111111)
#define COMPLETE2 (0x2222222222222222)
void makeHash(int module[][4][4])
{
ull cut[9] = { 0,
0x1111111111111111, 0x2222222222222222, 0x3333333333333333,
0x4444444444444444, 0x5555555555555555, 0x6666666666666666,
0x7777777777777777, 0x8888888888888888 };
register int i, k, min, max, diff;
register ull hash;
for (i = 0; i < 30000; i++)
{
register ui* ptr = (ui*)module[i][0];
min = 10;
max = 0;
for (k = 0; k < 16; k++)
{
max = max < ptr[k] ? ptr[k] : max;
min = min > ptr[k] ? ptr[k] : min;
}
diff = max - min;
register BLOCK* block = (diff == 1) ? block1 : block2;
register BLOCK* match = (diff == 1) ? match1 : match2;
register int& bcnt = (diff == 1) ? bcnt1 : bcnt2;
register int& mcnt = (diff == 1) ? mcnt1 : mcnt2;
hash = (ull)ptr[0] << 60 | (ull)ptr[1] << 56 | (ull)ptr[2] << 52 | (ull)ptr[3] << 48
| (ull)ptr[4] << 44 | (ull)ptr[5] << 40 | (ull)ptr[6] << 36 | (ull)ptr[7] << 32
| (ull)ptr[8] << 28 | (ull)ptr[9] << 24 | (ull)ptr[10] << 20 | (ull)ptr[11] << 16
| (ull)ptr[12] << 12 | (ull)ptr[13] << 8 | (ull)ptr[14] << 4 | (ull)ptr[15];
hash -= cut[min];
block[bcnt].hash = hash;
block[bcnt].min = min;
block[bcnt].max = max;
block[bcnt++].index = i;
hash = (ull)ptr[12] << 60 | (ull)ptr[8] << 56 | (ull)ptr[4] << 52 | (ull)ptr[0] << 48
| (ull)ptr[13] << 44 | (ull)ptr[9] << 40 | (ull)ptr[5] << 36 | (ull)ptr[1] << 32
| (ull)ptr[14] << 28 | (ull)ptr[10] << 24 | (ull)ptr[6] << 20 | (ull)ptr[2] << 16
| (ull)ptr[15] << 12 | (ull)ptr[11] << 8 | (ull)ptr[7] << 4 | (ull)ptr[3];
hash -= cut[min];
block[bcnt].hash = hash;
block[bcnt].min = min;
block[bcnt].max = max;
block[bcnt++].index = i;
hash = (ull)ptr[15] << 60 | (ull)ptr[14] << 56 | (ull)ptr[13] << 52 | (ull)ptr[12] << 48
| (ull)ptr[11] << 44 | (ull)ptr[10] << 40 | (ull)ptr[9] << 36 | (ull)ptr[8] << 32
| (ull)ptr[7] << 28 | (ull)ptr[6] << 24 | (ull)ptr[5] << 20 | (ull)ptr[4] << 16
| (ull)ptr[3] << 12 | (ull)ptr[2] << 8 | (ull)ptr[1] << 4 | (ull)ptr[0];
hash -= cut[min];
block[bcnt].hash = hash;
block[bcnt].min = min;
block[bcnt].max = max;
block[bcnt++].index = i;
hash = (ull)ptr[3] << 60 | (ull)ptr[7] << 56 | (ull)ptr[11] << 52 | (ull)ptr[15] << 48
| (ull)ptr[2] << 44 | (ull)ptr[6] << 40 | (ull)ptr[10] << 36 | (ull)ptr[14] << 32
| (ull)ptr[1] << 28 | (ull)ptr[5] << 24 | (ull)ptr[9] << 20 | (ull)ptr[13] << 16
| (ull)ptr[0] << 12 | (ull)ptr[4] << 8 | (ull)ptr[8] << 4 | (ull)ptr[12];
hash -= cut[min];
block[bcnt].hash = hash;
block[bcnt].min = min;
block[bcnt].max = max;
block[bcnt++].index = i;
/* flip */
hash = (ull)ptr[3] << 60 | (ull)ptr[2] << 56 | (ull)ptr[1] << 52 | (ull)ptr[0] << 48
| (ull)ptr[7] << 44 | (ull)ptr[6] << 40 | (ull)ptr[5] << 36 | (ull)ptr[4] << 32
| (ull)ptr[11] << 28 | (ull)ptr[10] << 24 | (ull)ptr[9] << 20 | (ull)ptr[8] << 16
| (ull)ptr[15] << 12 | (ull)ptr[14] << 8 | (ull)ptr[13] << 4 | (ull)ptr[12];
hash -= cut[min];
match[mcnt].hash = hash;
match[mcnt].min = min;
match[mcnt].max = max;
match[mcnt++].index = i;
}
}
위의 예시 0x3222122313132231와 0x5666766575756657는 각각 최소 높이가 1, 5이므로,
cut배열에 저장된 값으로 최소 높이를 빼면,
0x2111011202021120 + 0x0111211020201102 = 0x2222222222222222 (COMPLETE2)가 된다.
코드를 좀 더 자세히 설명하면 아래와 같다.
ui* ptr을 module[i][0]으로 받으면 module 배열을 2차원 배열이 아닌 1차원 16개로 접근할 수 있다.
2차원 배열이라도 실제 메모리는 순서대로 정렬되어있기 때문이다.
보통 비트 연산에서는 unsigned로 하는 것이 좋으므로, unsigned int로 ptr을 잡았다.
이 문제에서는 비트 연산 ">>" 을 쓰지 않기 때문에 int로 잡아도 pass한다.
register ui* ptr = (ui*)module[i][0];
hashing은 연산 비용을 줄이기 위해 한번에 만들었다.
이때 ptr은 unsinged int이고,
hash는 unsigned long long int이기 때문에 한번 더 type casting을 해야 비트 손실이 없다.
hash = (ull)ptr[0] << 60 | (ull)ptr[1] << 56 | (ull)ptr[2] << 52 | (ull)ptr[3] << 48
| (ull)ptr[4] << 44 | (ull)ptr[5] << 40 | (ull)ptr[6] << 36 | (ull)ptr[7] << 32
| (ull)ptr[8] << 28 | (ull)ptr[9] << 24 | (ull)ptr[10] << 20 | (ull)ptr[11] << 16
| (ull)ptr[12] << 12 | (ull)ptr[13] << 8 | (ull)ptr[14] << 4 | (ull)ptr[15];
ptr 뒤의 번호는 아래의 그림대로 넣어주면 실제 배열을 변경하지 않고 original, rotate, flip hasing이 완성된다.

이제 makeBlock을 보자.
처음에는 init이 필요하다. block과 match의 index를 초기화한다.
그리고 맞춘 블럭을 찾으면, 사용된 블럭인지 check해야하므로 check 배열 2개를 만든다. (높이의 차가 1, 2)
그리고 match와 block을 merge sort를 이용해 정렬한다.
int check1[30300];
int check2[30300];
...
int makeBlock(int module[][4][4])
{
register int i, sum;
/* init */
bcnt1 = bcnt2 = mcnt1 = mcnt2 = 0;
for (i = 0; i < 30000; i++) check1[i] = check2[i] = 0;
/* hashing */
makeHash(module);
/* 정렬 */
sort(match1, 0, mcnt1 - 1, isMinForMatch);
sort(block1, 0, bcnt1 - 1, isMinForBlock);
sort(match2, 0, mcnt2 - 1, isMinForMatch);
sort(block2, 0, bcnt2 - 1, isMinForBlock);
...
}
맞춘 블럭의 높이가 최대합이 되어야 하므로, 기준이 되는 match는 아래의 비교 함수로 정렬한다.
즉, 높이가 높은 match부터 먼저 찾기 위해 높이를 기준으로 내림차순이 되도록 한다.
int isMinForMatch(BLOCK a, BLOCK b)
{
return (a.max > b.max);
}
block에서 찾아야할 값은 높이가 아니라 hash이므로, hash를 기준으로 오름차순이 되도록 한다.
int isMinForBlock(BLOCK a, BLOCK b)
{
if (a.hash < b.hash) return 1;
if (a.hash == b.hash)
{
if (a.max < b.max) return 1;
return 0;
}
return 0;
}
merge sort 함수는 아래와 같다.
만약 comp 함수 포인터가 잘 이해가 안된다면, 위의 조건대로 2개의 merge sort를 만들자.
void merge(BLOCK* block, int start, int end, int(*comp)(BLOCK, BLOCK))
{
register int mid, i, j, k;
mid = (start + end) >> 1;
i = start;
j = mid + 1;
k = 0;
while (i <= mid && j <= end)
{
if (comp(block[i], block[j])) b[k++] = block[i++];
else b[k++] = block[j++];
}
while (i <= mid) b[k++] = block[i++];
while (j <= end) b[k++] = block[j++];
for (i = start; i <= end; i++)
block[i] = b[i - start];
}
void sort(BLOCK* block, int start, int end, int(*comp)(BLOCK a, BLOCK b))
{
register int mid;
if (start >= end) return;
mid = (start + end) >> 1;
sort(block, start, mid, comp);
sort(block, mid + 1, end, comp);
merge(block, start, end, comp);
}정렬을 했으니 이제 블럭을 찾는다.
정렬을 했으면 원하는 값을 이분 탐색을 이용해 logN만에 찾을 수 있다.
binarysearch 함수로 hash값을 찾으면 된다.
여기서 찾아야할 hash는 COMPLETE된 hash에서 자신의 hash값을 뺀 값이다.
예시의 0x2111011202021120 + 0x0111211020201102 = 0x2222222222222222 를 보면
0x2111011202021120인 블럭은
0x2222222222222222 - 0x2111011202021120= 0x0111211020201102 을 찾아야 한다.
그러므로 binarysearch에는 COMPLETE - match[i].hash를 넘겨 block에서 맞는 hash를 찾게 된다.
int makeBlock(int module[][4][4])
{
/* init */
/* hashing */
/* 정렬 */
sum = 0;
for (i = 0; i < mcnt1; i++)
{
if (check1[match1[i].index]) continue;
check1[match1[i].index] = 1;
register BLOCK find = binarysearch(block1, check1, COMPLETE1 - match1[i].hash, bcnt1);
if (find.min == -1) continue;
sum += find.max + match1[i].min;
check1[find.index] = 1;
}
for (i = 0; i < mcnt2; i++)
{
if (check2[match2[i].index]) continue;
check2[match2[i].index] = 1;
register BLOCK find = binarysearch(block2, check2, COMPLETE2 - match2[i].hash, bcnt2);
if (find.min == -1) continue;
sum += find.max + match2[i].min;
check2[find.index] = 1;
}
return sum;
}블럭을 찾지 못한 경우에는 -1을 넘겨주도록 만들어 continue한다.
블럭을 찾으면 check[find.index] = 1로 표시해서 다음에 한 번 더 찾지 못하도록 하고,
이미 한 번 찾은 블럭을 표시하기 위해 check[match[i].index] = 1로 표시한다.
그렇지 않으면 자기 자신을 rotate/flip한 경우도 완전한 블럭으로 찾기 때문이다.
높이가 1, 2인 두 경우로 나뉘므로, 총 2번 실행하면 된다.
마지막으로 binarysearch를 보자.
binarysearch는 block과 check배열, 그리고 찾아야할 value(hash), 그리고 block의 index가 필요하다.
BLOCK binarysearch(BLOCK* block, int* check, ull value, int bcnt)
{
register int l, r, m;
register BLOCK ret;
l = 0, r = bcnt - 1;
ret.index = ret.hash = ret.max = ret.min = -1;
while (l <= r)
{
m = (l + r) / 2;
if (block[m].hash == value)
{
if (check[block[m].index] == 0) return block[m];
return ret;
}
else if (block[m].hash < value)
l = m + 1;
else
r = m - 1;
}
return ret;
}
이분 탐색은 가운데 값이 자기가 원하는 값인지 먼저 확인한다.
가운데 값이 더 작은 값이라면 원하는 값은 오른쪽에 있으므로, left를 변경하여 왼쪽은 더 이상 안보도록 한다.
가운데 값이 더 큰 값이라면 원하는 값은 왼쪽이므로, right를 변경하여 오른쪽은 더 이상 안보도록 한다.
이 로직이 성립하려면 data가 정렬되어 있어야 한다. 따라서 merge sort로 정렬을 해두었다.
찾은 값이 이전에 찾은 블럭이 아니라면 block을 return하고
이전에 찾았던 블럭이거나 hash값이 없다면 ret(-1을 저장해둔 구조체)를 return한다.
-1을 return해줘야 블럭을 찾았는지, 못 찾았는지 구별이 가능하다.
전체 코드는 아래를 참고하자.
Main
#include <iostream>
#include <stdlib.h>
#define MAX 30000
using namespace std;
extern int makeBlock(int module[][4][4]);
int main(void)
{
static int module[MAX][4][4];
srand(3); // 3 will be changed
for (int tc = 1; tc <= 10; tc++)
{
for (int c = 0; c < MAX; c++)
{
int base = 1 + (rand() % 6);
for (int y = 0; y < 4; y++)
{
for (int x = 0; x < 4; x++)
{
module[c][y][x] = base + (rand() % 3);
}
}
}
cout << "#" << tc << " " << makeBlock(module) << endl;
}
return 0;
}
User Code
int makeBlock(int module[][4][4])
{
}정답
typedef unsigned long long int ull;
typedef unsigned int ui;
#define COMPLETE1 (0x1111111111111111)
#define COMPLETE2 (0x2222222222222222)
typedef struct st
{
int index;
int min;
int max;
ull hash;
}BLOCK;
BLOCK b[30300 * 5]; /* merge sort용 배열 */
BLOCK block1[30300 * 5];
BLOCK match1[30300];
BLOCK block2[30300 * 5];
BLOCK match2[30300];
int bcnt1, bcnt2, mcnt1, mcnt2;
int check1[30300];
int check2[30300];
void makeHash(int module[][4][4])
{
ull cut[9] = { 0,
0x1111111111111111, 0x2222222222222222, 0x3333333333333333,
0x4444444444444444, 0x5555555555555555, 0x6666666666666666,
0x7777777777777777, 0x8888888888888888 };
register int i, k, min, max, diff;
register ull hash;
for (i = 0; i < 30000; i++)
{
register ui* ptr = (ui*)module[i][0];
min = 10;
max = 0;
for (k = 0; k < 16; k++)
{
max = max < ptr[k] ? ptr[k] : max;
min = min > ptr[k] ? ptr[k] : min;
}
diff = max - min;
register BLOCK* block = (diff == 1) ? block1 : block2;
register BLOCK* match = (diff == 1) ? match1 : match2;
register int& bcnt = (diff == 1) ? bcnt1 : bcnt2;
register int& mcnt = (diff == 1) ? mcnt1 : mcnt2;
hash = (ull)ptr[0] << 60 | (ull)ptr[1] << 56 | (ull)ptr[2] << 52 | (ull)ptr[3] << 48
| (ull)ptr[4] << 44 | (ull)ptr[5] << 40 | (ull)ptr[6] << 36 | (ull)ptr[7] << 32
| (ull)ptr[8] << 28 | (ull)ptr[9] << 24 | (ull)ptr[10] << 20 | (ull)ptr[11] << 16
| (ull)ptr[12] << 12 | (ull)ptr[13] << 8 | (ull)ptr[14] << 4 | (ull)ptr[15];
hash -= cut[min];
block[bcnt].hash = hash;
block[bcnt].min = min;
block[bcnt].max = max;
block[bcnt++].index = i;
hash = (ull)ptr[12] << 60 | (ull)ptr[8] << 56 | (ull)ptr[4] << 52 | (ull)ptr[0] << 48
| (ull)ptr[13] << 44 | (ull)ptr[9] << 40 | (ull)ptr[5] << 36 | (ull)ptr[1] << 32
| (ull)ptr[14] << 28 | (ull)ptr[10] << 24 | (ull)ptr[6] << 20 | (ull)ptr[2] << 16
| (ull)ptr[15] << 12 | (ull)ptr[11] << 8 | (ull)ptr[7] << 4 | (ull)ptr[3];
hash -= cut[min];
block[bcnt].hash = hash;
block[bcnt].min = min;
block[bcnt].max = max;
block[bcnt++].index = i;
hash = (ull)ptr[15] << 60 | (ull)ptr[14] << 56 | (ull)ptr[13] << 52 | (ull)ptr[12] << 48
| (ull)ptr[11] << 44 | (ull)ptr[10] << 40 | (ull)ptr[9] << 36 | (ull)ptr[8] << 32
| (ull)ptr[7] << 28 | (ull)ptr[6] << 24 | (ull)ptr[5] << 20 | (ull)ptr[4] << 16
| (ull)ptr[3] << 12 | (ull)ptr[2] << 8 | (ull)ptr[1] << 4 | (ull)ptr[0];
hash -= cut[min];
block[bcnt].hash = hash;
block[bcnt].min = min;
block[bcnt].max = max;
block[bcnt++].index = i;
hash = (ull)ptr[3] << 60 | (ull)ptr[7] << 56 | (ull)ptr[11] << 52 | (ull)ptr[15] << 48
| (ull)ptr[2] << 44 | (ull)ptr[6] << 40 | (ull)ptr[10] << 36 | (ull)ptr[14] << 32
| (ull)ptr[1] << 28 | (ull)ptr[5] << 24 | (ull)ptr[9] << 20 | (ull)ptr[13] << 16
| (ull)ptr[0] << 12 | (ull)ptr[4] << 8 | (ull)ptr[8] << 4 | (ull)ptr[12];
hash -= cut[min];
block[bcnt].hash = hash;
block[bcnt].min = min;
block[bcnt].max = max;
block[bcnt++].index = i;
/* flip */
hash = (ull)ptr[3] << 60 | (ull)ptr[2] << 56 | (ull)ptr[1] << 52 | (ull)ptr[0] << 48
| (ull)ptr[7] << 44 | (ull)ptr[6] << 40 | (ull)ptr[5] << 36 | (ull)ptr[4] << 32
| (ull)ptr[11] << 28 | (ull)ptr[10] << 24 | (ull)ptr[9] << 20 | (ull)ptr[8] << 16
| (ull)ptr[15] << 12 | (ull)ptr[14] << 8 | (ull)ptr[13] << 4 | (ull)ptr[12];
hash -= cut[min];
match[mcnt].hash = hash;
match[mcnt].min = min;
match[mcnt].max = max;
match[mcnt++].index = i;
}
}
int isMinForMatch(BLOCK a, BLOCK b)
{
return (a.max > b.max);
}
int isMinForBlock(BLOCK a, BLOCK b)
{
if (a.hash < b.hash) return 1;
if (a.hash == b.hash)
{
if (a.max < b.max) return 1;
return 0;
}
return 0;
}
void merge(BLOCK* block, int start, int end, int(*comp)(BLOCK, BLOCK))
{
register int mid, i, j, k;
mid = (start + end) >> 1;
i = start;
j = mid + 1;
k = 0;
while (i <= mid && j <= end)
{
if (comp(block[i], block[j])) b[k++] = block[i++];
else b[k++] = block[j++];
}
while (i <= mid) b[k++] = block[i++];
while (j <= end) b[k++] = block[j++];
for (i = start; i <= end; i++)
block[i] = b[i - start];
}
void sort(BLOCK* block, int start, int end, int(*comp)(BLOCK a, BLOCK b))
{
register int mid;
if (start >= end) return;
mid = (start + end) >> 1;
sort(block, start, mid, comp);
sort(block, mid + 1, end, comp);
merge(block, start, end, comp);
}
BLOCK binarysearch(BLOCK* block, int* check, ull value, int bcnt)
{
register int l, r, m;
register BLOCK ret;
l = 0, r = bcnt - 1;
ret.index = ret.hash = ret.max = ret.min = -1;
while (l <= r)
{
m = (l + r) / 2;
if (block[m].hash == value)
{
if (check[block[m].index] == 0) return block[m];
return ret;
}
else if (block[m].hash < value)
l = m + 1;
else
r = m - 1;
}
return ret;
}
int makeBlock(int module[][4][4])
{
register int i, sum;
bcnt1 = bcnt2 = mcnt1 = mcnt2 = 0;
for (i = 0; i < 30000; i++) check1[i] = check2[i] = 0;
makeHash(module);
sort(match1, 0, mcnt1 - 1, isMinForMatch);
sort(block1, 0, bcnt1 - 1, isMinForBlock);
sort(match2, 0, mcnt2 - 1, isMinForMatch);
sort(block2, 0, bcnt2 - 1, isMinForBlock);
sum = 0;
for (i = 0; i < mcnt1; i++)
{
if (check1[match1[i].index]) continue;
check1[match1[i].index] = 1;
register BLOCK find = binarysearch(block1, check1, COMPLETE1 - match1[i].hash, bcnt1);
if (find.min == -1) continue;
sum += find.max + match1[i].min;
check1[find.index] = 1;
}
for (i = 0; i < mcnt2; i++)
{
if (check2[match2[i].index]) continue;
check2[match2[i].index] = 1;
register BLOCK find = binarysearch(block2, check2, COMPLETE2 - match2[i].hash, bcnt2);
if (find.min == -1) continue;
sum += find.max + match2[i].min;
check2[find.index] = 1;
}
return sum;
}
실행시간 약 618ms로 통과할 수 있다.
이분 탐색을 사용하지 않고 더 최적화 하는 방법은 링크를 참고하자.
'알고리즘 > [PRO] 삼성 SW 역량 테스트 B형' 카테고리의 다른 글
| BOJ 9612 : Maximum Word Frequency (0) | 2021.05.09 |
|---|---|
| 최적화) 삼성 C형 샘플 문제 : 블록 부품 맞추기 (0) | 2021.04.03 |
| BOJ 7662 : 이중 우선순위 큐 (1) | 2021.03.24 |
| BOJ 20920 : 영단어 암기는 괴로워 (우선순위 큐 갱신 + Hash Table) (0) | 2021.03.21 |
| BOJ 18139 : Rush Hour Puzzle (해시, 2차원 배열 탐색) (9) | 2021.03.18 |





댓글