Isolation Forest
- 랜덤 분할로 데이터를 고립시키며, 고립되는 데 걸리는 깊이로 이상치를 판단하는 앙상블 기반 알고리즘
- 이상치가 다른 데이터보다 쉽게 분리될 수 있다는 아이디어
- 단일 Tree의 결과가 불안정(편향 / 분산)하여 Bagging을 응용하여 이상치 여부를 나타내는 점수의 신뢰성을 높임.
- 특이치 탐지보다 이상치 탐지에 적합

원리
- 이상치는 정상 데이터보다 쉽게 고립된다. → 고립되는 데 필요한 분기 수(트리 깊이)가 작다.
- 즉, 데이터 공간을 무작위로 분할하면서 특정 데이터 포인트가 얼마나 빨리 고립되는지 측정
1. 무작위 분할 기반 Tree(Isolation Tree, iTree) 생성
- 데이터의 특정 Feature 하나를 랜덤 선택
- 해당 Feature에서 임의의 값으로 분할
- 계속 분할하면서 Leaf Node에 한 개의 데이터만 남을 때까지 진행
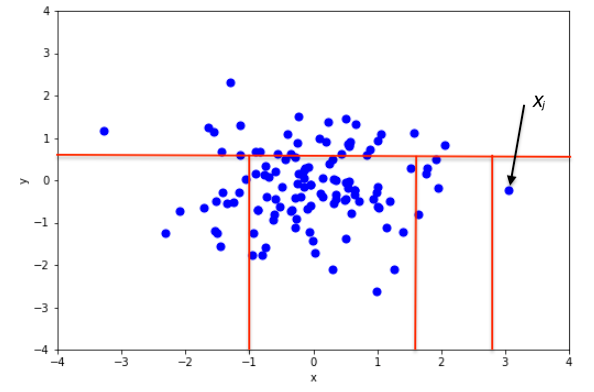
- 이 과정에서 이상치는 다른 점들과 멀리 떨어져 있으므로 몇 번 나누지 않아도 혼자 분리됨
→ 얕은 깊이에서 고립 = 이상치
- 정상치는 많은 점들과 섞여 있어 여러 번 분할되어야 떨어져 나옴
→ 깊은 노드에 위치 = 정상
2. 여러 iTree를 만든다 (앙상블)
- 개별 트리만으로는 랜덤성 때문에 불안정
- n_estimators 개 트리를 만들고 평균 깊이를 사용
3. 고립 난이도 평균값으로 Score 계산
- 평균 깊이 E(h(x)) 를 이용해 이상치 점수(Anomaly Score)를 계산
- 점수가 1에 가까울수록 → 이상치
- 점수가 0에 가까울수록 → 정상
시간 복잡도
- O(T * M * N * logN), T = 트리의 개수
공간 복잡도
- 최대 깊이가 ψ인 이진트리의 공간복잡도 = O(ψ)
장점
- 데이터의 분포나 밀도에 대한 가정을 하지 않음 (다양한 데이터 유형 적용, 비지도 학습)
- 거리 기반 알고리즘(LOF, k-NN)보다 고차원 데이터에서 성능 저하가 상대적으로 적고 효율적인 알고리즘
- 빠른 속도 시간 복잡도 O(n log n), 데이터가 커도 스케일링 잘 됨
- 앙상블 기반으로 안정성 확보, 랜덤 트리 여러 개로 결과 신뢰성 향상
- 이상치 점수 제공 이진 판단뿐 아니라 "이상치 정도" 평가 가능
단점
- 군집형(Local) 이상치 탐지에 약함 → 군집 내부의 미묘한 이상치 탐지가 어려움
ㄴ 데이터 간 관계가 복잡하거나, 이상치가 정상치와 유사한 영역에 분포하면 감지가 어려움
- 랜덤성에 의한 결과 편차 트리 개수가 적으면 불안정
- 스케일 민감성 : Feature 스케일 차이가 크면 분할 과정에서 영향
- 카테고리 데이터 처리 약함, 수치형 기준으로 설계됨 → 전처리 필요
- 이상치 점수는 상대적이므로 임계값 설정이 필요
- 복잡한 비선형 경계 탐지 한계, SVM 등보다 경계가 단순하게 형성됨
- 초기 파라미터 설정 영향 큼 → max_samples, contamination 설정에 민감

하이퍼 파라미터
from sklearn.ensemble import IsolationForest
IsolationForest(
n_estimators=100,
max_samples='auto',
contamination='legacy',
max_features=1.0,
bootstrap=False,
n_jobs=None,
behaviour='old',
random_state=None,
verbose=0,
warm_start=False,
)n_estimators
- 기본 추정기(base estimator) 개수
max_samples
- 각 기본 추정기를 학습시키기 위해 X에서 추출할 샘플 개수
- int : max_samples만큼 샘플 추출
- float : max_samples * X.shape[0]만큼 샘플 추출
- auto : max_samples=min(256, n_samples)로 설정
- max_samples가 전체 샘플 수보다 크면, 모든 트리에 대해 모든 샘플을 사용
contamination
- 데이터셋의 오염 정도, 즉 이상치 비율
- 모델 학습 시 decision function의 임계값(threshold)을 정의할 때 사용
- "auto"로 설정하면, 결정 함수 임계값은 자동 결정
max_features
- 각 기본 추정기를 학습시키기 위해 선택할 feature 수
- int이면 max_features 개 feature 선택
- float이면 max_features * X.shape[1] 개 feature 선택
bootstrap
- True : 개별 트리를 학습할 때 샘플을 복원 추출(with replacement)
- False : 비복원 추출(without replacement)
warm_start
- True : 이전 fit 결과를 재사용하여 estimators를 추가
- False : 새로운 랜덤 포레스트 전체를 학습
Attributes
estimators_ : list of DecisionTreeClassifier
The collection of fitted sub-estimators.
estimators_samples_ : list of arrays
The subset of drawn samples (i.e., the in-bag samples) for each base
estimator.
max_samples_ : integer
The actual number of samples
offset_ : float
Offset used to define the decision function from the raw scores.
We have the relation: ``decision_function = score_samples - offset_``.
Assuming behaviour == 'new', ``offset_`` is defined as follows.
When the contamination parameter is set to "auto", the offset is equal
to -0.5 as the scores of inliers are close to 0 and the scores of
outliers are close to -1. When a contamination parameter different
than "auto" is provided, the offset is defined in such a way we obtain
the expected number of outliers (samples with decision function < 0)
in training.
Assuming the behaviour parameter is set to 'old', we always have
``offset_ = -0.5``, making the decision function independent from the
contamination parameter.
estimators_
- 학습된 하위 추정기(sub-estimator)들의 리스트
estimators_samples_
- 각 기본 추정기에 대해 선택된 샘플(인-백(in-bag) 샘플)의 리스트입니다.
max_samples_
- 실제 사용된 샘플 수
offset_
- raw score로부터 decision_function을 정의할 때 사용되는 오프셋
- decision_function = score_samples - offset_
- behaviour='new'인 경우:
* contamination="auto"이면, offset=-0.5로 설정 (inlier 점수 ~0, outlier 점수 ~-1)
* contamination이 다른 값이면, offset을 조정하여 학습 시 예상되는 이상치 수를 맞춤
- behaviour='old'인 경우:
* 항상 offset=-0.5로 설정되어 contamination과 무관하게 동작
'개발 > Python' 카테고리의 다른 글
| 표본조사와 표본 추출 방법 (0) | 2025.11.23 |
|---|---|
| AgglomerativeClustering (0) | 2025.11.22 |
| LocalOutlierFactor Hyper Parameters and Attributes (0) | 2025.11.22 |
| LightGBM Hyper Parameters and Attributes (0) | 2025.11.22 |
| AdaBoost Hyper Parameters and Attributes (0) | 2025.11.22 |



댓글