어떤 수 하나를 소수 판단할 경우는 링크에서 for문을 돌면서 판단할 수 있다.
하지만 매번 숫자를 소수 판단하면 비용이 많이 들기 때문에,
memoization 기법으로, 특정 숫자가 소수인지 미리 체크해두면 편하다.
이때, 사용하는 알고리즘이 에라토스테네스의 체 이다.
배열 prime[]은 소수인 경우 0, 소수가 아닌 경우 1로 표시하자.
이제 1 ~ 50의 경우 소수를 판단하는 원리를 알아보자.

먼저, 1은 소수가 아니므로 지운다.
prime[1] = 1

이제부터 에라토스테네스의 체가 시작된다.
에라토스테네스의 체에 걸려있지 않다면, 소수다.
현재 2는 에라토스테네스의 체에 걸려있지 않으므로, 소수이다.
그리고 2 부터 2칸씩 모두 소수가 아니므로 지운다.
prime[2 * n] = 1 ( n >= 2 )

지워지는 숫자는 4, 6, 8, ... 으로 2를 제외한 짝수이다.
다음 숫자는 3이고, 3은 에라토스테네스의 체에 걸려있지 않으므로 소수다.
3부터 3칸씩 지워나가면 되지만, 이때 실제로는 3 * 3부터 지워나가면 된다.
이전의 소수에 의해 (2 * 3 < 3 * 3) 이 이미 체에 걸려있기 때문이다.
prime[3 * n] = 1 ( n >= 3 )

다음 숫자 4는 체에 걸려서 넘어가게 된다. 체에 걸려있지 않은 5는 소수다.
prime[5 * n] = 1 ( n >= 5 )

6은 체에 걸렸다. 그리고 7은 체에 걸려있지 않으므로 소수다.
prime[7 * n] = 1 ( n >= 7 )

그 다음 체에 걸려있지 않은 소수는 11이다.
현재 50까지 소수인지 판단하고 있고, 11 * 11은 50보다 크기 때문에 지워나갈 필요가 없다.
따라서 남은 체에 걸려있지 않은 prime[number] = 0인 모든 number는 소수가 된다.

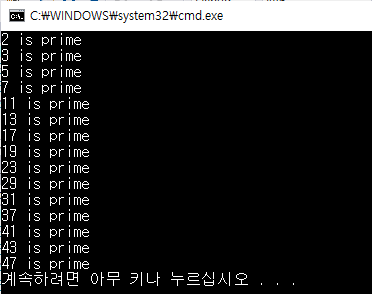
구현 코드와 결과는 아래와 같다.
prime[1]은 예외로 1로 따로 처리한다.
그리고 숫자의 제곱이 검사해야할 숫자들 보다 크면 종료하면 된다. (11을 지울 때 경우를 다시 참고)
지우는 숫자도 선택된 소수의 제곱부터 시작하면 된다. 그 이전의 소수에 의해 모두 지워졌기 때문이다.
#include <stdio.h>
int prime[51];
int main(void)
{
prime[1] = 1;
for (int i = 2; i * i <= 50; i++)
{
if (!prime[i])
{
for (int k = i * i; k <= 50; k += i)
prime[k] = 1;
}
}
for (int num = 1; num <= 50; num++)
if (!prime[num]) printf("%d is prime\n", num);
return 0;
}
prime이 1인 경우 소수라고 정의하면,
가장 처음에 모두 1로 초기화해야하는 코드가 필요하기 때문에 조금 번거롭다.
따라서 prime이 0인 경우에 소수로 정의하도록 하자.
에라토스테네스의 체 관련 문제는 BOJ 6855 골드바흐의 추측을 풀어보자.
'개발 > C, C++' 카테고리의 다른 글
| 제곱근 Square root : 바빌로니아 법 (The Babylonian Method) (0) | 2021.04.09 |
|---|---|
| C++ ofstream을 이용한 FILE 출력 (0) | 2021.03.18 |
| scanf로 문자열과 공백 받기 (0) | 2021.03.16 |
| 소수 판단 함수 (0) | 2021.03.14 |
| C, C++ - 정수로된 FILE 입력 (1) | 2021.03.14 |




댓글