반응형
https://www.acmicpc.net/problem/1395
참고
- 구간 합 구하기 with 탑 다운 세그먼트 트리 (Top-Down Segment Tree)
- 구간 합 구하기 2 with 나중에 업데이트하기 (Top-Down Segment Tree with Lazy Propagation)
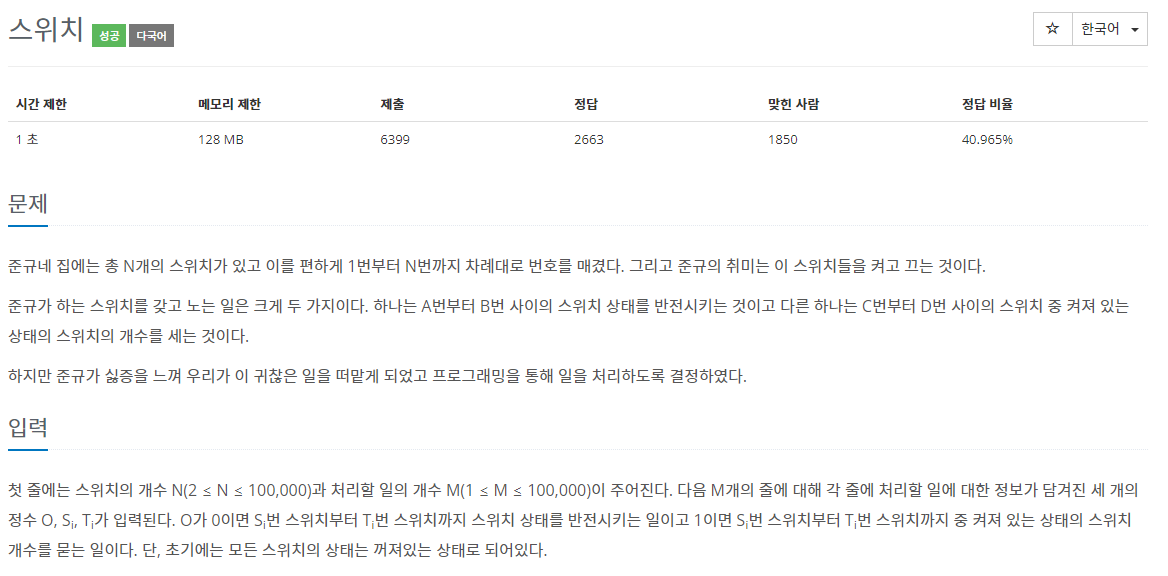
Si ~ Ti까지 스위치를 반전시켜야 하므로, 구간의 갱신이 매우 많다.
따라서 느리게 갱신되는 세그먼트 트리를 이용해서 문제를 풀 수 있다.
예를 들어서 1 ~ 16까지 스위치가 있고 1, 2, 4, 5번 스위치가 켜져있다고 하자.
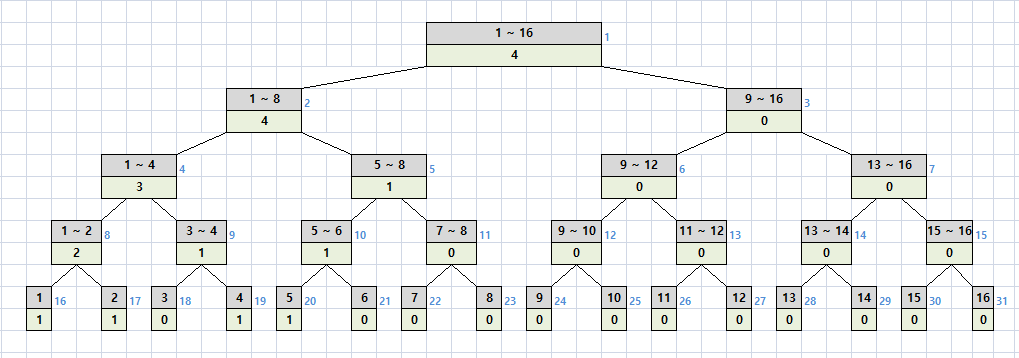
이 상태에서 1 ~ 4번 스위치를 반전시키면 아래와 같이 트리가 갱신되어야 한다.
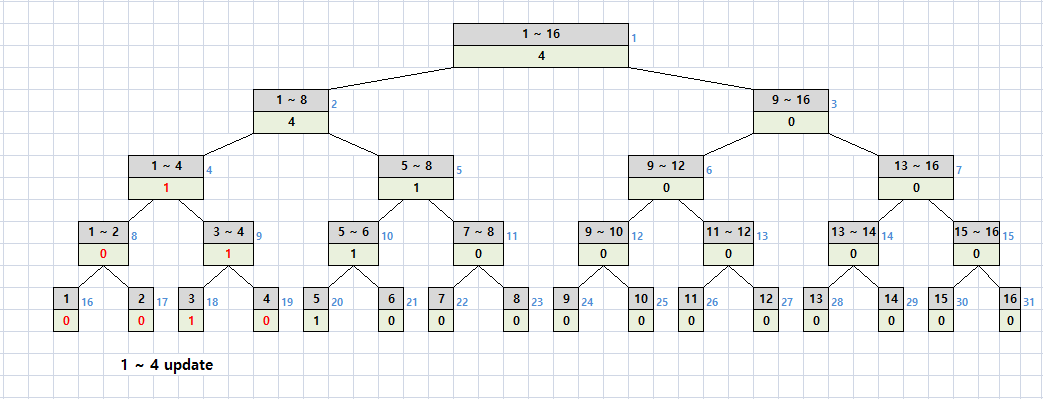
1 ~ 4번의 스위치가 3개 켜져 있는 상태에서 4개의 스위치를 반전시킨다는 것은
전체 스위치의 개수 (4 - 1 + 1)개의 스위치에서 3을 뺀 것과 같은 결과다.
따라서 lazy를 이용하면 아래와 같이 표시할 수 있다.
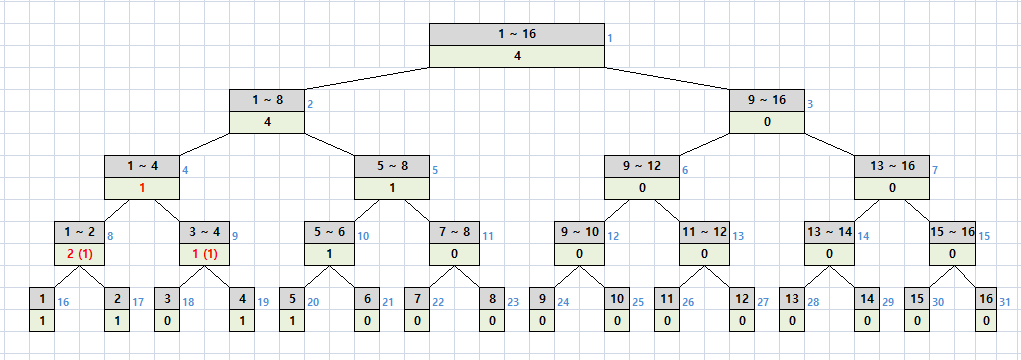
1 ~ 4번 트리는 4개의 구간에서 원래의 값 3을 빼고, 아래의 2개의 노드에 갱신이 필요하다고 lazy를 체크해주면 된다.
그리고 이 lazy는 1일 때만 update를 한다.
lazy가 짝수라면 껐다 켜는 것이므로 원래대로 돌아갈 뿐이다.
따라서 lazy_update는 아래와 같이 구현된다.
void lazy_update(int left, int right, int node)
{
if (lazy[node] == 0) return;
if (lazy[node] & 1) tree[node] = (right - left + 1) - tree[node];
if (left != right)
{
lazy[node * 2] += lazy[node];
lazy[node * 2 + 1] += lazy[node];
}
lazy[node] = 0;
}
전체 코드는 다음과 같다.
#include <stdio.h>
int N, M;
int A[100100];
int tree[400400];
int lazy[400400];
void lazy_update(int left, int right, int node)
{
if (lazy[node] == 0) return;
if (lazy[node] & 1) tree[node] = (right - left + 1) - tree[node];
if (left != right)
{
lazy[node * 2] += lazy[node];
lazy[node * 2 + 1] += lazy[node];
}
lazy[node] = 0;
}
void update(int left, int right, int node, int a, int b, int sw)
{
lazy_update(left, right, node);
if (b < left || right < a) return;
if (a <= left && right <= b)
{
tree[node] = (right - left + 1) - tree[node];
if (left != right)
{
lazy[node * 2] += sw;
lazy[node * 2 + 1] += sw;
}
return;
}
int mid = (left + right) / 2;
update(left, mid, node * 2, a, b, sw);
update(mid + 1, right, node * 2 + 1, a, b, sw);
tree[node] = tree[node * 2] + tree[node * 2 + 1];
}
int getSum(int left, int right, int a, int b, int node)
{
lazy_update(left, right, node);
if (b < left || right < a) return 0;
if (a <= left && right <= b) return tree[node];
int mid = (left + right) / 2;
return getSum(left, mid, a, b, node * 2) + getSum(mid + 1, right, a, b, node * 2 + 1);
}
int main(void)
{
scanf("%d %d", &N, &M);
for (int i = 0; i < M; i++)
{
int o, s, t;
scanf("%d %d %d", &o, &s, &t);
if (o) printf("%d\n", getSum(1, N, s, t, 1));
else update(1, N, 1, s, t, 1);
}
return 0;
}반응형
'알고리즘 > BAEKJOON' 카테고리의 다른 글
| BOJ 6549 : 히스토그램에서 가장 큰 직사각형 (0) | 2023.01.20 |
|---|---|
| BOJ 3653 : 영화 수집 (0) | 2023.01.20 |
| BOJ 14427 : 수열과 쿼리 15 with 세그먼트 트리 (0) | 2023.01.19 |
| BOJ 1572, 9426 : 중앙값 측정 (0) | 2023.01.19 |
| BOJ 1655 : 가운데를 말해요 with 세그먼트 트리 (0) | 2023.01.19 |




댓글