https://www.acmicpc.net/problem/2042
참고
- 구간 합 구하기 with 제곱근 분할법 (Sqrt Decomposition)
- 구간 합 구하기 with 탑 다운 세그먼트 트리 (Top-Down Segment Tree)
- 구간 합 구하기 with 다이나믹 세그먼트 트리 (Dynamic Segment Tree)
- 구간 합 구하기 with 바텀 업 세그먼트 트리 (Bottom-Up Segment Tree)
- 구간 합 구하기 2 with 나중에 업데이트하기 (Top-Down Segment Tree with Lazy Propagation)

여러 배열이 있고 구간의 합이 쿼리로 주어지면 합을 구해서 답을 구하는 문제다.
탑 다운 세그먼트 트리를 이용하여 구간 합을 구해보자.
초기화
주어진 구간의 합을 구해야할 배열이 다음과 같다고 하자.

7개의 원소를 가지기 때문에 트리의 가장 위에는 1 ~ 7번째 원소의 합이 저장되고,
다음 2개의 노드에는 1 ~ 4번째 원소의 합, 5 ~ 7 번째 원소의 합이 저장된다.
그 다음 4개의 노드는 1 ~ 2 / 3 ~ 4 / 5 ~ 6 / 7 번째 원소의 합이 저장된다.
위 과정을 그림으로 그려보자.
가장 위에 있는 노드에서는 1 ~ 7의 합이 저장되어야 한다. (node = 1이 된다.)

그러기 위해서는 먼저 1 ~ 4의 합을 알아야 한다.

그리고 1 ~ 4의 합을 구하기 위해 1 ~ 2의 합을 구해야 한다.

1 ~ 2의 합을 구하기 위해 1과 2의 합을 구한다.

위 과정은 재귀 함수를 이용하여 구현이 가능하다.
구간의 범위 left ~ right가 들어오면 위의 node에 값을 채우기 위해 반으로 나누면서 값을 채운다.
구간 1 ~ 2의 node는 왼쪽 노드(node * 2) 와 오른쪽 노드(node * 2 + 1) 의 합이다.
ll init(int left, int right, int node)
{
if (left == right) return tree[node] = arr[left];
int mid = (left + right) / 2;
return tree[node]
= init(left, mid, node * 2) + init(mid + 1, right, node * 2 + 1);
}
1 ~ 2가 구해졌으므로 다음은 3 ~ 4를 구하게 된다.

init이 완료된 인덱스를 그려보면 아래와 같다.
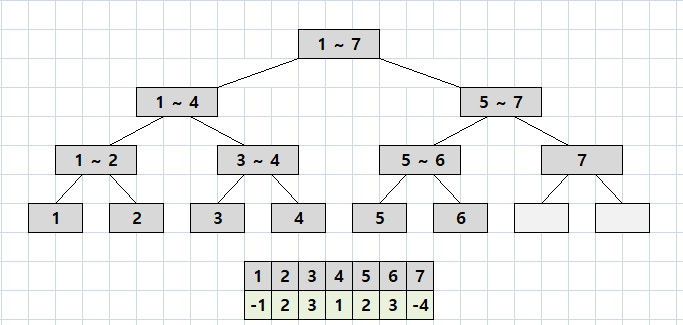
그리고 tree에 들어가 있는 값은 아래와 같다.
각 node는 왼쪽 노드(node * 2) 와 오른쪽 노드(node * 2 + 1)의 합임을 알 수 있다.

구간의 합
1 ~ 7번째 원소의 합을 구한다고 가정해보자.
그러면 첫 번째 노드를 구하면 되므로 tree[1]에 답이 저장되어 있다.
만약 2 ~ 5번째 원소의 합을 구한다고 해보자.
그림으로 그려보면 2 + [3 ~ 4] + 5를 구하면 된다.
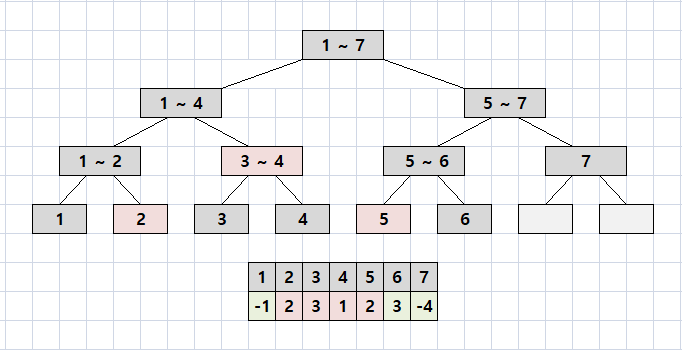
1 ~ 7이 저장되는 segment tree에서 2 ~ 5 구간을 구해야 한다.
1 ~ 7을 반으로 나누면 1 ~ 4 / 5 ~ 7이 되고,
1 ~ 4를 반으로 나누면 1 ~ 2 / 3 ~ 4가 된다.
이때, 3 ~ 4 는 2 ~ 5 구간에 포함되므로 더 이상 내려가지 않는다.
다시 1 ~ 2를 반으로 나누면 1 / 2가 되고, 2는 2 ~ 5 구간에 포함되므로 여기서 종료한다.
다시 5 ~ 7을 반으로 나누면 5 ~ 6 / 7이 되고
5 ~ 6을 반으로 나누면 5 / 6이 된다.
5는 2 ~ 5 구간에 포함되므로 종료한다.
그 외 2 ~ 5 구간을 벗어나는 1이나 6, 7은 0을 return하고, 종료된 시점의 값을 모두 더하면 구간의 합을 구할 수 있다.
ll getSum(int left, int right, int a, int b, int node)
{
if (b < left || right < a) return 0;
if (a <= left && right <= b) return tree[node];
int mid = (left + right) / 2;
return getSum(left, mid, a, b, node * 2) + getSum(mid + 1, right, a, b, node * 2 + 1);
}트리의 갱신
5번째 원소의 2를 -2로 값을 바꿔보자.
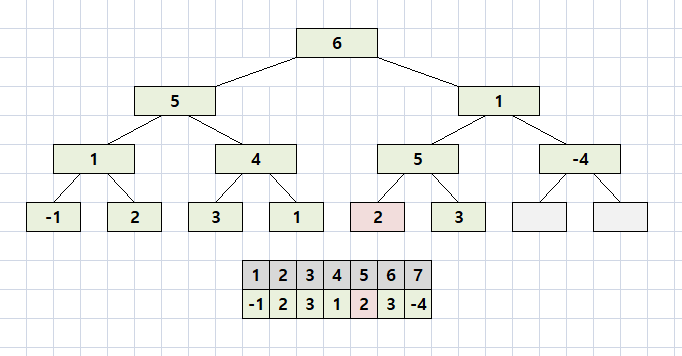
각 node에는 아래 2개의 node의 합이 저장되어 있으므로, 관련된 node를 모두 변경해줘야 한다.
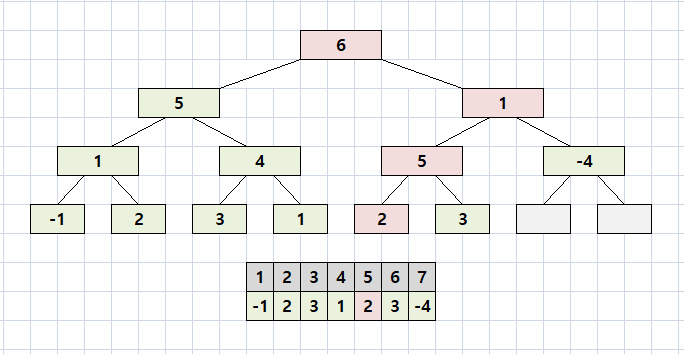
5번째 원소를 -2로 바꿔보자.
하지만 실제로 2 → -2로 바꾸는 것이 아니라 2에서 4를 빼야 한다.
-2로 교체해버리면 다른 node에서 어떤 값으로 바꿔야 할지 알 방법이 없다.
즉, 관련된 모든 구간에 4를 빼는 것이 간편하다.
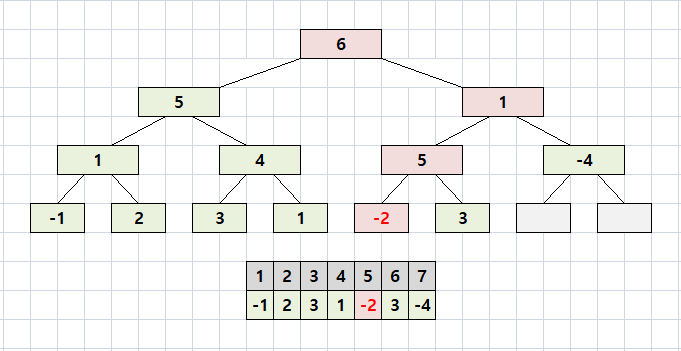
따라서 실제 구현은 1 ~ 7 구간을 반으로 나눠가면서 5가 포함된 구간이 있으면 모두 4를 뺀다.
가장 위의 노드 1 ~ 7 구간은 5를 포함하므로 6에서 4를 뺀 2로 수정된다.
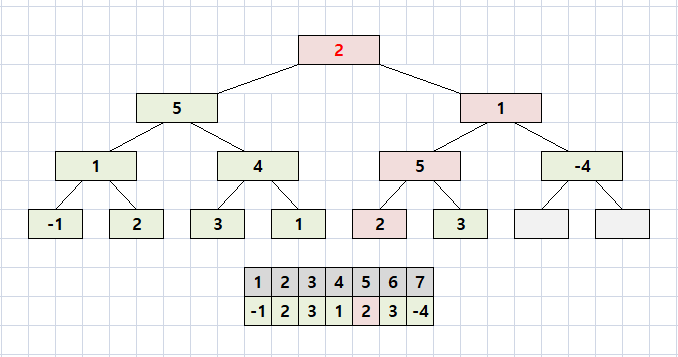
구간 1 ~ 7을 반으로 나누면 1 ~ 4와 5 ~ 7이 된다.
5 ~ 7만 5가 포함되므로 -1에 4를 빼서 -4로 갱신한다.
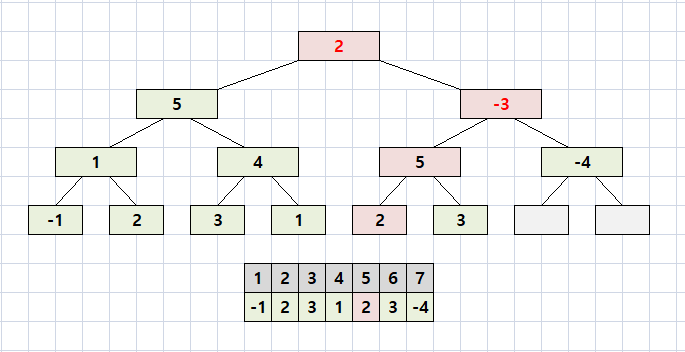
5 ~ 7은 5 ~ 6 / 7로 나뉘고 5 ~ 6만 5가 포함된다.
따라서 5에서 4를 뺀 1로 갱신된다.
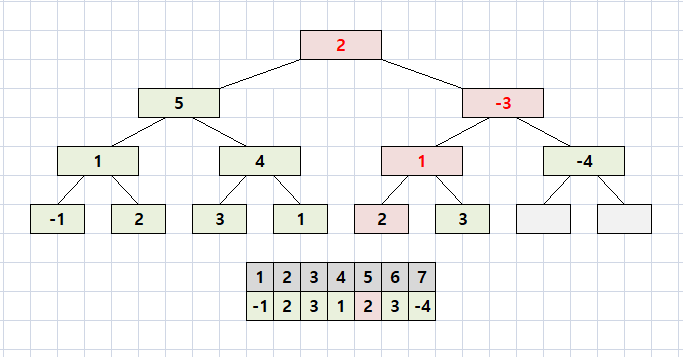
마지막으로 5 ~ 6은 5 / 6으로 나뉘고, 5만 갱신한다.
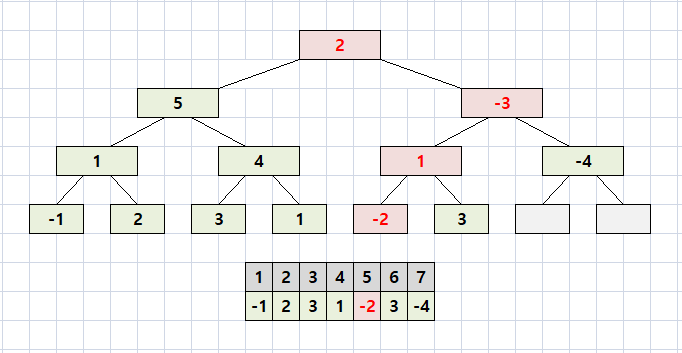
구간을 갱신했더라도 각 node는 왼쪽 노드(node * 2) 와 오른쪽 노드(node * 2 + 1)의 합임을 알 수 있다.
구현
위의 내용을 바탕으로 전체 구현한 내용은 다음과 같다.
tree는 주어진 N에 가장 2의 배수에 근접한 값의 2배로 잡으면 되는데, (1,000,000 → 1,048,576 → 2,097,152)
메모리가 넉넉하다면 4배로 잡으면 충분하다.
#include <stdio.h>
typedef long long int ll;
int N, M, K;
ll arr[1001000];
ll tree[4004000];
ll init(int left, int right, int node)
{
if (left == right) return tree[node] = arr[left];
int mid = (left + right) / 2;
return tree[node]
= init(left, mid, node * 2) + init(mid + 1, right, node * 2 + 1);
}
ll getSum(int left, int right, int a, int b, int node)
{
if (b < left || right < a) return 0;
if (a <= left && right <= b) return tree[node];
int mid = (left + right) / 2;
return getSum(left, mid, a, b, node * 2) + getSum(mid + 1, right, a, b, node * 2 + 1);
}
void update(int left, int right, int node, int index, ll diff)
{
if (index < left || right < index) return;
tree[node] += diff;
if (left != right)
{
int mid = (left + right) / 2;
update(left, mid, node * 2, index, diff);
update(mid + 1, right, node * 2 + 1, index, diff);
}
}
int main()
{
scanf("%d %d %d", &N, &M, &K);
for (int i = 1; i <= N; i++) scanf("%lld", &arr[i]);
init(1, N, 1);
for (int i = 0; i < M + K; i++)
{
int a;
scanf("%d", &a);
if (a == 1)
{
int b;
ll c;
scanf("%d %lld", &b, &c);
update(1, N, 1, b, c - arr[b]);
arr[b] = c;
}
else
{
int b, c;
scanf("%d %d", &b, &c);
printf("%lld\n", getSum(1, N, b, c, 1));
}
}
return 0;
}diff를 이용하지 않고 value로 바로 update하려면 update를 아래와 같이 수정하면 된다.
위의 방식은 내려가면서 diff만큼 증가했다면,
이 방법은 먼저 내려간 다음에 값을 바꾸고 올라가면서 다시 합을 구한다.
void update(int left, int right, int node, int index, ll value)
{
if (index < left || right < index) return;
if (left == right)
{
tree[node] = value;
return;
}
int mid = (left + right) / 2;
int leftNodeIndex = node * 2;
int rightNodeIndex = node * 2 + 1;
update(left, mid, leftNodeIndex, index, value);
update(mid + 1, right, rightNodeIndex, index, value);
tree[node] = tree[leftNodeIndex] + tree[rightNodeIndex];
}
이 방법은 arr를 저장할 필요가 없으므로 아래와 같이 코드가 바뀐다.
(init 제거, diff 대신 value를 그대로 삽입)
#include <stdio.h>
typedef long long int ll;
int N, M, K;
ll tree[4004000];
void update(int left, int right, int node, int index, ll value)
{
if (index < left || right < index) return;
if (left == right)
{
tree[node] = value;
return;
}
int mid = (left + right) / 2;
int leftNodeIndex = node * 2;
int rightNodeIndex = node * 2 + 1;
update(left, mid, leftNodeIndex, index, value);
update(mid + 1, right, rightNodeIndex, index, value);
tree[node] = tree[leftNodeIndex] + tree[rightNodeIndex];
}
ll getSum(int left, int right, int a, int b, int node)
{
if (b < left || right < a) return 0;
if (a <= left && right <= b) return tree[node];
int mid = (left + right) / 2;
return getSum(left, mid, a, b, node * 2) + getSum(mid + 1, right, a, b, node * 2 + 1);
}
int main()
{
scanf("%d %d %d", &N, &M, &K);
for (int i = 1; i <= N; i++)
{
ll input;
scanf("%lld", &input);
update(1, N, 1, i, input);
}
for (int i = 0; i < M + K; i++)
{
int a;
scanf("%d", &a);
if (a == 1)
{
int b;
ll c;
scanf("%d %lld", &b, &c);
update(1, N, 1, b, c);
}
else
{
int b, c;
scanf("%d %d", &b, &c);
printf("%lld\n", getSum(1, N, b, c, 1));
}
}
return 0;
}'알고리즘 > [PRO] 삼성 SW 역량 테스트 B형' 카테고리의 다른 글
| BOJ 10999 : 구간 합 구하기 2 with 나중에 업데이트하기 (Top-Down Segment Tree with Lazy Propagation) (0) | 2023.01.16 |
|---|---|
| BOJ 2042 : 구간 합 구하기 with 바텀 업 세그먼트 트리 (Bottom-Up Segment Tree) (0) | 2023.01.15 |
| BOJ 2042 : 구간 합 구하기 with 제곱근 분할법 (Sqrt Decomposition) (0) | 2023.01.15 |
| Indexed Priority Queue - 우선순위 큐의 임의 원소 갱신, 변경 (update) (4) | 2022.01.13 |
| BOJ 14427 : 수열과 쿼리 15 (Reference) (0) | 2021.07.03 |




댓글