참고
2D 복셀을 3D 복셀로 확장해보자.
먼저 voxelData가 2차원 int[,]에서 3차원 int[,,]로 변경된다.
2D에서 [z, x]를 그대로 유지하기 위해 [y, z, x]로 확장한다.
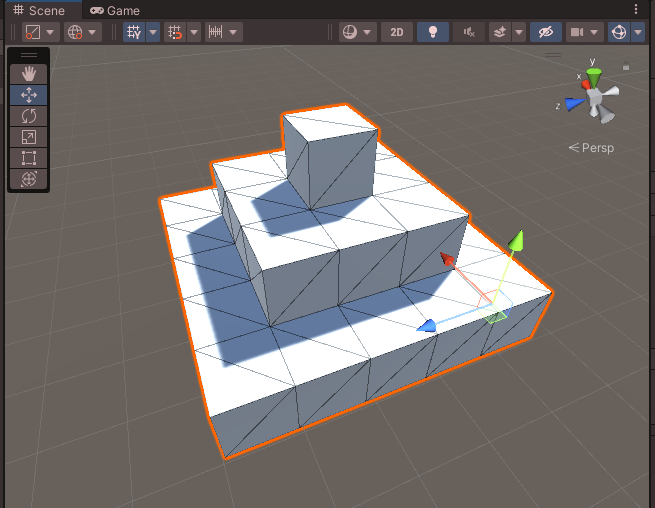
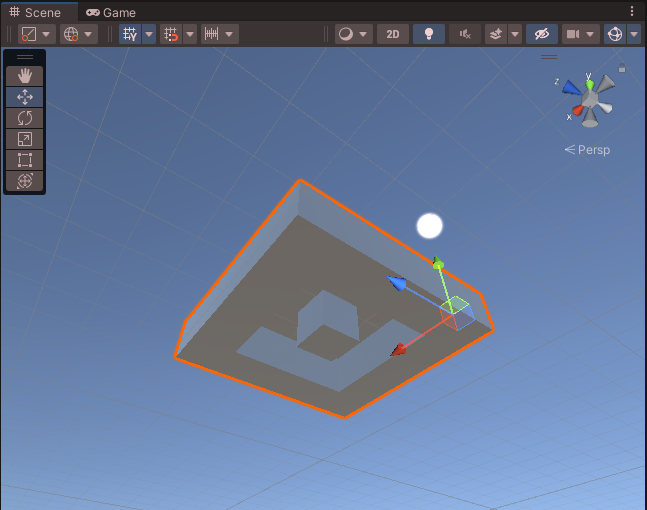
아래의 좌표는 위의 그림에 있는 피라미드가 된다.
int[,,] voxelData = new int[,,] { // [y, z, x]
{ // y = 0
{ 1, 1, 1, 1, 1 }, // => x
{ 1, 0, 0, 0, 1 }, // ↓ z
{ 1, 0, 1, 0, 1 },
{ 1, 0, 0, 0, 1 },
{ 1, 1, 1, 1, 1 },
},
{ // y = 1
{ 0, 0, 0, 0, 0 }, // => x
{ 0, 1, 1, 1, 0 }, // ↓ z
{ 0, 1, 1, 1, 0 },
{ 0, 1, 1, 1, 0 },
{ 0, 0, 0, 0, 0 },
},
{ // y = 2
{ 0, 0, 0, 0, 0 }, // => x
{ 0, 0, 0, 0, 0 }, // ↓ z
{ 0, 0, 1, 0, 0 },
{ 0, 0, 0, 0, 0 },
{ 0, 0, 0, 0, 0 },
},
};
배열의 차원이 바뀌었으므로 yLength를 추가하고 z/xLength도 변경한다.
public int yLength
{
get { return voxelData.GetLength(0); }
}
public int zLength
{
get { return voxelData.GetLength(1); }
}
public int xLength
{
get { return voxelData.GetLength(2); }
}
마찬가지로 y값이 추가된 것에 대해 코드를 확장하였다.
public int getData(int x, int y, int z)
{
return voxelData[y, z, x];
}
public bool isPossibleDrawing(int x, int y, int z, int dir)
{
Vector3Int coord = new Vector3Int(x, y, z) + direction[dir];
if (coord.y < 0 || coord.y >= yLength
|| coord.z < 0 || coord.z >= zLength
|| coord.x < 0 || coord.x >= xLength) return true;
return getData(coord.x, coord.y, coord.z) == 0;
}
면을 그릴 때도 y 좌표를 고려하도록 수정한다.
void makeFace(int x, int y, int z, int dir)
{
for(int i = 0; i < 4; i++)
{
Vector3 v = Vector3.Scale(baseVertices[faceNumber[dir][i]], size) + offset;
v.x += (x * size.x);
v.y += (y * size.y);
v.z += (z * size.z);
vertices.Add(v);
}
int vIdx = vertices.Count;
triangles.Add(vIdx - 4 + 0);
triangles.Add(vIdx - 4 + 1);
triangles.Add(vIdx - 4 + 3);
triangles.Add(vIdx - 4 + 1);
triangles.Add(vIdx - 4 + 2);
triangles.Add(vIdx - 4 + 3);
}
setMeshData가 y에 대해서도 for문을 수행하도록 수정하면 완료된다.
void setMeshData(Voxels voxel)
{
vertices.Clear();
triangles.Clear();
for(int y = 0; y < voxel.yLength; y++)
{
for (int z = 0; z < voxel.zLength; z++)
{
for (int x = 0; x < voxel.xLength; x++)
{
if (voxel.getData(x, y, z) == 0) continue;
for (int dir = 0; dir < 6; dir++)
{
if (voxel.isPossibleDrawing(x, y, z, dir))
{
makeFace(x, y, z, dir);
}
}
}
}
}
}
코드를 실행하면 정상적으로 좌표를 바탕으로 3D Voxel을 만들 수 있다.
전체 코드는 다음과 같다.
using System.Collections;
using System.Collections.Generic;
using UnityEngine;
public class Voxels
{
int[,,] voxelData = new int[,,] { // [y, z, x]
{ // y = 0
{ 1, 1, 1, 1, 1 }, // => x
{ 1, 0, 0, 0, 1 }, // ↓ z
{ 1, 0, 1, 0, 1 },
{ 1, 0, 0, 0, 1 },
{ 1, 1, 1, 1, 1 },
},
{ // y = 1
{ 0, 0, 0, 0, 0 }, // => x
{ 0, 1, 1, 1, 0 }, // ↓ z
{ 0, 1, 1, 1, 0 },
{ 0, 1, 1, 1, 0 },
{ 0, 0, 0, 0, 0 },
},
{ // y = 2
{ 0, 0, 0, 0, 0 }, // => x
{ 0, 0, 0, 0, 0 }, // ↓ z
{ 0, 0, 1, 0, 0 },
{ 0, 0, 0, 0, 0 },
{ 0, 0, 0, 0, 0 },
},
};
Vector3Int[] direction =
{
new Vector3Int(0, 0, +1), // FORWARD
new Vector3Int(+1, 0, 0), // RIGHT
new Vector3Int(0, +1, 0), // UP
new Vector3Int(0, 0, -1), // BACK
new Vector3Int(-1, 0, 0), // LEFT
new Vector3Int(0, -1, 0), // DOWN
};
public int yLength
{
get { return voxelData.GetLength(0); }
}
public int zLength
{
get { return voxelData.GetLength(1); }
}
public int xLength
{
get { return voxelData.GetLength(2); }
}
public int getData(int x, int y, int z)
{
return voxelData[y, z, x];
}
public bool isPossibleDrawing(int x, int y, int z, int dir)
{
Vector3Int coord = new Vector3Int(x, y, z) + direction[dir];
if (coord.y < 0 || coord.y >= yLength
|| coord.z < 0 || coord.z >= zLength
|| coord.x < 0 || coord.x >= xLength) return true;
return getData(coord.x, coord.y, coord.z) == 0;
}
}
[RequireComponent(typeof(MeshRenderer), typeof(MeshFilter))]
public class ProceduralVoxels : MonoBehaviour
{
public Vector3 size = new Vector3(1.0f, 1.0f, 1.0f);
public Vector3 offset = new Vector3(0, 0, 0);
Mesh mesh;
List<Vector3> vertices = new List<Vector3>();
List<int> triangles = new List<int>();
public enum Direction
{
FORWARD, // (0, 0, +1)
RIGHT, // (+1, 0, 0)
UP, // (0, +1, 0)
BACK, // (0, 0, -1)
LEFT, // (-1, 0, 0)
DOWN // (0, -1, 0)
}
public int[][] faceNumber =
{
new int[] {0, 1, 2, 3}, // FORWARD
new int[] {5, 0, 3, 6}, // RIGHT
new int[] {5, 4, 1, 0}, // UP
new int[] {4, 5, 6, 7}, // BACK
new int[] {1, 4, 7, 2}, // LEFT
new int[] {3, 2, 7, 6}, // DOWN
};
Vector3[] baseVertices =
{
new Vector3(+0.5f, +0.5f, +0.5f),
new Vector3(-0.5f, +0.5f, +0.5f),
new Vector3(-0.5f, -0.5f, +0.5f),
new Vector3(+0.5f, -0.5f, +0.5f),
new Vector3(-0.5f, +0.5f, -0.5f),
new Vector3(+0.5f, +0.5f, -0.5f),
new Vector3(+0.5f, -0.5f, -0.5f),
new Vector3(-0.5f, -0.5f, -0.5f),
};
void OnValidate()
{
if (mesh == null) return;
if (size.magnitude > 0 || offset.magnitude > 0)
{
setMeshData(new Voxels());
createProceduralMesh();
}
}
void Start()
{
mesh = GetComponent<MeshFilter>().mesh;
setMeshData(new Voxels());
createProceduralMesh();
}
void makeFace(int x, int y, int z, int dir)
{
for(int i = 0; i < 4; i++)
{
Vector3 v = Vector3.Scale(baseVertices[faceNumber[dir][i]], size) + offset;
v.x += (x * size.x);
v.y += (y * size.y);
v.z += (z * size.z);
vertices.Add(v);
}
int vIdx = vertices.Count;
triangles.Add(vIdx - 4 + 0);
triangles.Add(vIdx - 4 + 1);
triangles.Add(vIdx - 4 + 3);
triangles.Add(vIdx - 4 + 1);
triangles.Add(vIdx - 4 + 2);
triangles.Add(vIdx - 4 + 3);
}
void setMeshData(Voxels voxel)
{
vertices.Clear();
triangles.Clear();
for(int y = 0; y < voxel.yLength; y++)
{
for (int z = 0; z < voxel.zLength; z++)
{
for (int x = 0; x < voxel.xLength; x++)
{
if (voxel.getData(x, y, z) == 0) continue;
for (int dir = 0; dir < 6; dir++)
{
if (voxel.isPossibleDrawing(x, y, z, dir))
{
makeFace(x, y, z, dir);
}
}
}
}
}
}
void createProceduralMesh()
{
mesh.Clear();
mesh.vertices = vertices.ToArray();
mesh.triangles = triangles.ToArray();
mesh.RecalculateNormals();
Destroy(this.GetComponent<MeshCollider>());
this.gameObject.AddComponent<MeshCollider>();
}
}
Unity Plus:
Easy 2D, 3D, VR, & AR software for cross-platform development of games and mobile apps. - Unity Store
Have a 2D, 3D, VR, or AR project that needs cross-platform functionality? We can help. Take a look at the easy-to-use Unity Plus real-time dev platform!
store.unity.com
Unity Pro:
Unity Pro
The complete solutions for professionals to create and operate.
unity.com
Unity 프리미엄 학습:
Unity Learn
Advance your Unity skills with live sessions and over 750 hours of on-demand learning content designed for creators at every skill level.
unity.com




댓글