BOJ 1655 : 가운데를 말해요 with 세그먼트 트리
참고
- 구간 합 구하기 with 탑 다운 세그먼트 트리 (Top-Down Segment Tree)
- 구간 합 구하기 with 바텀 업 세그먼트 트리 (Bottom-Up Segment Tree)
- 구간 합 구하기 with 다이나믹 세그먼트 트리 (Dynamic Segment Tree)
- BOJ 1655 : 가운데를 말해요 with 우선순위 큐
- 세그먼트 트리를 이용한 링크드 리스트의 삽입과 삭제
세그먼트 트리를 이용해 가운데 값을 찾아보자.
세그먼트 트리를 이용하면 index를 잘 관리해서 중앙값을 구할 수 있다.
설명을 위해 입력되는 숫자의 범위가 1 ~ 16이라고 가정하자.
그러면 아래와 같은 트리를 만들어야 한다. (파란색 숫자는 tree의 index)
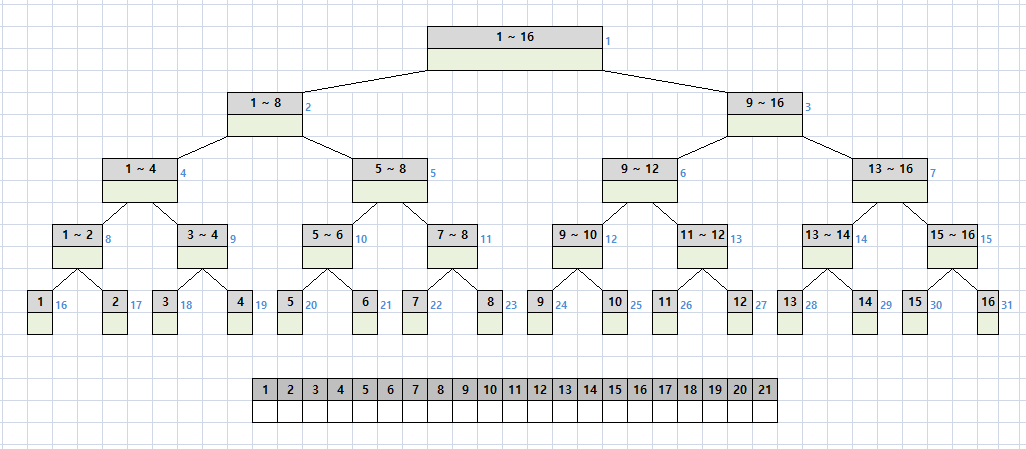
아래의 배열은 숫자를 순서대로 정렬했을 때의 표다.
처음으로 숫자가 4가 입력되었다고 해보자.
이 경우에는 가장 아래의 leaf의 4번째 node = tree의 19번째 node에 1을 증가 시킨다.
그리고 상위 node도 모두 증가시킨다.

그리고 2, 7, 10, 16이 입력되었다고 해보자.
그러며 세그먼트 트리는 아래와 같이 바뀐다.
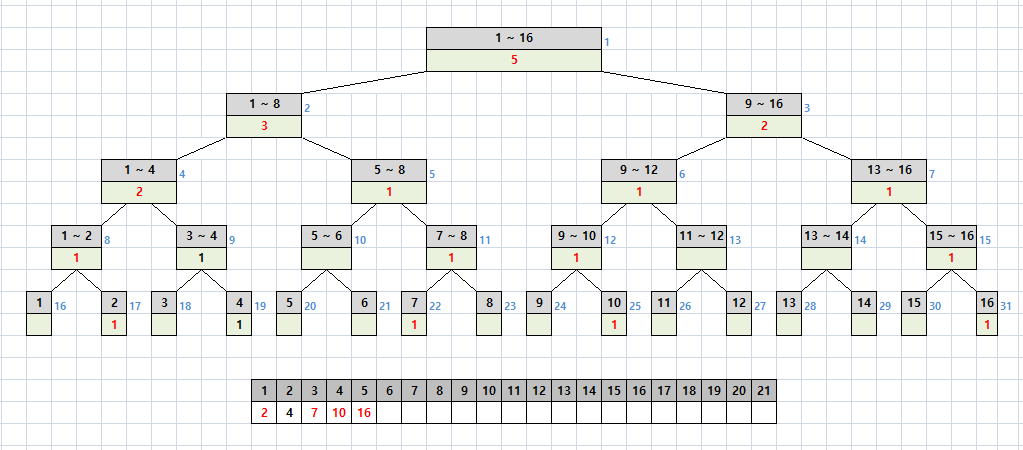
가운데 값 구하기
이제 여기서 가운데 값을 구해보자.
2, 4, 7, 10, 16이 입력되었으므로 답은 7이어야 한다.
현재 입력된 숫자는 총 5개이므로, 3번째 값을 찾아야 한다.
구하는 방법은 다음과 같다.
treeIdx = 1, 찾아야 하는 index = 3이다.
treeIdx의 왼쪽 node에 있는 값과 index를 비교한다.
→ index <= tree[treeIdx * 2] 라면 treeIdx를 2배로 증가한다. (왼쪽 node로 이동)
→ 그렇지 않다면, index에서 tree[treeIdx * 2]를 빼고, treeIdx를 2배 + 1로 증가한다. (오른쪽 node로 이동)
위의 방법을 마지막 leaf의 개수가 될 때까지 반복한다.
현재 그래프의 마지막 leaf의 개수는 16개다. (treeIdx < 16)
실제로 답인 7을 찾는지 확인해보자.
(1) treeIdx = 1, index = 3이고
3 <= tree[treeIdx * 2] = 3을 만족하므로, treeIdx = 2가 된다.
(2) treeIdx = 2, index = 3이고,
3 <= tree[treeIdx * 2] = 2를 만족하지 않으므로, treeIdx = 2 * 2 + 1 = 5가 되고, index -= 2로 1이 된다.
(3) treeIdx = 5, index = 1이고,
1 <= tree[treeIdx * 2] = 0을 만족하지 않으므로, treeIdx = 5 * 5 + 1 = 11이 되고, index -= 0으로 1이 된다.
(4) treeIdx = 11, index = 1이고,
1 <= tree[treeIdx * 2] = 1을 만족하므로, treeIdx = 22가 된다.
마지막 leaf에 도달하였으므로, treeIdx = 22를 구할 수 있다.
이 treeIdx가 22라는 것은 배열이 7이 저장된 곳이다.
마지막 leaf를 제외한 모든 leaf의 개수가 15이기 때문에 treeIdx - 15 = 7을 얻을 수 있게 된다.
그림으로 그려보면 아래와 같다.
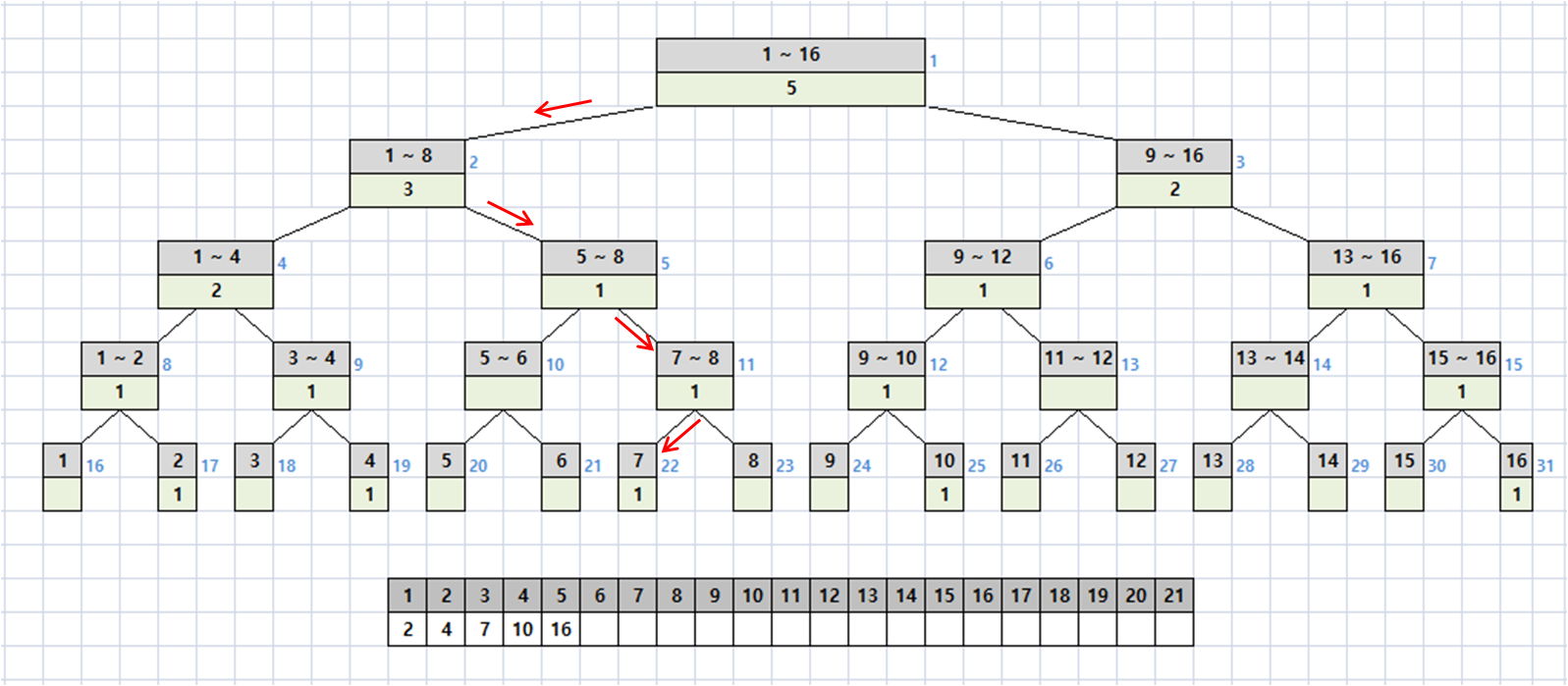
마찬가지로, 이 방법을 이용하면 몇 번째에 어떤 숫자가 있는지 쉽게 알 수 있게 된다.
이 문제에서는 가운데를 구하기 때문에 (i + 1) / 2 번째의 수에 대해서만 답을 찾는다.
중복된 수가 있는 경우 가운데 값을 구하기
숫자가 아래와 같이 더 입력이 되었다고 하자.
중복된 숫자가 포함된 경우에도 위의 방식으로 가운데 숫자를 잘 구하는지 보자.
2, 4, 7, 10, 16에 6이 3개, 7이 1개, 9가 6개가 추가되었다고 가정해보자.
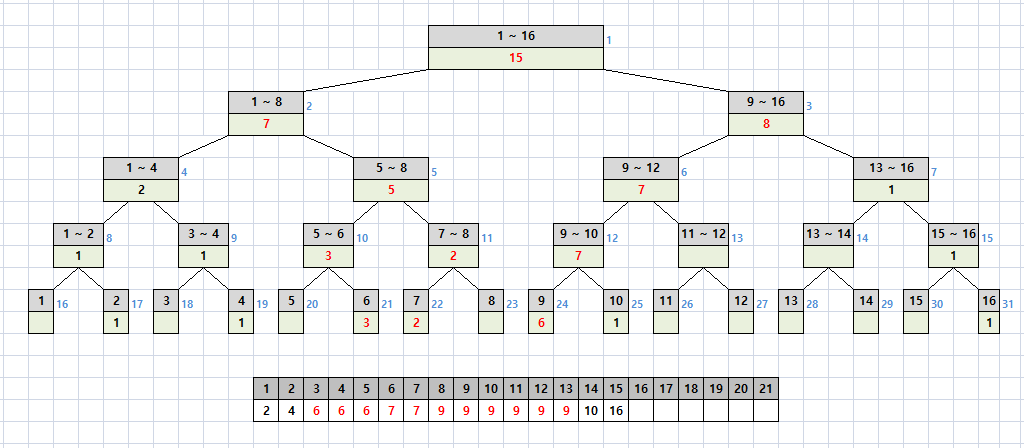
2, 4, 6, 6, 6, 7, 7, 9, 9, 9, 9, 9, 9, 10, 16에서 가운데 값은 8번째에 있는 9가 된다.
위에서 한 방법으로 정답인 9가 나오는지 확인해보자.
(1) treeIdx = 1, index = 8이고
8 <= tree[treeIdx * 2] = 7을 만족하지 않으므로, treeIdx = 1 * 1 + 1 = 3이 되고, index -= 7로 1이 된다.
(2) treeIdx = 3, index = 1이고
1 <= tree[treeIdx * 2] = 7을 만족하므로, treeIdx = 6이 된다.
(3) treeIdx = 6, index = 1이고
1 <= tree[treeIdx * 2] = 7을 만족하므로, treeIdx = 12가 된다.
(4) treeIdx = 12, index = 1이고
1 <= tree[treeIdx * 2] = 6을 만족하므로, treeIdx = 24가 된다.
따라서 treeIdx - 15 = 9를 찾을 수 있게 된다.
구현 - Bottom-Up Segment Tree
Bottom-Up 트리로 구현해보자.
주어지는 수가 -10,000 ~ 10,000이기 때문에 10,001을 더해 1 ~ 20,001로 바꾸고,
답을 구할 때는 다시 10,001을 뺀다.
총 2만개의 leaf가 필요하므로 2만개보다 큰 2의 배수의 수는 32,768이므로,
tree의 size는 두 배 큰 65,536이 된다.
Bottom-Up에서 start는 65,536의 절반에 1을 뺀 값이다.
그리고 위에 설명한 방식으로 정답을 찾을 때, 마지막 leaf의 개수까지 반복하므로 leafSize = 32,768로 잡는다.
위에서 정답을 찾는 과정을 함수로 구현하면 아래와 같다.
int getMid(int index)
{
int treeIdx = 1;
while (treeIdx < leafSize)
{
if (index <= tree[treeIdx * 2]) treeIdx *= 2;
else
{
index -= tree[treeIdx * 2];
treeIdx = treeIdx * 2 + 1;
}
}
return treeIdx - start;
}
입력을 받은 값에 MID를 더해서 update하고, getMid에서 찾을 index는 i가 주어질 때, (i + 1) / 2번째 값을 찾는다.
전체 수가 짝수 개인 경우는 중간의 수 중 작은 값을 찾으라고 했기 때문이다.
전체 코드는 다음과 같다.
#include <stdio.h>
#define MID (10001)
#define MAX (20010)
int N;
int tree[65536]; // 2^16
int start, leafSize;
void update(int index, int diff)
{
index += start;
while (index > 1)
{
tree[index] += diff;
index /= 2;
}
}
int getMid(int index)
{
int treeIdx = 1;
while (treeIdx < leafSize)
{
if (index <= tree[treeIdx * 2]) treeIdx *= 2;
else
{
index -= tree[treeIdx * 2];
treeIdx = treeIdx * 2 + 1;
}
}
return treeIdx - start;
}
void showSegment(int size)
{
for (int i = 1; i <= size; i <<= 1)
{
for (int k = i; k <= (i << 1) - 1; k++)
printf("%d ", tree[k]);
putchar('\n');
}
putchar('\n');
}
int main()
{
scanf("%d", &N);
start = 32768 - 1;
leafSize = 32768;
for (int i = 1; i <= N; i++)
{
int value;
scanf("%d", &value);
update(value + MID, 1);
printf("%d\n", getMid((i + 1) / 2) - MID);
}
return 0;
}구현 - Top-Down Segment Tree
Top-Down 방식은 다음과 같다.
#include <stdio.h>
#define MID (10001)
#define MAX (20001)
int N;
int tree[65536]; // 2^16
void update(int left, int right, int node, int index, int diff)
{
if (index < left || right < index) return;
tree[node] += diff;
if (left != right)
{
int mid = (left + right) / 2;
update(left, mid, node * 2, index, diff);
update(mid + 1, right, node * 2 + 1, index, diff);
}
}
int getMid(int left, int right, int node, int value)
{
if (left == right) return left;
int mid = (left + right) / 2;
if (value <= tree[node * 2]) return getMid(left, mid, node * 2, value);
else return getMid(mid + 1, right, node * 2 + 1, value -= tree[node * 2]);
}
int main()
{
scanf("%d", &N);
for (int i = 1; i <= N; i++)
{
int value;
scanf("%d", &value);
update(1, MAX, 1, value + MID, 1);
printf("%d\n", getMid(1, MAX, 1, (i + 1) / 2) - MID);
}
return 0;
}구현 - Dynamic Segment Tree
다이나믹 세그먼트 트리 방식은 다음과 같다.
#include <stdio.h>
#define MID (10001)
#define MAX (20001)
struct NODE
{
int value;
int left;
int right;
};
int N;
NODE tree[65536]; // 2^16
int tcnt = 2;
void update(int left, int right, int node, int index, int diff)
{
if (index < left || right < index) return;
tree[node].value += diff;
if (left == right) return;
if (tree[node].left == 0) tree[node].left = tcnt++;
if (tree[node].right == 0) tree[node].right = tcnt++;
int mid = (left + right) / 2;
int leftNodeIndex = tree[node].left;
int rightNodeIndex = tree[node].right;
update(left, mid, leftNodeIndex, index, diff);
update(mid + 1, right, rightNodeIndex, index, diff);
}
int getMid(int left, int right, int node, int value)
{
if (left == right) return left;
int mid = (left + right) / 2;
int leftNodeIndex = tree[node].left;
int rightNodeIndex = tree[node].right;
if (value <= tree[leftNodeIndex].value) return getMid(left, mid, leftNodeIndex, value);
else return getMid(mid + 1, right, rightNodeIndex, value -= tree[leftNodeIndex].value);
}
int main()
{
scanf("%d", &N);
for (int i = 1; i <= N; i++)
{
int value;
scanf("%d", &value);
update(1, MAX, 1, value + MID, 1);
printf("%d\n", getMid(1, MAX, 1, (i + 1) / 2) - MID);
}
return 0;
}