알고리즘/BAEKJOON
BOJ 1708 : 볼록 껍질
피로물든딸기
2022. 12. 28. 20:00
반응형
https://www.acmicpc.net/problem/1708
참고
- 스택
- 머지 소트
- 컨벡스 헐로 볼록 다각형을 만드는 점의 좌표 구하기
- 컨벡스 헐로 임의의 점을 모두 포함하는 사각형 구하기

점의 좌표가 주어졌을 때, 볼록 다각형을 만드는 점의 개수를 구해보자.
볼록 다각형을 찾는 컨벡스 헐 알고리즘(Convex Hull Algorithm)은 스택을 이용한다.
먼저 주어진 점에서 가장 작은 (x, y) 좌표를 찾는다.
for (int i = 0; i < N; i++)
{
scanf("%lld %lld", &a[i].x, &a[i].y);
if (minXY.y >= a[i].y) // 가장 작은 y, x 좌표를 찾는다.
{
if (minXY.y == a[i].y)
{
if (minXY.x > a[i].x)
{
minXY.x = a[i].x;
minXY.y = a[i].y;
}
}
else
{
minXY.x = a[i].x;
minXY.y = a[i].y;
}
}
}
그리고 이 점을 기준으로 counter clock wise (= ccw) 알고리즘을 이용하여 반시계 방향이 되도록 정렬하고,
같은 방향이라면 더 짧은 방향의 좌표를 기준으로 정렬한다.
정렬은 merge sort를 이용하였다.
typedef struct st
{
ll x;
ll y;
}XY;
ll ccw(XY A, XY B, XY C)
{
XY v1, v2;
v1.x = B.x - A.x;
v1.y = B.y - A.y;
v2.x = C.x - A.x;
v2.y = C.y - A.y;
return v1.x * v2.y - v2.x * v1.y;
}
ll length(XY a, XY b)
{
return (a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y);
}
int minV(XY a, XY b)
{
ll tmp = ccw(minXY, a, b);
if (tmp > 0) return 1;
else if (tmp == 0 && (length(minXY, a) < length(minXY, b))) return 1;
return 0;
}
void merge(int start, int end)
{
int mid, i, j, k;
mid = (start + end) / 2;
i = start;
j = mid + 1;
k = 0;
while (i <= mid && j <= end)
{
if (minV(a[i], a[j])) b[k++] = a[i++];
else b[k++] = a[j++];
}
while (i <= mid) b[k++] = a[i++];
while (j <= end) b[k++] = a[j++];
for (i = start; i <= end; i++)
a[i] = b[i - start];
}
반시계 방향이 되는 경우 최대 3개까지 스택에 넣는다.
직선이 되는 경우는 최근의 점으로 stack에서 좌표를 빼고 다시 넣는다.
while (sp < 3)
{
ll tmp = ccw(stack[sp - 2], stack[sp - 1], a[cnt]);
if (tmp > 0) stack[sp++] = a[cnt++];
else if (tmp == 0) // 직선인 경우는 점을 교체
{
sp--;
stack[sp++] = a[cnt++];
}
else cnt++;
}
이제 stack의 가장 위에 있는 2개의 점과 다음 점을 비교한다.
반시계방향이면 좌표를 추가하고, 그렇지 않다면 좌표를 제거한다.
while (cnt < N)
{
ll tmp = ccw(stack[sp - 2], stack[sp - 1], a[cnt]);
if (tmp > 0) stack[sp++] = a[cnt++];
else sp--;
}
위와 같이 평면상에서 유한한 점들의 볼록 껍질(다각형)을 찾는 방법을 그레이엄 스캔(Graham's Scan)이라고 한다.
이 과정을 유니티 - 볼록 다각형을 만드는 점의 좌표 구하기에 응용한 결과를 보면 다음과 같이 다각형을 만든다.
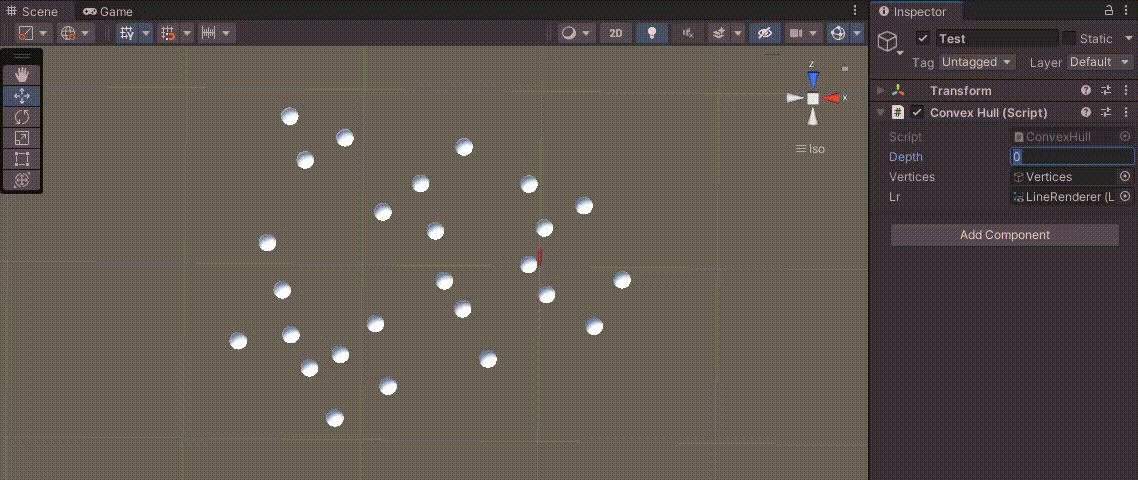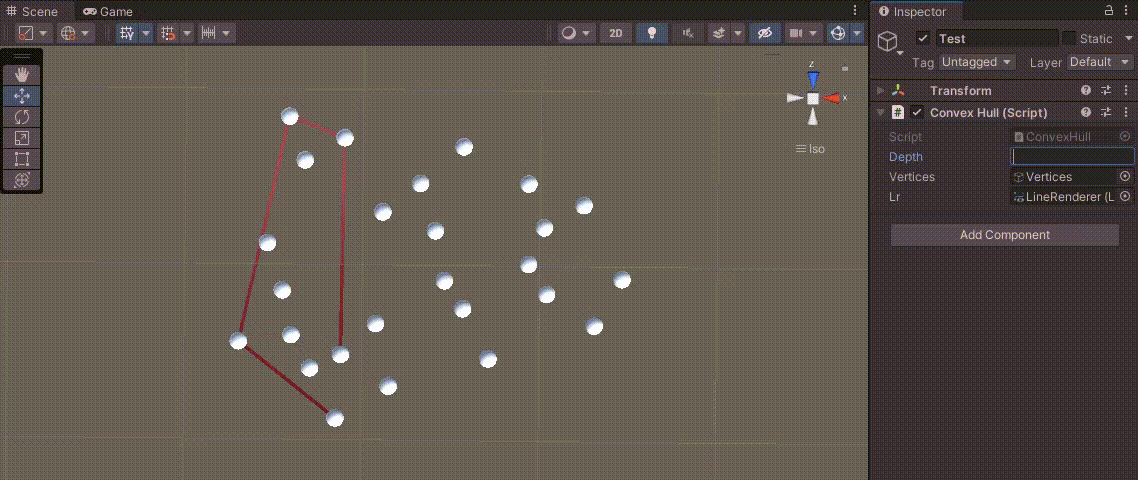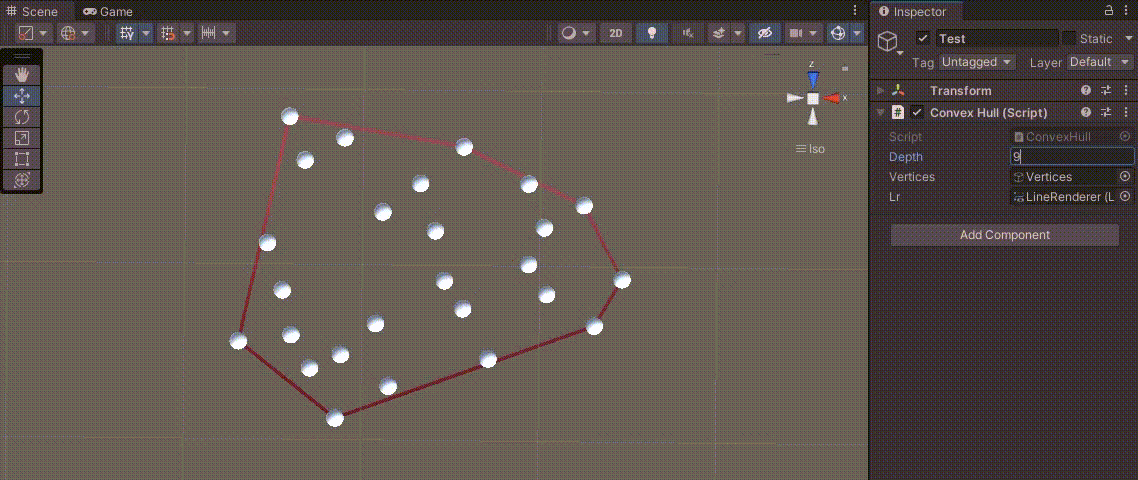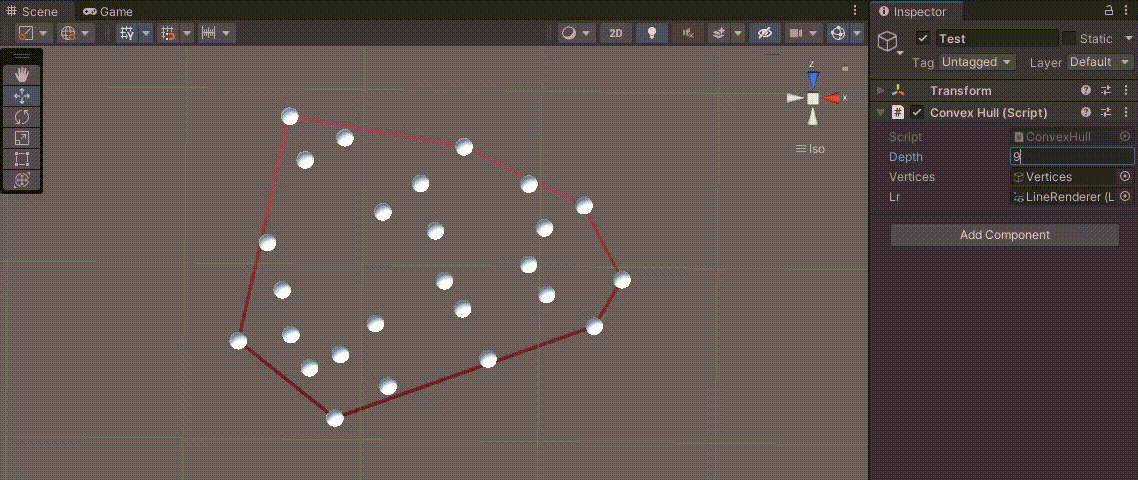
전체 코드는 다음과 같다.
#include <stdio.h>
typedef long long int ll;
int N;
typedef struct st
{
ll x;
ll y;
}XY;
XY a[100100];
XY b[100100];
XY stack[100100];
int sp;
XY minXY;
ll ccw(XY A, XY B, XY C)
{
XY v1, v2;
v1.x = B.x - A.x;
v1.y = B.y - A.y;
v2.x = C.x - A.x;
v2.y = C.y - A.y;
return v1.x * v2.y - v2.x * v1.y;
}
ll length(XY a, XY b)
{
return (a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y);
}
int minV(XY a, XY b)
{
ll tmp = ccw(minXY, a, b);
if (tmp > 0) return 1;
else if (tmp == 0 && (length(minXY, a) < length(minXY, b))) return 1;
return 0;
}
void merge(int start, int end)
{
int mid, i, j, k;
mid = (start + end) / 2;
i = start;
j = mid + 1;
k = 0;
while (i <= mid && j <= end)
{
if (minV(a[i], a[j])) b[k++] = a[i++];
else b[k++] = a[j++];
}
while (i <= mid) b[k++] = a[i++];
while (j <= end) b[k++] = a[j++];
for (i = start; i <= end; i++)
a[i] = b[i - start];
}
void sort(int start, int end)
{
int mid;
if (start == end) return;
mid = (start + end) / 2;
sort(start, mid);
sort(mid + 1, end);
merge(start, end);
}
int main(void)
{
int cnt;
scanf("%d", &N);
minXY.x = minXY.y = 0x7fff0000;
for (int i = 0; i < N; i++)
{
scanf("%lld %lld", &a[i].x, &a[i].y);
if (minXY.y >= a[i].y) // 가장 작은 y, x 좌표를 찾는다.
{
if (minXY.y == a[i].y)
{
if (minXY.x > a[i].x)
{
minXY.x = a[i].x;
minXY.y = a[i].y;
}
}
else
{
minXY.x = a[i].x;
minXY.y = a[i].y;
}
}
}
sort(0, N - 1);
cnt = 0;
stack[sp++] = a[cnt++];
stack[sp++] = a[cnt++];
while (sp < 3)
{
ll tmp = ccw(stack[sp - 2], stack[sp - 1], a[cnt]);
if (tmp > 0) stack[sp++] = a[cnt++];
else if (tmp == 0) // 직선인 경우는 점을 교체
{
sp--;
stack[sp++] = a[cnt++];
}
else cnt++;
}
while (cnt < N)
{
ll tmp = ccw(stack[sp - 2], stack[sp - 1], a[cnt]);
if (tmp > 0) stack[sp++] = a[cnt++];
else sp--;
}
printf("%d\n", sp);
return 0;
}
이 문제는 볼록 다각형을 만드는 점의 좌표의 개수를 구하는 문제다.
볼록 다각형을 만드는 점의 좌표는 알고리즘 종료 후 스택에 모두 저장되어 있다.
반응형