[코드트리] 코드트리 DB (삼성 SW 역량테스트 2024 하반기 오전 2번, B형)
SW 역량테스트 합격하기 A형 강의 오픈!! (인프런 바로가기)

삼성 A형 전체 링크
삼성 B형 전체 링크
2022 하반기 이후 문제 풀이 시간이 3시간 → 4시간으로 변경,
A형 1문제 + B형 문제 1문제가 출제됩니다.
참고
- 산타의 선물 공장
- 구간 합 구하기 with 탑 다운 세그먼트 트리 (Top-Down Segment Tree)
- 구간 합 구하기 with 다이나믹 세그먼트 트리 (Dynamic Segment Tree)
- BOJ 1655 : 가운데를 말해요 with 세그먼트 트리
https://www.codetree.ai/training-field/frequent-problems/problems/codetree-db
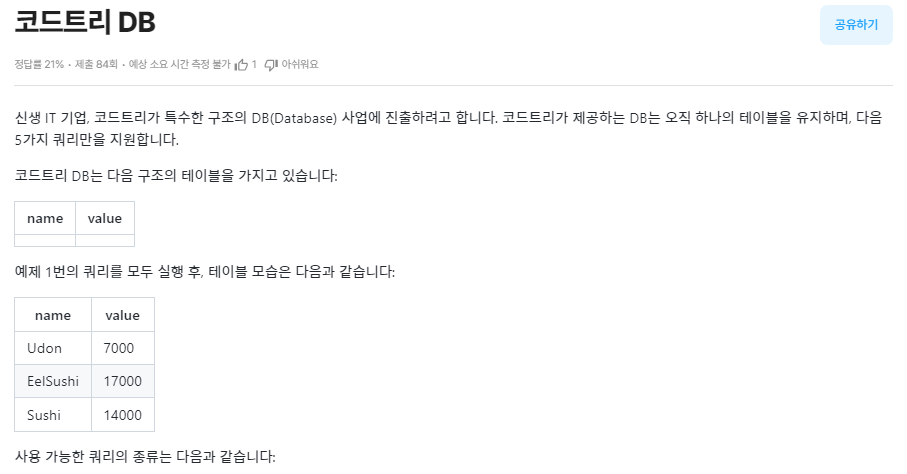
문제를 요약하면 다음과 같다.
init
- 테이블을 초기화 한다.
테이블은 unorderd_map으로 관리하고, 그 외 쿼리는 세그먼트 트리를 이용하면 된다.
따라서 unordered_map과 세그먼트 트리를 초기화하면 된다.
insert
- 테이블에 새로운 데이터를 추가한다.
unordered_map과 세그먼트 트리에 값을 추가하면 된다.
delete
- 테이블에서 데이터를 삭제한다.
unordered_map과 세그먼트 트리에 값을 삭제하면 된다.
rank
- 테이블에서 k번째로 작은 value를 가진 데이터를 조회한다.
k가 주어진 data의 개수보다 큰 경우 None을 리턴해야 된다.
그래서 insert가 성공할 경우 dataCount를 증가하고, delete가 성공할 경우 dataCount를 감소한다.
sum
- 테이블에서 특정 값 이하의 value를 가진 데이터들의 합을 계산한다.
세그먼트 트리에서 구간의 합을 리턴하면 된다.
다이나믹 세그먼트 트리
구간의 합을 구하려면 세그먼트 트리를 사용하면 된다.
이때, 주어지는 value의 값이 최대 1,000,000,000이라서 일반적인 세그먼트 트리로는 메모리가 부족하다.
하지만 insert 쿼리는 최대 100,000번만 주어진다.
따라서 필요한 만큼만 메모리를 사용할 수 있는 다이나믹 세그먼트 트리를 사용하면 된다.
log2(1,000,000,000)은 약 30이고, 10만 번 insert가 발생하므로, 메모리는 약 300만 정도가 필요하다.
#define MAX (3000000 + 10000) // log2(1000000000) * 10만번 insert
세그먼트 트리는 다음의 구조체를 이용해서 선언한다.
value가 추가되면 NODE의 index는 1이 되고, value가 삭제되면 index는 0이 된다.
left와 right는 다이나믹 세그먼트 트리를 사용하기 위한 변수다.
입력될 값은 int 형이고, 구간의 합은 최대 int보다 크기 때문에 sum은 long long int로 선언하였다.
typedef long long int ll;
struct NODE
{
int index;
int left;
int right;
ll sum;
};
NODE tree[MAX];
int tcnt;
rank 쿼리에서는 k번째의 값이 무엇인지 알아야 하고, sum에서는 구간의 합을 구해야 한다.
어떤 값이 몇 번째에 있는지는 가운데를 말해요에서 세그먼트 트리로 value를 index로 관리하면 된다.
즉, value가 insert / delete 되면 update 함수를 이용해 해당되는 구간의 value를 +1 / -1 로 갱신한다.
그런데 sum 쿼리에서는 구간의 합을 구해야 되므로, Node의 sum에는 index를 곱해서 더하면 된다.
void update(int left, int right, int node, int index, int diff)
{
if (index < left || right < index) return;
tree[node].index += diff;
if (left == right)
{
tree[node].sum = (index * tree[node].index);
return;
}
if (tree[node].left == 0) tree[node].left = tcnt++;
if (tree[node].right == 0) tree[node].right = tcnt++;
int mid = (left + right) / 2;
int leftNodeIndex = tree[node].left;
int rightNodeIndex = tree[node].right;
update(left, mid, leftNodeIndex, index, diff);
update(mid + 1, right, rightNodeIndex, index, diff);
tree[node].sum = (tree[leftNodeIndex].sum) + (tree[rightNodeIndex].sum);
}
k번째 값은 getValue를 이용해서 구하면 된다.
int getValue(int left, int right, int node, int value)
{
if (node == 0) return 0;
if (left == right) return left;
int mid = (left + right) / 2;
int leftNodeIndex = tree[node].left;
int rightNodeIndex = tree[node].right;
if (value <= tree[leftNodeIndex].index) return getValue(left, mid, leftNodeIndex, value);
else return getValue(mid + 1, right, rightNodeIndex, value -= tree[leftNodeIndex].index);
}
구간의 합은 getSum을 이용해서 구하면 된다.
ll getSum(int left, int right, int a, int b, int node)
{
if (node == 0) return 0;
if (b < left || right < a) return 0;
if (a <= left && right <= b) return tree[node].sum;
int mid = (left + right) / 2;
return
getSum(left, mid, a, b, tree[node].left) + getSum(mid + 1, right, a, b, tree[node].right);
}unordered_map
테이블에 value와 name이 삽입되면 unordere_map에 기록해서 존재하는 value와 name을 즉시 구할 수 있다.
unordered_map은 산타의 선물 공장을 참고하면 된다.
init
unordered_map, dataCount, tree를 모두 초기화하면 된다.
void init()
{
nameToValue.clear();
valueToName.clear();
dataCount = 0;
tcnt = 2;
for (int i = 0; i < MAX; i++)
tree[i].left = tree[i].right = tree[i].value = tree[i].sum = 0;
}insert
주어진 name과 value가 unordered_map에 존재하는 경우는 0을 리턴한다.
그렇지 않다면 unordered_map에 값을 추가하고, dataCount를 1 증가시킨다.
그리고 세그먼트 트리에 해당되는 value를 +1로 update 하면 된다.
int insertDB(string name, int value)
{
if (nameToValue.count(name) != 0 || valueToName.count(value) != 0)
return 0;
nameToValue[name] = value;
valueToName[value] = name;
dataCount++;
update(1, MAX_VALUE, 1, value, 1);
return 1;
}delete
존재하지 않는 name이라면 0을 리턴하면 된다.
그리고 name을 unordered_map에 넣어서 value를 얻는다.
name과 value를 테이블에서 삭제하고 dataCount는 1 감소한다.
그리고 세그먼트 트리에 해당되는 value를 -1로 update 하여 0으로 만들면 된다.
int deleteDB(string name)
{
if (nameToValue.count(name) == 0) return 0;
int value = nameToValue[name];
nameToValue.erase(name);
valueToName.erase(value);
dataCount--;
update(1, MAX_VALUE, 1, value, -1);
return value;
}rank
insert와 delete에서 data의 개수를 dataCount로 카운팅 하고 있으므로,
dataCount보다 k가 큰 경우는 None을 리턴하면 된다.
k에 해당하는 value는 getValue를 이용해서 구하면 되고,
unordere_map에 value로 name을 구할 수 있다.
string rankDB(int k)
{
if (dataCount < k) return "None";
int value = getValue(1, MAX_VALUE, 1, k);
string name = valueToName[value];
return name;
}sum
세그먼트 트리에서 1부터 k까지 구간의 합을 구하면 된다.
ll sumDB(int k)
{
return getSum(1, MAX_VALUE, 1, k, 1);
}전체 코드는 다음과 같다.
#include <stdio.h>
#include <string>
#include <iostream>
#include <unordered_map>
#define MAX (3000000 + 10000) // log2(1000000000) * 10만번 insert
#define MAX_VALUE (1000000000)
using namespace std;
typedef long long int ll;
int Q;
unordered_map<string, int> nameToValue;
unordered_map<int, string> valueToName;
int dataCount;
struct NODE
{
int index;
int left;
int right;
ll sum;
};
NODE tree[MAX];
int tcnt;
void update(int left, int right, int node, int index, int diff)
{
if (index < left || right < index) return;
tree[node].index += diff;
if (left == right)
{
tree[node].sum = (index * tree[node].index);
return;
}
if (tree[node].left == 0) tree[node].left = tcnt++;
if (tree[node].right == 0) tree[node].right = tcnt++;
int mid = (left + right) / 2;
int leftNodeIndex = tree[node].left;
int rightNodeIndex = tree[node].right;
update(left, mid, leftNodeIndex, index, diff);
update(mid + 1, right, rightNodeIndex, index, diff);
tree[node].sum = (tree[leftNodeIndex].sum) + (tree[rightNodeIndex].sum);
}
int getValue(int left, int right, int node, int value)
{
if (node == 0) return 0;
if (left == right) return left;
int mid = (left + right) / 2;
int leftNodeIndex = tree[node].left;
int rightNodeIndex = tree[node].right;
if (value <= tree[leftNodeIndex].index) return getValue(left, mid, leftNodeIndex, value);
else return getValue(mid + 1, right, rightNodeIndex, value -= tree[leftNodeIndex].index);
}
ll getSum(int left, int right, int a, int b, int node)
{
if (node == 0) return 0;
if (b < left || right < a) return 0;
if (a <= left && right <= b) return tree[node].sum;
int mid = (left + right) / 2;
return
getSum(left, mid, a, b, tree[node].left) + getSum(mid + 1, right, a, b, tree[node].right);
}
void init()
{
nameToValue.clear();
valueToName.clear();
dataCount = 0;
tcnt = 2;
for (int i = 0; i < MAX; i++)
tree[i].left = tree[i].right = tree[i].index = tree[i].sum = 0;
}
int insertDB(string name, int value)
{
if (nameToValue.count(name) != 0 || valueToName.count(value) != 0)
return 0;
nameToValue[name] = value;
valueToName[value] = name;
dataCount++;
update(1, MAX_VALUE, 1, value, 1);
return 1;
}
int deleteDB(string name)
{
if (nameToValue.count(name) == 0) return 0;
int value = nameToValue[name];
nameToValue.erase(name);
valueToName.erase(value);
dataCount--;
update(1, MAX_VALUE, 1, value, -1);
return value;
}
string rankDB(int k)
{
if (dataCount < k) return "None";
int value = getValue(1, MAX_VALUE, 1, k);
string name = valueToName[value];
return name;
}
ll sumDB(int k)
{
return getSum(1, MAX_VALUE, 1, k, 1);
}
int main()
{
scanf("%d", &Q);
for (int q = 0; q < Q; q++)
{
string command, name;
int value;
cin >> command;
if (command == "init") init();
else if (command == "insert")
{
cin >> name >> value;
cout << insertDB(name, value) << endl;
}
else if (command == "delete")
{
cin >> name;
cout << deleteDB(name) << endl;
}
else if (command == "rank")
{
cin >> value;
cout << rankDB(value) << endl;
}
else if (command == "sum")
{
cin >> value;
cout << sumDB(value) << endl;
}
}
return 0;
}